- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основы графической визуализации данных. Трехмерный случай
Содержание
- 2. Создание матриц для построения 3D графиковДля создания
- 3. CreateSpaceCreateSpace(F(или fI, f2, f3) , t0,t1,tgrid,fmap) – создание
- 4. Пример использования функции CreateSpaceЗаметьте, для построения графика кривой
- 5. CreateMesh(F (или g, или f1,f2,f3),s0,s1,t0,t1,sgrid,tgrid, fmap) – создание вложенного
- 6. Результатом обеих рассмотренных функций CreateMesh и CreateSpace является соответствующий вложенный массив,
- 7. Скачать презентацию
- 8. Похожие презентации
Создание матриц для построения 3D графиковДля создания матриц имеются еще две специфические функции, применяемые, в основном, для быстрого и эффектного представления каких-либо зависимостей в виде трехмерных графиков (типа поверхности или пространственной кривой). Все их аргументы, кроме





Слайд 3
CreateSpace
CreateSpace(F(или fI, f2, f3) , t0,t1,tgrid,fmap) – создание вложенного
массива, представляющего х-, у- и z-координаты параметрической пространственной кривой,
заданной функцией F:F(t) – векторная функция из трех элементов, заданная параметрически относительно единственного аргумента
t;f1(t),f2 (t), f3 (t) – скалярные функции;
t0 – нижний предел t (по умолчанию -5);
t1 – верхний предел t (по умолчанию 5);
tgrid – число точек сетки по переменной t (по умолчанию 20);
fmap – векторная функция от трех аргументов, задающая преобразование координат.
Слайд 4
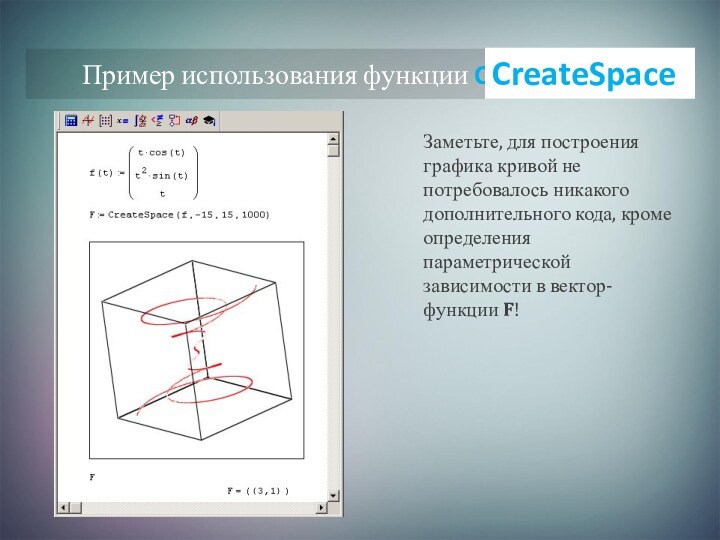
Пример использования функции CreateSpace
Заметьте, для построения графика кривой не
потребовалось никакого дополнительного кода, кроме определения параметрической зависимости в
вектор-функции F!CreateSpace
Слайд 5 CreateMesh(F (или g, или f1,f2,f3),s0,s1,t0,t1,sgrid,tgrid, fmap) – создание вложенного массива,
представляющего х-, у- и z-координаты параметрической поверхности, заданной функцией F:
F(s,t) –
векторная функция из трех элементов, заданная параметрически относительно двух аргументов s и t;g (s, t) – скалярная функция;
f1(s,t),f2 (s,t),f3(s,t) – скалярные функции;
s0, t0 – нижние пределы аргументов s,t (по умолчанию -5);
s1,t1 – верхние пределы аргументов s,t (по умолчанию 5);
sgrid, tgrid – число точек сетки по переменным s и t (по умолчанию 20);
fmap – векторная функция из трех элементов от трех аргументов, задающая преобразование координат.
CreateMesh
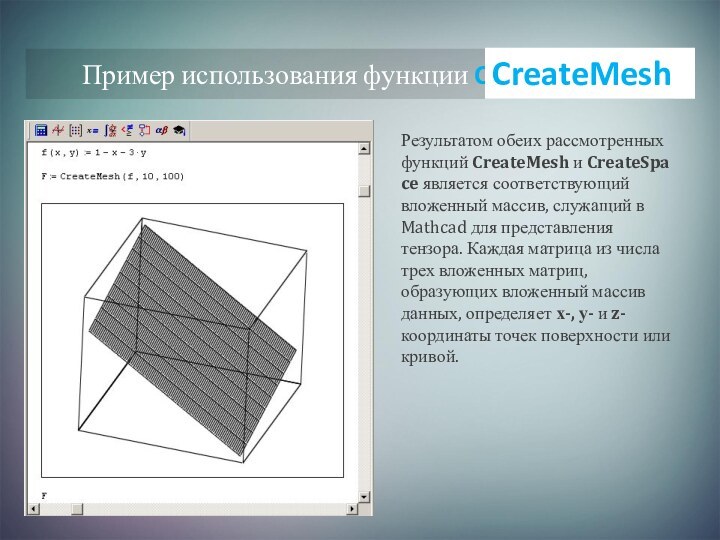
Слайд 6 Результатом обеих рассмотренных функций CreateMesh и CreateSpace является соответствующий вложенный массив, служащий
в Mathcad для представления тензора. Каждая матрица из числа
трех вложенных матриц, образующих вложенный массив данных, определяет х-, у- и z-координаты точек поверхности или кривой.Пример использования функции CreateSpace
CreateMesh