- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Подготовка данных. Факторный анализ
Содержание
- 2. НормализацияДесятичное масштабированиеМинимаксная нормализацияНормализация с помощью стандартного преобразованияНормализация с помощью поэлементных преобразований
- 3. Десятичное масштабирование
- 4. Минимаксная нормализация
- 5. Нормализация с помощью стандартного отклонения
- 6. Нормализация с помощью поэлементных преобразований
- 7. Факторный анализФакторный анализ (ФА) представляет собой совокупность
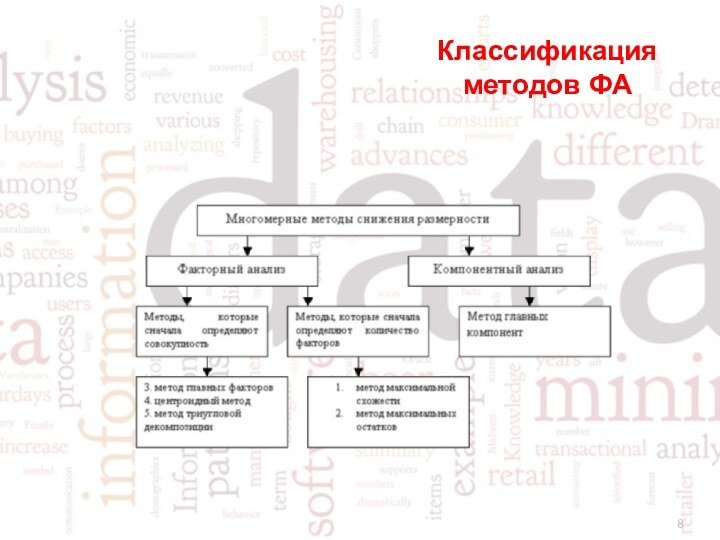
- 8. Классификация методов ФА
- 9. Метод главных компонентМетод главных компонент (МГК) применяется для снижения
- 10. Метод главных компонент. Схема
- 11. Метод главных компонент. Матрица счетовМатрица счетов T дает нам
- 12. Метод главных компонент. Матрица нагрузокМатрица нагрузок P – это
- 13. Особенности метода главных компонентВ основе метода главных
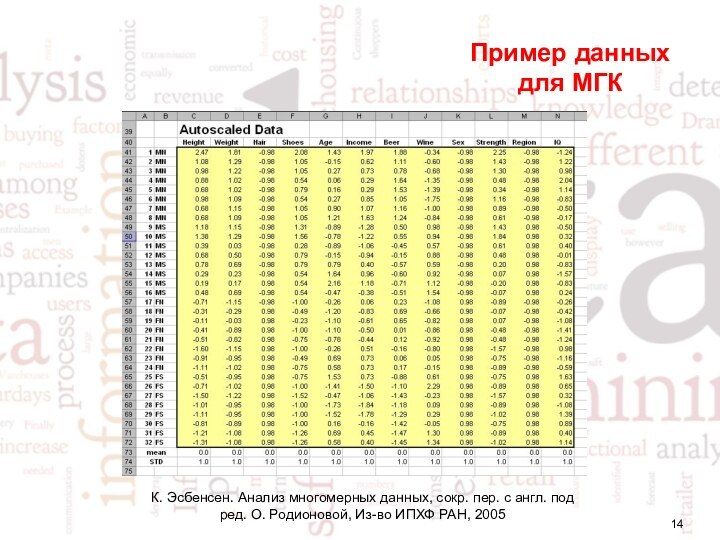
- 14. Пример данных для МГКК. Эсбенсен. Анализ многомерных данных,
- 15. Пример данных для МГК. Обозначения
- 16. Матрица счетов
- 17. Матрица нагрузок
- 18. Объекты выборки в пространстве новых компонентЖенщины (F)
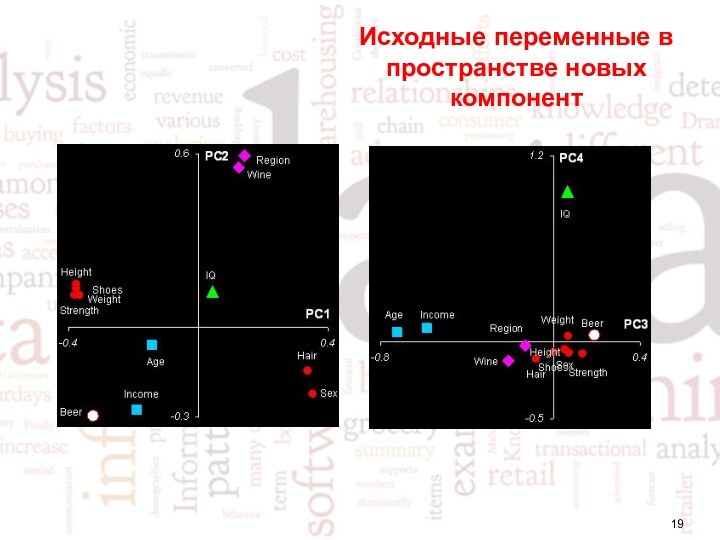
- 19. Исходные переменные в пространстве новых компонент
- 20. График «каменистой осыпи» (scree plot)
- 21. Метод главных факторовВ парадигме метода главных факторов
- 22. Вращение факторовВращение - это способ превращения факторов,
- 23. Ортогональное вращениеОртогональное вращение подразумевает, что мы будем
- 24. Варимаксное вращениеЭтот критерий использует формализацию сложности фактора
- 25. Квартимаксное вращениеФормализуем понятие факторной сложности q i-ой
- 26. Критерии определения числа факторовГлавной проблемой факторного анализа
- 27. Критерии определения числа факторов. ПродолжениеКритерий значимости. Он
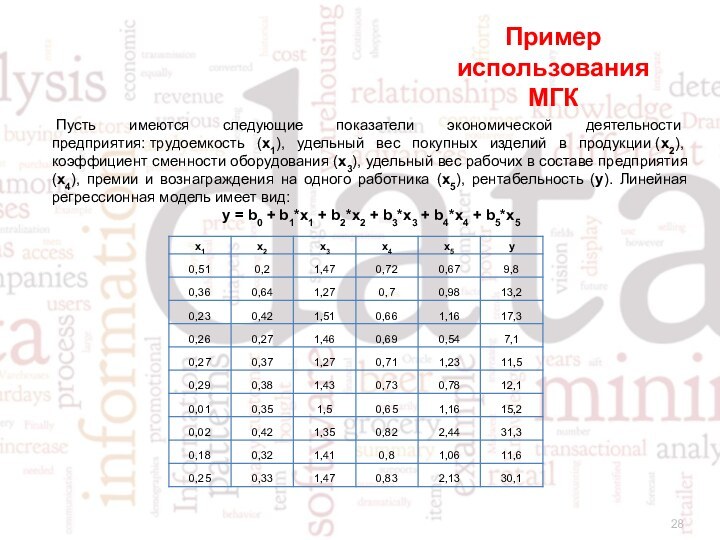
- 28. Пример использования МГК Пусть имеются следующие показатели экономической
- 29. Пример использования МГКПостроение регрессионной модели в статистическом
- 30. Пример использования МГККритерий Кайзера для МГК показывает,
- 31. Пример использования МГКТеперь можно построить в новых
- 32. Метод сингулярного разложения (SVD)Beltrami и Jordan считаются
- 33. Скачать презентацию
- 34. Похожие презентации


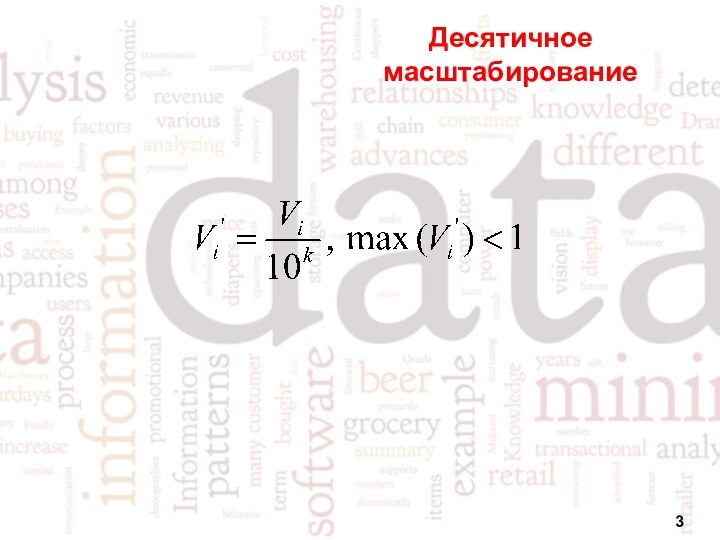























Слайд 2
Нормализация
Десятичное масштабирование
Минимаксная нормализация
Нормализация с помощью стандартного преобразования
Нормализация с
помощью поэлементных преобразований
Слайд 7
Факторный анализ
Факторный анализ (ФА) представляет собой совокупность методов,
которые на основе реально существующих связей анализируемых признаков, связей
самих наблюдаемых объектов, позволяют выявлять скрытые (неявные, латентные) обобщающие характеристики организационной структуры и механизма развития изучаемых явлений, процессов.Методы факторного анализа в исследовательской практике применяются главным образом с целью сжатия информации, получения небольшого числа обобщающих признаков, объясняющих вариативность (дисперсию) элементарных признаков (R-техника факторного анализа) или вариативность наблюдаемых объектов (Q-техника факторного анализа).
Алгоритмы факторного анализа основываются на использовании редуцированной матрицы парных корреляций (ковариаций). Редуцированная матрица – это матрица, на главной диагонали которой расположены не единицы (оценки) полной корреляции или оценки полной дисперсии, а их редуцированные, несколько уменьшенные величины. При этом постулируется, что в результате анализа будет объяснена не вся дисперсия изучаемых признаков (объектов), а ее некоторая часть, обычно большая. Оставшаяся необъясненная часть дисперсии — это характерность, возникающая из-за специфичности наблюдаемых объектов, или ошибок, допускаемых при регистрации явлений, процессов, т.е. ненадежности вводных данных.
Слайд 9
Метод главных компонент
Метод главных компонент (МГК) применяется для снижения размерности
пространства наблюдаемых векторов, не приводя к существенной потере информативности. Предпосылкой
МГК является нормальный закон распределения многомерных векторов. В МГК линейные комбинации случайных величин определяются характеристическими векторами ковариационной матрицы. Главные компоненты представляют собой ортогональную систему координат, в которой дисперсии компонент характеризуют их статистические свойства. МГК не относят к ФА, хотя он имеет схожий алгоритм и решает схожие аналитические задачи. Его главное отличие заключается в том, что обработке подлежит не редуцированная, а обычная матрица парных корреляций, ковариаций, на главной диагонали которой расположены единицы.Пусть дан исходный набор векторов X линейного пространства Lk. Применение метода главных компонент позволяет перейти к базису пространства Lm (m≤k), такому что: первая компонента (первый вектор базиса) соответствует направлению, вдоль которого дисперсия векторов исходного набора максимальна. Направление второй компоненты (второго вектора базиса) выбрано таким образом, чтобы дисперсия исходных векторов вдоль него была максимальной при условии ортогональности первому вектору базиса. Аналогично определяются остальные векторы базиса. В результате, направления векторов базиса выбраны так, чтобы максимизировать дисперсию исходного набора вдоль первых компонент, называемых главными компонентами (или главными осями).Получается, что основная изменчивость векторов исходного набора векторов представлена несколькими первыми компонентами, и появляется возможность, отбросив менее существенные компоненты, перейти к пространству меньшей размерности.
Слайд 11
Метод главных компонент. Матрица счетов
Матрица счетов T дает нам проекции
исходных образцов (J –мерных векторов x1,…,xI) на подпространство главных компонент (A-мерное).
Строки t1,…,tI матрицы T – это координаты образцов в новой системе координат. Столбцы t1,…,tA матрицы T – ортогональны и представляют проекции всех образцов на одну новую координатную ось.При исследовании данных методом PCA, особое внимание уделяется графикам счетов. Они несут в себе информацию, полезную для понимания того, как устроены данные. На графике счетов каждый образец изображается в координатах (ti, tj), чаще всего – (t1, t2), обозначаемых PC1 и PC2. Близость двух точек означает их схожесть, т.е. положительную корреляцию. Точки, расположенные под прямым углом, являются некоррелироваными, а расположенные диаметрально противоположно – имеют отрицательную корреляцию.
Слайд 12
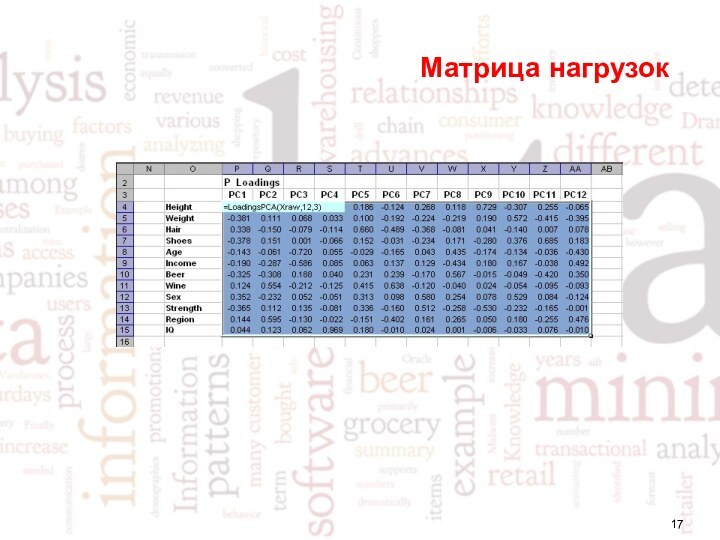
Метод главных компонент. Матрица нагрузок
Матрица нагрузок P – это матрица
перехода из исходного пространства переменных x1, …xJ (J-мерного) в пространство главных
компонент (A-мерное). Каждая строка матрицы P состоит из коэффициентов, связывающих переменные t и x. Например, a-я строка – это проекция всех переменных x1, …xJ на a-ю ось главных компонент. Каждый столбец P – это проекция соответствующей переменной xj на новую систему координат.График нагрузок применяется для исследования роли переменных. На этом графике каждая переменная xj отображается точкой в координатах (pi, pj), например (p1, p2). Анализируя его аналогично графику счетов, можно понять, какие переменные связаны, а какие независимы. Совместное исследование парных графиков счетов и нагрузок, также может дать много полезной информации о данных.
Слайд 13
Особенности метода главных компонент
В основе метода главных компонент
лежат следующие допущения:
допущение о том, что размерность данных может
быть эффективно понижена путем линейного преобразования;допущение о том, что больше всего информации несут те направления, в которых дисперсия входных данных максимальна.
Можно легко видеть, что эти условия далеко не всегда выполняются. Например, если точки входного множества располагаются на поверхности гиперсферы, то никакое линейное преобразование не сможет понизить размерность (но с этим легко справится нелинейное преобразование, опирающееся на расстояние от точки до центра сферы). Это недостаток в равной мере свойственен всем линейным алгоритмам и может быть преодолен за счет использования дополнительных фиктивных переменных, являющихся нелинейными функциями от элементов набора входных данных (т.н. kernel trick).
Второй недостаток метода главных компонент состоит в том, что направления, максимизирующие дисперсию, далеко не всегда максимизируют информативность. Например, переменная с максимальной дисперсией может не нести почти никакой информации, в то время как переменная с минимальной дисперсией позволяет полностью разделить классы. Метод главных компонент в данном случае отдаст предпочтение первой (менее информативной) переменной. Вся дополнительная информация, связанная с вектором (например, принадлежность образа к одному из классов), игнорируется.
Слайд 14
Пример данных для МГК
К. Эсбенсен. Анализ многомерных данных, сокр.
пер. с англ. под ред. О. Родионовой, Из-во ИПХФ
РАН, 2005
Слайд 18
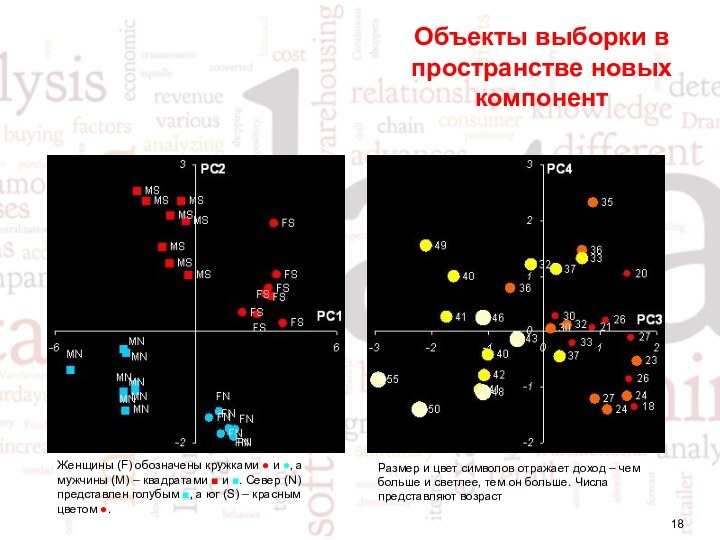
Объекты выборки в пространстве новых компонент
Женщины (F) обозначены
кружками ● и ●, а мужчины (M) – квадратами ■ и ■. Север (N) представлен голубым ■,
а юг (S) – красным цветом ●.Размер и цвет символов отражает доход – чем больше и светлее, тем он больше. Числа представляют возраст
Слайд 21
Метод главных факторов
В парадигме метода главных факторов задача
снижения размерности признакового пространства выглядит так, что n признаков
можно объяснить с помощью меньшего количества m-латентных признаков - общих факторов, где m<Каждый признак является результатом воздействия m гипотетических общих и одного характерного факторов:
Слайд 22
Вращение факторов
Вращение - это способ превращения факторов, полученных
на предыдущем этапе, в более осмысленные. Вращение делится на:
графическое (проведение осей, не применяется при более чем двухмерном анализе), аналитическое (выбирается некий критерий вращения, различают ортогональное и косоугольное) и
матрично-приближенное (вращение состоит в приближении к некой заданной целевой матрице).
Результатом вращения является вторичная структура факторов. Первичная факторная структура (состоящая из первичных нагрузок (полученных на предыдущем этапе) - это, фактически, проекции точек на ортогональные оси координат. Очевидно, что если проекции будут нулевыми, то структура будет проще. А проекции будут нулевыми, если точка лежит на какой-то оси. Таким образом, можно считать вращение переходом от одной системы координат к другой при известных координатах в одной системе( первичные факторы) и итеративно подбираемых координатах в другой системе (вторичные факторы). При получении вторичной структуры стремятся перейти к такой системе координат, чтобы провести через точки (объекты) как можно больше осей, чтобы как можно больше проекции (и соответственно нагрузок) были нулевыми. При этом могут сниматься ограничения ортогональности и убывания значимости от первого к последнему факторам, характерные для первичной структуры.
Слайд 23
Ортогональное вращение
Ортогональное вращение подразумевает, что мы будем вращать
факторы, но не будем нарушать их ортогональности друг другу.
Ортогональное вращение подразумевает умножение исходной матрицы первичных нагрузок на ортогональную матрицу R(такую матрицу, что )V=BR
Алгоритм ортогонального вращения в общем случае таков:
0. B - матрица первичных факторов.
Ищем ортогональную матрицу RT размера 2*2 для двух столбцов(факторов) bi и bj матрицы B такую, что критерий для матрицы [bibj] R максимален.
Заменяем столбцы bi и bj на столбцы .
Проверяем, все ли столбцы перебрали. Если нет, то переход на 1.
Проверяем, что критерий для всей матрицы вырос. Если да, то переход на 1. Если нет, то конец алгоритма.
Слайд 24
Варимаксное вращение
Этот критерий использует формализацию сложности фактора через
дисперсию квадратов нагрузок переменной:
Тогда критерий в общем виде можно
записать как:При этом, факторные нагрузки могут нормироваться для избавления от влияния отдельных переменных.
Слайд 25
Квартимаксное вращение
Формализуем понятие факторной сложности q i-ой переменной
через дисперсию квадратов факторных нагрузок факторов:
где r - число
столбцов факторной матрицы, bij - факторная нагрузка j-го фактора на i-ю переменную, - среднее значение. Критерий квартимакс старается максимизировать сложность всей совокупности переменных, чтобы достичь легкости интерпретации факторов (стремится облегчить описание столбцов):Учитывая, что - константа (сумма собственных чисел матрицы ковариации) и раскрыв среднее значение (а также учтя, что степенная функция растет пропорционально аргументу), получим окончательный вид критерия для максимизации:
Слайд 26
Критерии определения числа факторов
Главной проблемой факторного анализа является
выделение и интерпретация главных факторов. При отборе компонент исследователь
обычно сталкивается с существенными трудностями, так как не существует однозначного критерия выделения факторов, и потому здесь неизбежен субъективизм интерпретаций результатов. Существует несколько часто употребляемых критериев определения числа факторов. Некоторые из них являются альтернативными по отношению к другим, а часть этих критериев можно использовать вместе, чтобы один дополнял другой:Критерий Кайзера или критерий собственных чисел. Этот критерий предложен Кайзером, и является, вероятно, наиболее широко используемым. Отбираются только факторы с собственными значениями равными или большими 1. Это означает, что если фактор не выделяет дисперсию, эквивалентную, по крайней мере, дисперсии одной переменной, то он опускается.
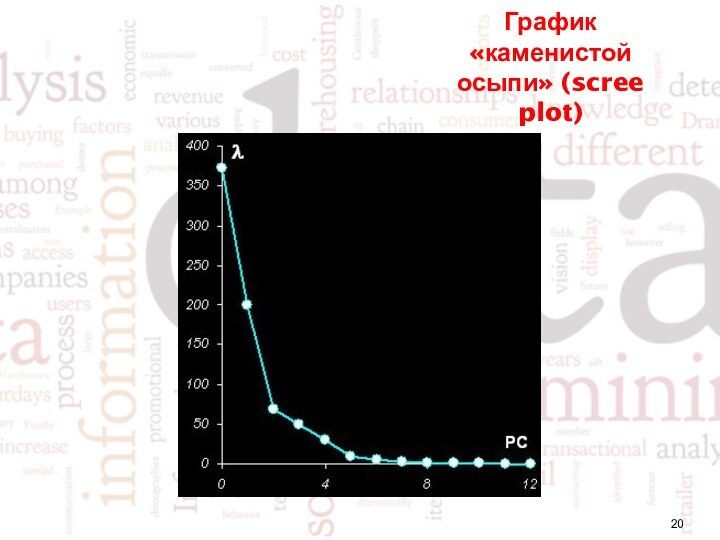
Критерий каменистой осыпи (англ. scree) или критерий отсеивания. Он является графическим методом, впервые предложенным психологом Кэттелом. Собственные значения возможно изобразить в виде простого графика. Кэттел предложил найти такое место на графике, где убывание собственных значений слева направо максимально замедляется. Предполагается, что справа от этой точки находится только «факториальная осыпь» — «осыпь» является геологическим термином, обозначающим обломки горных пород, скапливающиеся в нижней части скалистого склона.
Слайд 27
Критерии определения числа факторов. Продолжение
Критерий значимости. Он особенно
эффективен, когда модель генеральной совокупности известна и отсутствуют второстепенные
факторы. Но критерий непригоден для поиска изменений в модели и реализуем только в факторном анализе по методу наименьших квадратов или максимального правдоподобия.Критерий доли воспроизводимой дисперсии. Факторы ранжируются по доле детерминируемой дисперсии, когда процент дисперсии оказывается несущественным, выделение следует остановить. Желательно, чтобы выделенные факторы объясняли более 80 % разброса. Недостатки критерия: во-первых, субъективность выделения, во-вторых, специфика данных может быть такова, что все главные факторы не смогут совокупно объяснить желательного процента разброса. Поэтому главные факторы должны вместе объяснять не меньше 50,1 % дисперсии.
Критерий интерпретируемости и инвариантности. Данный критерий сочетает статистическую точность с субъективными интересами. Согласно ему, главные факторы можно выделять до тех пор, пока будет возможна их ясная интерпретация. Она, в свою очередь, зависит от величины факторных нагрузок, то есть если в факторе есть хотя бы одна сильная нагрузка, он может быть интерпретирован. Возможен и обратный вариант — если сильные нагрузки имеются, однако интерпретация затруднительна, от этой компоненты предпочтительно отказаться.
Слайд 28
Пример использования МГК
Пусть имеются следующие показатели экономической деятельности
предприятия: трудоемкость (x1), удельный вес покупных изделий в продукции (x2), коэффициент
сменности оборудования (x3), удельный вес рабочих в составе предприятия (x4), премии и вознаграждения на одного работника (x5), рентабельность (y). Линейная регрессионная модель имеет вид:y = b0 + b1*x1 + b2*x2 + b3*x3 + b4*x4 + b5*x5
Слайд 29
Пример использования МГК
Построение регрессионной модели в статистическом пакете
показывает, что коэффициент X4 не значим (p-Value > α
= 5%) , и его можно исключить из модели.После исключения X4 снова запускается процесс построения модели.
Слайд 30
Пример использования МГК
Критерий Кайзера для МГК показывает, что
можно оставить 2 компоненты, объясняющие около 80% исходной дисперсии.
Для
выделенных компонент можно построить уравнения в исходной системе координат:U1 = 0,41*x1 - 0,57*x2 + 0,49*x3 - 0,52*x5 U2 = 0,61*x1 + 0,38*x2 - 0,53*x3 - 0,44*x5
Слайд 31
Пример использования МГК
Теперь можно построить в новых компонентах
новую регрессионную модель:
y = 15,92 - 3,74*U1 - 3,87*U2
Слайд 32
Метод сингулярного разложения (SVD)
Beltrami и Jordan считаются основателями
теории сингулярного разложения. Beltrami – за то, что он
первым опубликовал работу о сингулярном разложении, а Jordan – за элегантность и полноту своей работы. Работа Beltrami появилась в журнале “Journal of Mathematics for the Use of the Students of the Italian Universities” в 1873 году, основная цель которой заключалась в том, чтобы ознакомить студентов с билинейными формами.Суть метода в разложении матрицы A размера n x m с рангом d = rank (M) <= min(n,m) в произведение матриц меньшего ранга:A =UDVT,
где матрицы U размера n x d и V размера m x d состоят из ортонормальных столбцов, являющихся собственными векторами при ненулевых собственных значениях матриц AAT и ATA соответственно и UTU = V TV = I , а D размера d x d - диагональная матрица с положительными диагональными элементами, отсортированными в порядке убывания. Столбцы матрицы U представляют собой, ортонормальный базис пространства столбцов матрицы A, а столбцы матрицы V – ортонормальный базис пространства строк матрицы A.