Презентация на тему Поиск простых чисел. PascalABC, FreePascal

простым, если оно делится только на себя и на

1.

Простые числа:

2, 3, 5, 7, 11, 13, 17, 19, 23,
29, 31, 37, 41, 43, 47, …

являющееся простым, называется составным

Составные числа:

4, 6, 8, 9, 10,

12, 14, 15, 16, 18,
20, 21, 22, 24, 25, 26, 27, 28, 30, 32,
33, 34, 35, 36, 38, 39, 40, 42, 44, 45,
46, 48, 49, 50, …

к простым, ни к составным.
Среди простых чисел только одно

чётное число 2. Остальные числа нечетные.
Простых чисел бесконечно много.

Существует множество задач, связанных с простыми числами, и хотя формулируются они достаточно просто, решить их бывает очень трудно. Некоторые свойства простых чисел еще не открыты. Немецкий математик Германа Вейль (Wayl, 1885-1955) так охарактеризовал простые числа: «Простые числа – это такие существа, которые всегда склонны прятаться от исследователя».
Во все времена люди хотели найти как можно большее простое число. Пока люди считали только при помощи карандаша и бумаги, им нечасто удавалось обнаружить новые простые числа. До 1952 г. самое большое известное простое число состояло из 39 цифр. Теперь поиском все больших простых чисел занимаются компьютеры. Но для них нужно составлять программы.

647).
Определить, является ли оно простым или составным.


Решение:
Будем делить

данное число N на все отличные от 1 числа, меньшие N. Если N не разделится ни на одно из этих чисел, то оно будет простым.
Например, введенное число 37. Следовательно, мы делим это число на числа 2, 3, 4, 5, 6, 7, 8, …, 34, 35, 36.

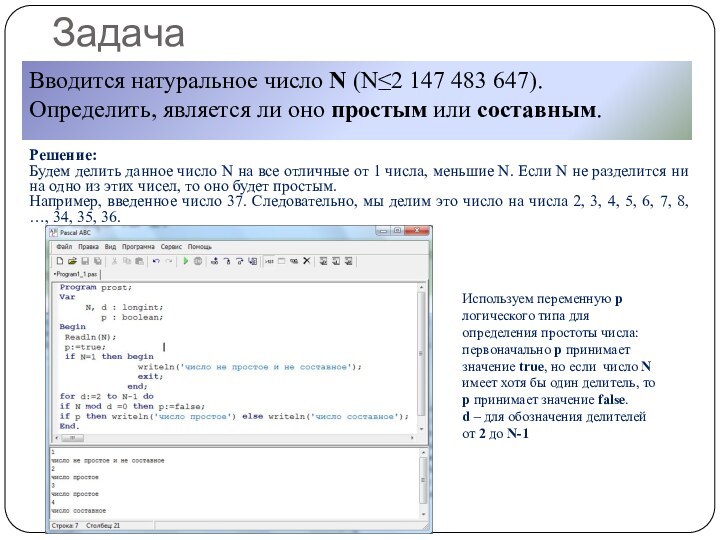
Используем переменную p логического типа для определения простоты числа: первоначально p принимает значение true, но если число N имеет хотя бы один делитель, то p принимает значение false.
d – для обозначения делителей от 2 до N-1

647). Определить, является ли оно простым или составным.
Выполним эту

программу, при

N=123 Ответ: число составное
N=131071 Ответ: число простое
N=524387 Ответ: число простое
N= 536870911 Ответ: число составное
N= 1999999991 Ответ: ?
N= 2147483647 Ответ: ?

Вы дождались ответа?

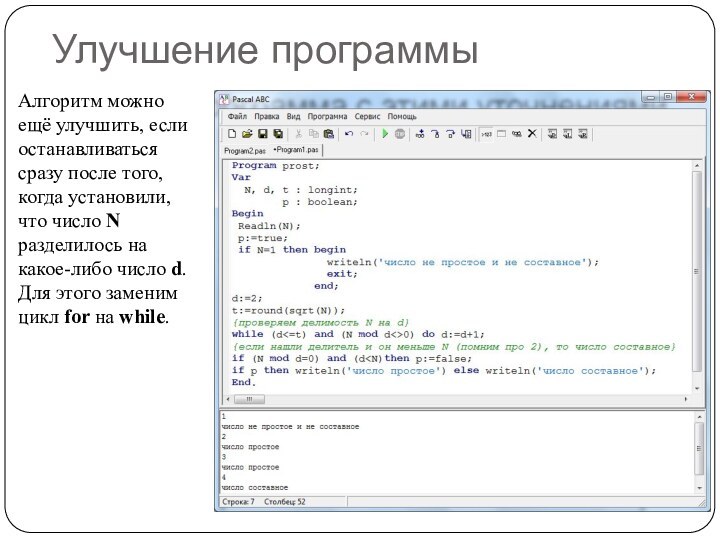
Для уменьшения времени работы программы нужно что-то придумать !

Вы дождётесь ответа?

на числа от 2 до N-1, т.е. мы искали

делители числа N, не равные 1 и меньшие N. На самом же деле можно число N проверять на делимость не всех чисел, а только от 2 до N/2. Почему?


команду for d:=2 to N-1 do …

заменим на for d:=2 to N div 2 do …

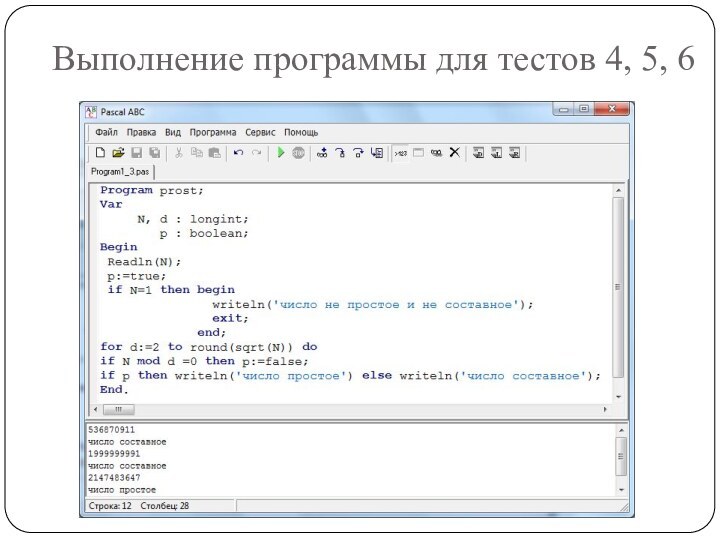
Таким образом, мы увеличили скорость выполнения программы в 2 раза, но тесты 4 - 6 всё равно выполняются долго.

представить в виде N=x∙y, где x и y больше

1, а меньшее из них обязательно не больше . Понятно, что если N делится на x, то N делится и на y. Если N не делится ни на одно число от 2 до round(sqrt(N)), значит оно не делится ни на какое другое число, т.е. оно простое.

команду for d:=2 to N div 2 do …
заменим на for d:=2 to round(sqrt(N)) do …

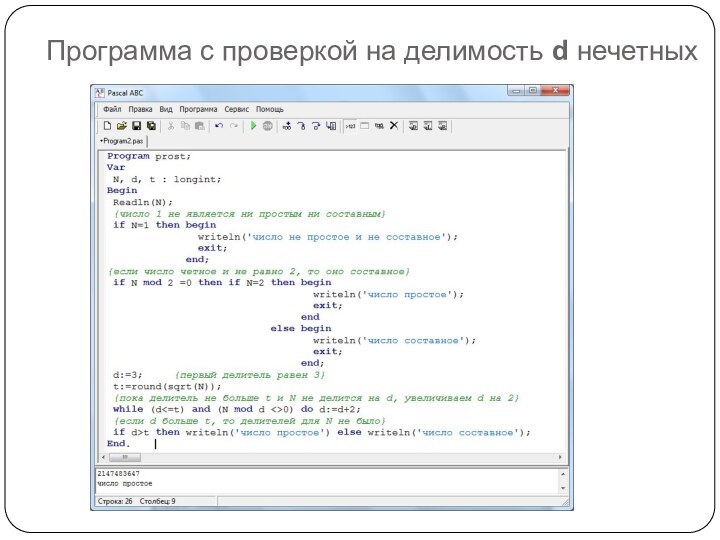
Что ещё можно заметить?

после того, когда установили, что число N разделилось на

какое-либо число d.
Для этого заменим цикл for на while.

уменьшили количество проверок делимости сначала в 2 раза, а

затем приблизительно в раз.

Можно ли ещё улучшить алгоритм?

Ещё в самом начале было замечено, что «среди простых чисел только одно чётное число 2. Остальные числа нечетные». Ясно также, что достаточно проверить делимость только на нечетные d.

простых чисел четные?
Назовите самое маленькое простое число?
Сколько однозначных простых

чисел?
К каким числам относится число 1?
Число 29 является простым? Какое самое близкое к нему будет простым?
Число 49 является простым? Какое самое близкое к нему будет простым?
Запишите в тетрадь следующие числа:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
38 39 40 41 42 43 44 45 46 47 48 49 50
Зачеркните все составные числа.
Какой алгоритм Вы будете использовать для определения является ли введенное натуральное число простым или составным? Опишите его.