Презентация на тему Получение схемы логического элемента

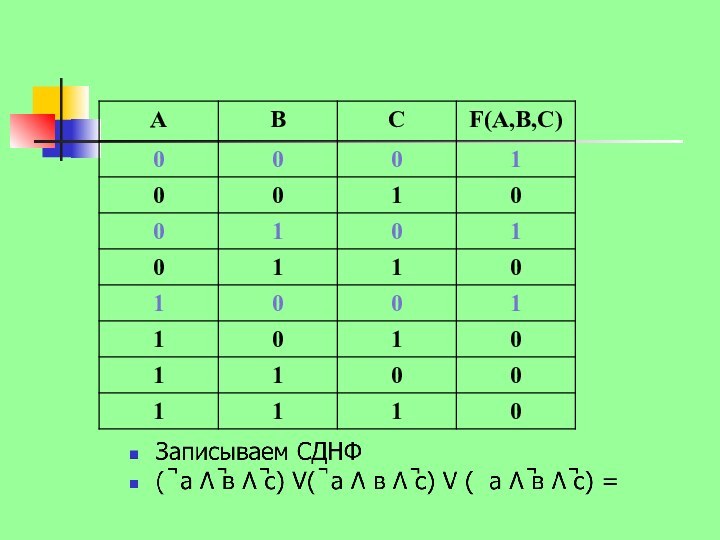
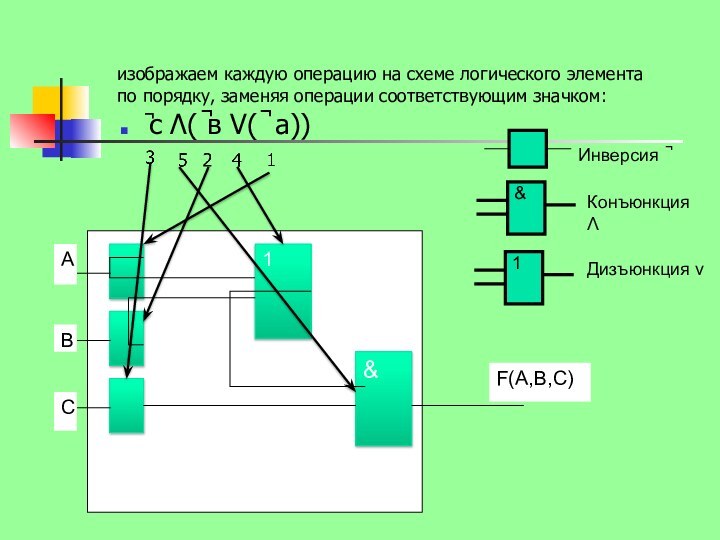
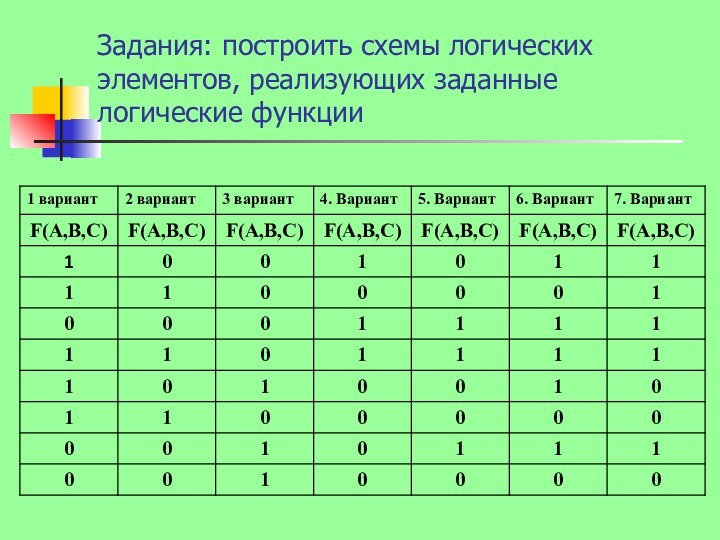
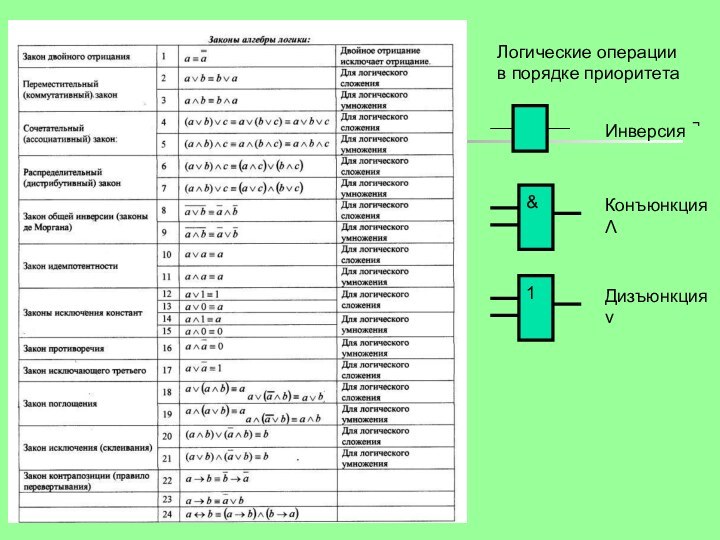
конъюнкция нескольких переменных, взятых с отрицанием или без отрицания,

причем среди переменных могут быть одинаковые: ¬C Λ C; C Λ ¬A; ¬C Λ B Λ ¬A ;
Дизъюнкция –логическое сложение.
Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые: ¬CVC; CV¬A; ¬CVBV¬A ;

нормальной формой (ДНФ): (CΛCΛ¬B)V(¬CΛA)
Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной 

нормальной формой (КНФ): (CVCV¬ B)Λ(¬CVA)

нет одинаковых элементарных конъюнкций и все конъюнкции состоят из

одного и того же набора переменных, в который каждая переменная входит только один раз ( возможно с отрицанием) (C Λ B Λ ¬A)V (C Λ B Λ A)
 Cовершенной КНФ называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз  ( возможно с отрицанием) (¬ CVBVA) Λ(C V¬BVA)

значений логической функции
Записываем исходные значения логических переменных.
Применяем СДНФ (так

как значений «1» меньше):
Обрабатываем те строки ТИ, в последнем столбце которых стоят «1»
Выписываем для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение логической переменной в данной строке =1, то в конъюнкцию включают саму эту переменную, если =0, то ее отрицание:
Все полученные конъюнкции связать в дизъюнкцией (записать произведение сумм):
Упрощаем логическое выражение, применяя законы алгебры логики
Склеивания
Распределительный
Поглощения

выражениям ( ̚ а Λ ̚в Λ ̚с) V(

̚ а Λ в Λ ̚с) V( а Λ ̚в Λ ̚с) =
2) Применяем распределительный закон ( ̚в Λ ̚с) V( ̚ а Λ в Λ ̚с) =
3) Применяем закон поглощения ̚с Λ ( ̚в V( ̚ а Λ в))= ̚с Λ( ̚в V( ̚ а))
4) Проставляем на полученной формуле порядок выполнения логических операций согласно приоритета.

̚с Λ( ̚в V( ̚ а))

1

2

3

4

5

порядку, заменяя операции соответствующим значком:
Инверсия ̚
Конъюнкция Λ

Дизъюнкция v

̚с Λ( ̚в V( ̚ а))

среди значений функции значений «0»меньше, применяют СКНФ)

Отметить те строки

таблицы истинности, в последнем столбце которых стоят 0:
Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке =0, то в дизъюнкцию включают саму эту переменную, если =1, то ее отрицание:
Все полученные дизъюнкции связать в конъюнкцию(записать сумму произведений):
Упростить логическое выражение, применив законы
Склеивания
Распределительный
Поглощения
(Предлагается выполнить самостоятельно)

функции

в порядке приоритета

логического элемента с тремя логическими входами (X,Y,Z), содержащую не

менее семи логических операций.
Построить таблицу истинности к ней. Применить СКНФ или СДНФ.
Упростить по приведенному в презентации алгоритму.
Построить новую схему.