Слайд 2
Темы лекций
Поиск с возвращением. Задача о ферзях. Оценка
методом Монте-Карло.
Метод ветвей и границ. Общая схема. Задача
коммивояжёра (ЗК).
Метод ветвей и границ. ЗК (продолжение). Приближённые решения.
Динамическое программирование. Идея и общая схема. Оптимальное умножение матриц.
Динамическое программирование. Оптимальные БДП. Хорошие БДП. Аналогии.
02.02.2016
Поиск с возвращением
Слайд 3
Продолжение
Графы и структуры данных. Задачи связности.
Остовные деревья графа.
Алгоритм Краскала. Алгоритм ЯПД.
Непересекающиеся подмножества.
Обходы графа. Алгоритм Борувки для
МОД.
МОД как приближение в ЗК. Двусвязные компоненты (применение обхода в глубину).
ПВГ в орграфах. Топологическая сортировка. Сильно связные компоненты.
Кратчайшие пути в графе (1).
Кратчайшие пути в графе (2).
02.02.2016
Поиск с возвращением
Слайд 4
Лабораторные работы и курсовая работа
Задание 1.
Алгоритмы сортировки,
частичного упорядочения, хеширования.
Задание 2.
Перебор с возвращением (Backtracking).
Задание
3.
Метод ветвей и границ
Задание 4.
Динамическое программирование.
Курсовая работа (КР): Алгоритмы на графах.
02.02.2016
Поиск с возвращением
Слайд 5
02.02.2016
Поиск с возвращением
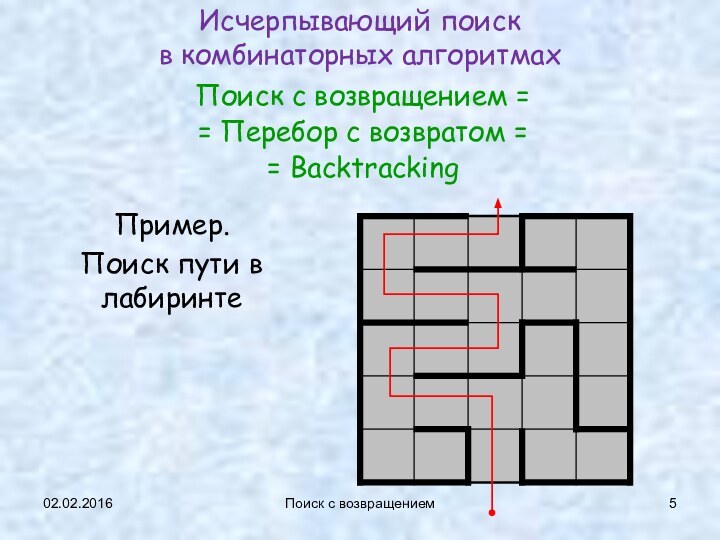
Исчерпывающий поиск
в комбинаторных алгоритмах
Поиск с возвращением
=
= Перебор с возвратом =
= Backtracking
Пример.
Поиск пути
в лабиринте
Слайд 6
02.02.2016
Поиск с возвращением
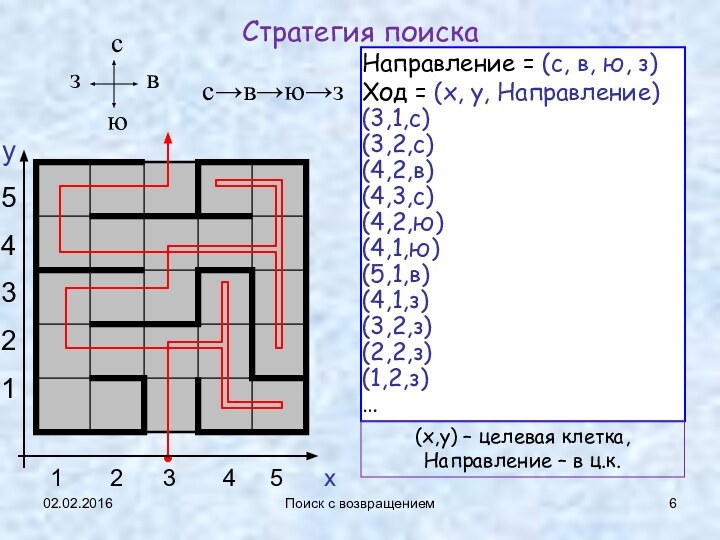
Стратегия поиска
с
в
ю
з
с→в→ю→з
Направление = (с, в, ю,
з)
Ход = (x, y, Направление)
(3,1,с)
(3,2,с)
(4,2,в)
(4,3,с)
(4,2,ю)
(4,1,ю)
(5,1,в)
(4,1,з)
(3,2,з)
(2,2,з)
(1,2,з)
…
1
2 3 4 5 x
y
5
4
3
2
1
(x,y) – целевая клетка,
Направление – в ц.к.
Слайд 7
02.02.2016
Поиск с возвращением
Общий алгоритм
Решение вида (a1, a2, a3,
…, an)
n – конечно, но, вообще говоря, заранее не
известно
ai∈ Ai ;
Ai – конечное линейно упорядоченное множество
Исчерпываем все элементы множества A1×A2×A3×…×Ai
i = 0 → ()
i = 1; S1 ⊂ A1; a1 ∈ S1; () → (a1)
i = 2; S2 ⊂ A2; a2 ∈ S2; (a1) → (a1, a2)
…
i = k; Sk ⊂ Ak; ak ∈ Sk; (a1,…, ak-1) → (a1,…, ak-1,ak)
При Sk = ∅ backtrack и новый выбор ak-1 ∈ Sk-1;
Слайд 8
02.02.2016
Поиск с возвращением
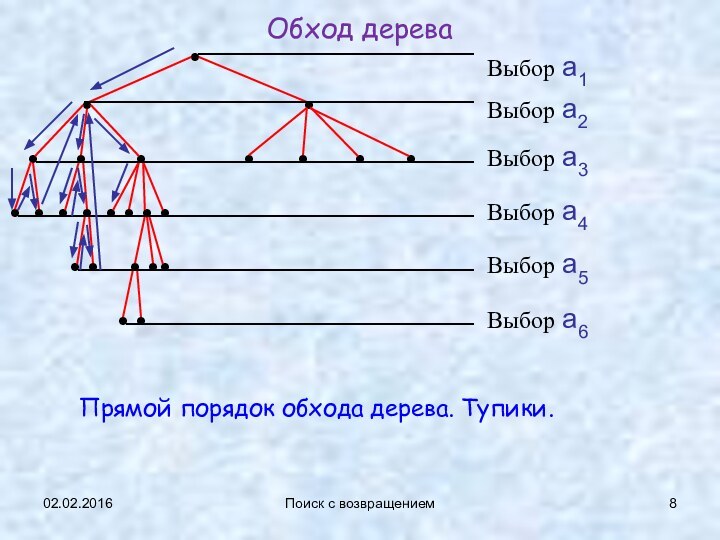
Обход дерева
Прямой порядок обхода дерева. Тупики.
Выбор
a1
Выбор a2
Выбор a3
Выбор a4
Выбор a5
Выбор a6
Слайд 9
02.02.2016
Поиск с возвращением
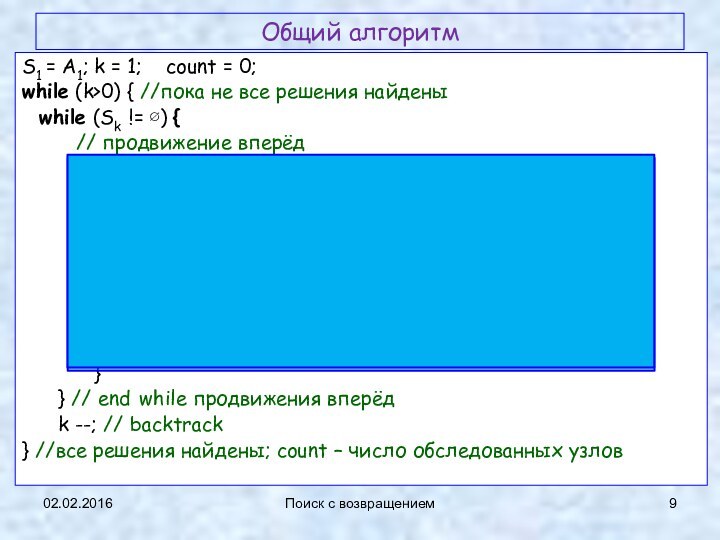
Общий алгоритм
S1 = А1; k = 1;
count = 0;
while (k>0) { //пока не все
решения найдены
while (Sk != ∅) {
// продвижение вперёд
ak = элемент из Sk; //выбор очередного элемента из Sk
Sk = Sk − {ak};
count ++;
if ((a1,…, ak-1,ak) – решение) { /*фиксировать решение*/}
else {
// переход к следующему уровню
k ++;
вычислить Sk;
}
} // end while продвижения вперёд
k --; // backtrack
} //все решения найдены; count – число обследованных узлов
Слайд 10
Пример задачи,
решаемой алгоритмом по этой схеме
02.02.2016
Поиск с
возвращением
Слайд 11
02.02.2016
Поиск с возвращением
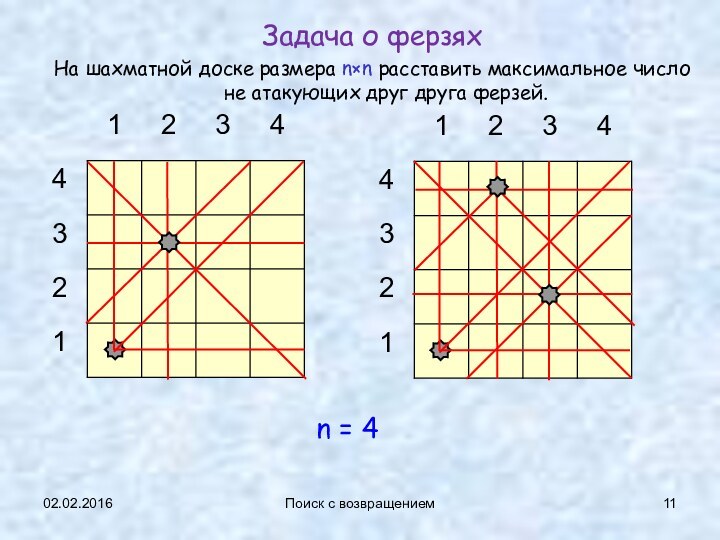
Задача о ферзях
На шахматной доске размера
n×n расставить максимальное число не атакующих друг друга ферзей.
n
= 4
Слайд 12
02.02.2016
Поиск с возвращением
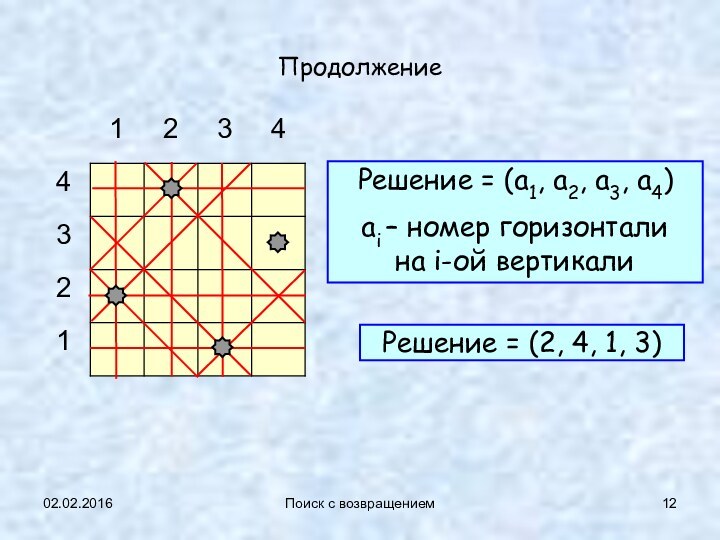
Продолжение
Решение = (2, 4, 1, 3)
Решение
= (a1, a2, a3, a4)
ai – номер горизонтали
на i-ой вертикали
Слайд 13
02.02.2016
Поиск с возвращением
Решение (a1, a2, …, an)
Ферзи i
и k атакуют друг друга:
i = k - ферзи
на одной вертикали
ai = ak - ферзи на одной горизонтали
⏐ai - ak⏐ = ⏐i - k⏐ - ферзи на одной диагонали
Наращивание (продолжение) решения
(a1, a2, …, ak-1)∙ak = (a1, a2, …, ak-1, ak )
Слайд 14
02.02.2016
Поиск с возвращением
Ak = (1, 2, …,n) –
номера клеток вертикалей.
Множество Sk явно не формируется,
но, выбирая
очередного кандидата αk ∈ Ak, проверяем α k ∈ Sk
Используется sk - нижняя граница в Ak,
т.о. кандидаты в Sk выбираются из множества
(sk, sk+1, …, n) , т.е. Sk ⊂ (sk, sk+1, …, n).
Обсудить альтернативу.
Слайд 15
02.02.2016
Поиск с возвращением
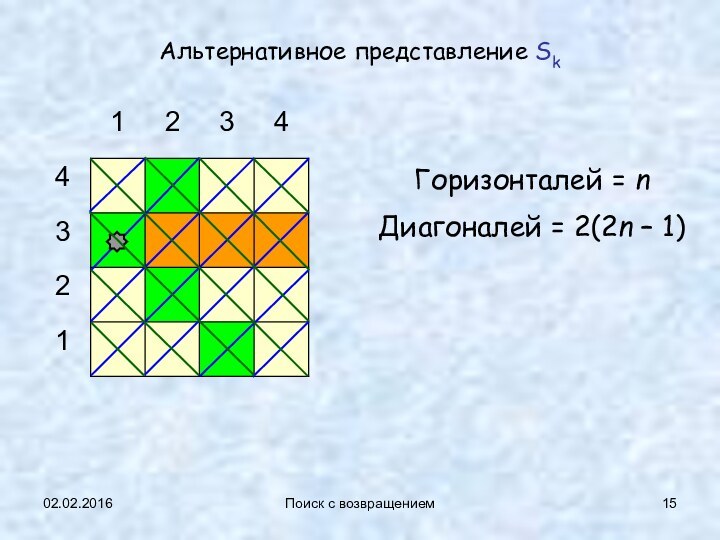
Альтернативное представление Sk
Горизонталей = n
Диагоналей =
2(2n – 1)
Слайд 16
02.02.2016
Поиск с возвращением
Проверка s[k]
bool noQueen (uns s,
uns k)
// ферзь не может быть поставлен в
строку s столбца k
{ bool Flag = true;
uns i = 1;
while ((i // Flag='ферзи [1..i) не атакуют поле '
// атакует ли ферзь из i-го столбца поле ?}
Flag = !( (a[i]==s) || (abs(a[i]-s)== k-i) );
i++;
} //end - while
return (!Flag);
} // end noQueen
Слайд 17
02.02.2016
Поиск с возвращением
Нахождение очередного свободного поля s[k]
/*найти следующее
наименьшее значение s[k],
начиная с текущего s[k];
если такового нет, то s[k]=n+1
*/
while ((s[k]<=n) && noQueen (s[k],k)) s[k]++;
Слайд 18
02.02.2016
Поиск с возвращением
Реализация
void queen1(const uns n)
{ pos s;
/*s[k]
- наименьший элемент множества Sk неопробованных (допустимых) значений
*/
uns count
= 0; // счётчик обследованных // узлов дерева поиска
uns countS = 0; // счётчик найденых решений
a[1] = 1; s[1] = 1;
uns k = 1;
Слайд 19
02.02.2016
Поиск с возвращением
while (k>0) {
while ((k>=1) && (s[k]
{
a[k]= s[k]; s[k]++;
// найти следующее наименьшее значение s[k]
while ((s[k]
&& noQueen (s[k],k)) s[k]++;
count++;
if (k==n) {countS++; …} //решение найдено - фиксировать !
else {// переход к следующей вертикали
k++;
s[k]= 1;
//найти следующее наименьшее значение s[k],
while ((s[k]<=n) && noQueen (s[k],k)) s[k]++;
}
}
k--; // backtrack
}
Слайд 20
Демонстрация
02.02.2016
Поиск с возвращением
Слайд 21
02.02.2016
Поиск с возвращением
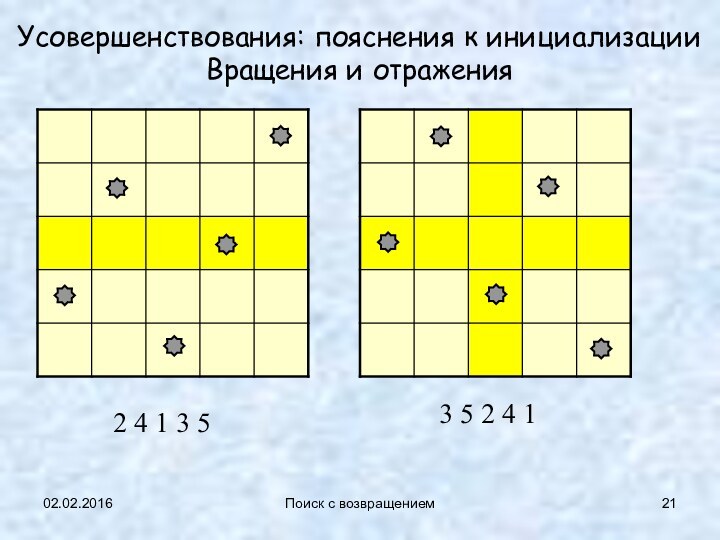
Усовершенствования: пояснения к инициализации
Вращения и отражения
2
4 1 3 5
3 5 2 4 1
Слайд 22
02.02.2016
Поиск с возвращением
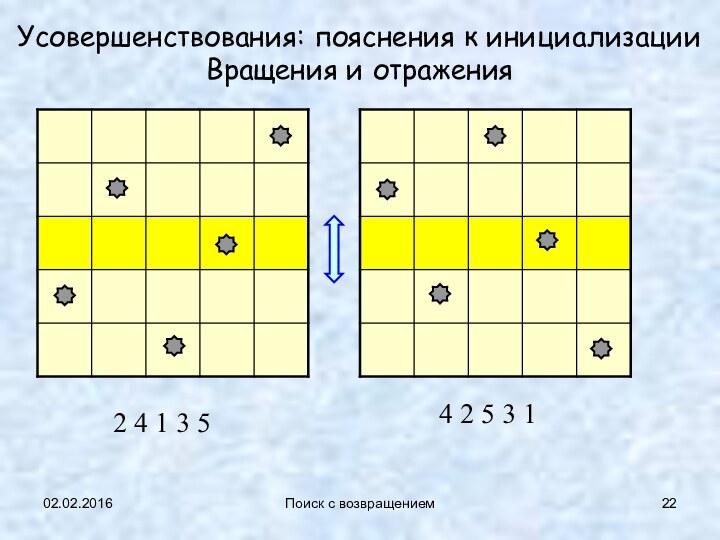
Усовершенствования: пояснения к инициализации
Вращения и отражения
2
4 1 3 5
4 2 5 3 1
Слайд 23
02.02.2016
Поиск с возвращением
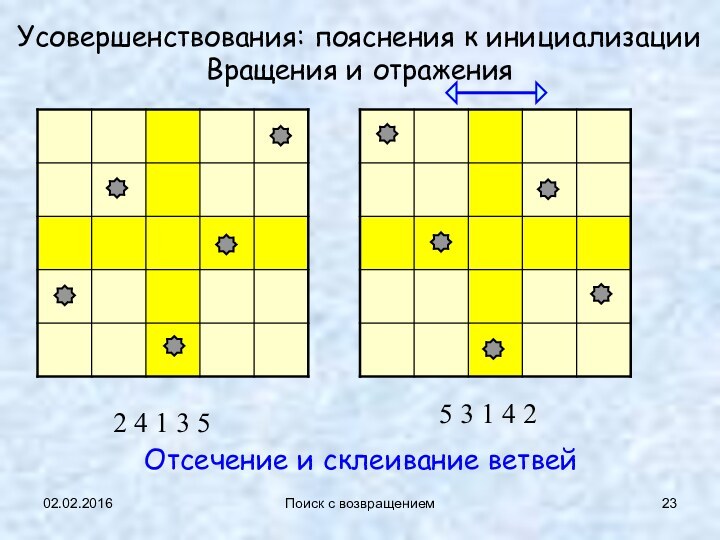
Усовершенствования: пояснения к инициализации
Вращения и отражения
2
4 1 3 5
5 3 1 4 2
Отсечение и
склеивание ветвей
Слайд 24
Усовершенствования
02.02.2016
Поиск с возвращением
void queen1(const uns n)
{pos s; //s[k]
- наименьший элемент множества Sk //неопробованных (допустимых) значений
uns count
= 1; // счётчик обследованных узлов
uns countS = 0; // счётчик найденных решений
uns n_div_2 = n/2;
a[1] = 2; s[1] = 3;
uns k = 2; s[2] = 4;
while (k>0){
while ( ((k>1) && (s[k]<=n)) || ((k==1) && (s[1]<=(n_div_2))) )
{ a[k]= s[k];
…
}
Слайд 25
02.02.2016
Поиск с возвращением
Подсчет вариантов
n=8
Все возможные способы C(n2|n) ≈
4,4*109
В каждом столбце один nn ≈ 1,7*107
+
В каждой строке один n! ≈ 4,0*104
На каждой диагонали не более одного 2056
Усовершенствования (вращения и отражения) 801
Слайд 26
02.02.2016
Поиск с возвращением
Результаты
количество ферзей = 4
р е ш
е н и я :
1 :: 2
4 1 3
всего вершин = 4
количество ферзей = 5
р е ш е н и я :
1 :: 2 4 1 3 5
2 :: 2 5 3 1 4
всего вершин = 11
количество ферзей = 6
р е ш е н и я :
1 :: 2 4 6 1 3 5
2 :: 3 6 2 5 1 4
всего вершин = 54
количество ферзей = 7
р е ш е н и я :
1 :: 2 4 1 7 5 3 6
2 :: 2 4 6 1 3 5 7
3 :: 2 5 1 4 7 3 6
4 :: 2 5 3 1 7 4 6
5 :: 2 5 7 4 1 3 6
6 :: 2 6 3 7 4 1 5
7 :: 2 7 5 3 1 6 4
8 :: 3 1 6 2 5 7 4
9 :: 3 1 6 4 2 7 5
10 :: 3 5 7 2 4 6 1
11 :: 3 6 2 5 1 4 7
12 :: 3 7 2 4 6 1 5
13 :: 3 7 4 1 5 2 6
всего вершин = 164
Слайд 27
02.02.2016
Поиск с возвращением
количество ферзей = 8
р е ш
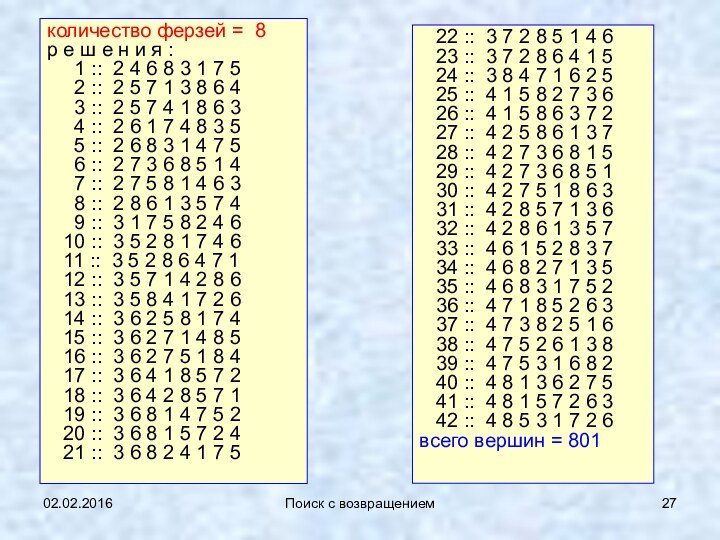
е н и я :
1 ::
2 4 6 8 3 1 7 5
2 :: 2 5 7 1 3 8 6 4
3 :: 2 5 7 4 1 8 6 3
4 :: 2 6 1 7 4 8 3 5
5 :: 2 6 8 3 1 4 7 5
6 :: 2 7 3 6 8 5 1 4
7 :: 2 7 5 8 1 4 6 3
8 :: 2 8 6 1 3 5 7 4
9 :: 3 1 7 5 8 2 4 6
10 :: 3 5 2 8 1 7 4 6
11 :: 3 5 2 8 6 4 7 1
12 :: 3 5 7 1 4 2 8 6
13 :: 3 5 8 4 1 7 2 6
14 :: 3 6 2 5 8 1 7 4
15 :: 3 6 2 7 1 4 8 5
16 :: 3 6 2 7 5 1 8 4
17 :: 3 6 4 1 8 5 7 2
18 :: 3 6 4 2 8 5 7 1
19 :: 3 6 8 1 4 7 5 2
20 :: 3 6 8 1 5 7 2 4
21 :: 3 6 8 2 4 1 7 5
22 :: 3 7 2 8 5 1 4 6
23 :: 3 7 2 8 6 4 1 5
24 :: 3 8 4 7 1 6 2 5
25 :: 4 1 5 8 2 7 3 6
26 :: 4 1 5 8 6 3 7 2
27 :: 4 2 5 8 6 1 3 7
28 :: 4 2 7 3 6 8 1 5
29 :: 4 2 7 3 6 8 5 1
30 :: 4 2 7 5 1 8 6 3
31 :: 4 2 8 5 7 1 3 6
32 :: 4 2 8 6 1 3 5 7
33 :: 4 6 1 5 2 8 3 7
34 :: 4 6 8 2 7 1 3 5
35 :: 4 6 8 3 1 7 5 2
36 :: 4 7 1 8 5 2 6 3
37 :: 4 7 3 8 2 5 1 6
38 :: 4 7 5 2 6 1 3 8
39 :: 4 7 5 3 1 6 8 2
40 :: 4 8 1 3 6 2 7 5
41 :: 4 8 1 5 7 2 6 3
42 :: 4 8 5 3 1 7 2 6
всего вершин = 801
Слайд 28
02.02.2016
Поиск с возвращением
количество ферзей = 9
р е ш

е н и я :
1 :: 2
4 1 7 9 6 3 5 8
2 :: 2 4 7 1 3 9 6 8 5
3 :: 2 4 8 3 9 6 1 5 7
4 :: 2 4 9 7 3 1 6 8 5
5 :: 2 4 9 7 5 3 1 6 8
6 :: 2 5 7 1 3 8 6 4 9
7 :: 2 5 7 4 1 3 9 6 8
8 :: 2 5 7 9 3 6 4 1 8
9 :: 2 5 7 9 4 8 1 3 6
10 :: 2 5 8 1 3 6 9 7 4
11 :: 2 5 8 1 9 6 3 7 4
12 :: 2 5 8 6 9 3 1 4 7
13 :: 2 5 8 6 9 3 1 7 4
14 :: 2 5 9 4 1 8 6 3 7
15 :: 2 6 1 3 7 9 4 8 5
16 :: 2 6 1 7 4 8 3 5 9
17 :: 2 6 1 7 5 3 9 4 8
18 :: 2 6 1 9 5 8 4 7 3
19 :: 2 6 3 1 8 4 9 7 5
20 :: 2 6 9 3 5 8 4 1 7
21 :: 2 7 5 1 9 4 6 8 3
22 :: 2 7 5 8 1 4 6 3 9
23 :: 2 7 9 6 3 1 4 8 5
24 :: 2 8 1 4 7 9 6 3 5
25 :: 2 8 5 3 9 6 4 1 7
26 :: 2 8 6 9 3 1 4 7 5
27 :: 2 9 5 3 8 4 7 1 6
28 :: 2 9 6 3 5 8 1 4 7
29 :: 2 9 6 3 7 4 1 8 5
30 :: 2 9 6 4 7 1 3 5 8
31 :: 3 1 4 7 9 2 5 8 6
32 :: 3 1 6 8 5 2 4 9 7
33 :: 3 1 7 2 8 6 4 9 5
34 :: 3 1 7 5 8 2 4 6 9
35 :: 3 1 8 4 9 7 5 2 6
36 :: 3 1 9 7 5 2 8 6 4
37 :: 3 5 2 8 1 4 7 9 6
38 :: 3 5 2 8 1 7 4 6 9
39 :: 3 5 7 1 4 2 8 6 9
40 :: 3 5 8 2 9 6 1 7 4
41 :: 3 5 8 2 9 7 1 4 6
42 :: 3 5 9 2 4 7 1 8 6
43 :: 3 5 9 4 1 7 2 6 8
44 :: 3 6 2 7 1 4 8 5 9
45 :: 3 6 2 9 5 1 8 4 7
46 :: 3 6 8 1 4 7 5 2 9
47 :: 3 6 8 1 5 9 2 4 7
48 :: 3 6 8 2 4 9 7 5 1
49 :: 3 6 8 5 1 9 7 2 4
50 :: 3 6 8 5 2 9 7 4 1
51 :: 3 6 9 1 8 4 2 7 5
52 :: 3 6 9 2 5 7 4 1 8
53 :: 3 6 9 2 8 1 4 7 5
54 :: 3 6 9 5 8 1 4 2 7
55 :: 3 6 9 7 1 4 2 5 8
56 :: 3 6 9 7 2 4 8 1 5
57 :: 3 6 9 7 4 1 8 2 5
58 :: 3 7 2 4 8 1 5 9 6
59 :: 3 7 2 8 5 9 1 6 4
60 :: 3 7 2 8 6 4 1 5 9
61 :: 3 7 4 2 9 5 1 8 6
62 :: 3 7 4 2 9 6 1 5 8
63 :: 3 7 4 8 5 9 1 6 2
64 :: 3 7 9 1 5 2 8 6 4
65 :: 3 7 9 4 2 5 8 6 1
66 :: 3 8 2 4 9 7 5 1 6
67 :: 3 8 4 7 9 2 5 1 6
…………
…
90 :: 4 2 9 5 1 8 6 3 7
91 :: 4 6 1 5 2 8 3 7 9
92 :: 4 6 1 9 5 8 2 7 3
93 :: 4 6 1 9 7 3 8 2 5
94 :: 4 6 3 9 2 5 8 1 7
95 :: 4 6 3 9 2 8 5 7 1
96 :: 4 6 3 9 7 1 8 2 5
97 :: 4 6 8 2 5 1 9 7 3
98 :: 4 6 8 2 5 7 9 1 3
99 :: 4 6 8 2 7 1 3 5 9
100 :: 4 6 8 3 1 7 5 2 9
101 :: 4 6 9 3 1 8 2 5 7
102 :: 4 7 1 3 9 6 8 5 2
103 :: 4 7 1 6 9 2 8 5 3
104 :: 4 7 1 8 5 2 9 3 6
105 :: 4 7 3 6 9 1 8 5 2
106 :: 4 7 3 8 2 5 9 6 1
107 :: 4 7 3 8 6 1 9 2 5
108 :: 4 7 3 8 6 2 9 5 1
109 :: 4 7 5 2 9 1 3 8 6
110 :: 4 7 5 2 9 1 6 8 3
111 :: 4 7 5 2 9 6 8 3 1
112 :: 4 7 9 2 5 8 1 3 6
113 :: 4 7 9 2 6 1 3 5 8
114 :: 4 7 9 6 3 1 8 5 2
115 :: 4 8 1 5 7 2 6 3 9
116 :: 4 8 5 3 1 6 2 9 7
117 :: 4 8 5 3 1 7 2 6 9
118 :: 4 9 3 6 2 7 5 1 8
119 :: 4 9 5 3 1 6 8 2 7
120 :: 4 9 5 3 1 7 2 8 6
121 :: 4 9 5 8 1 3 6 2 7
всего вершин = 2857
Слайд 29
02.02.2016
Поиск с возвращением
Оценка сложности выполнения
Метод Монте-Карло
Число исследуемых
узлов дерева
- мощность множества Ai
В лучшем случае
≈ Const
и тогда число узлов дерева ≈ Сn
Слайд 30
02.02.2016
Поиск с возвращением
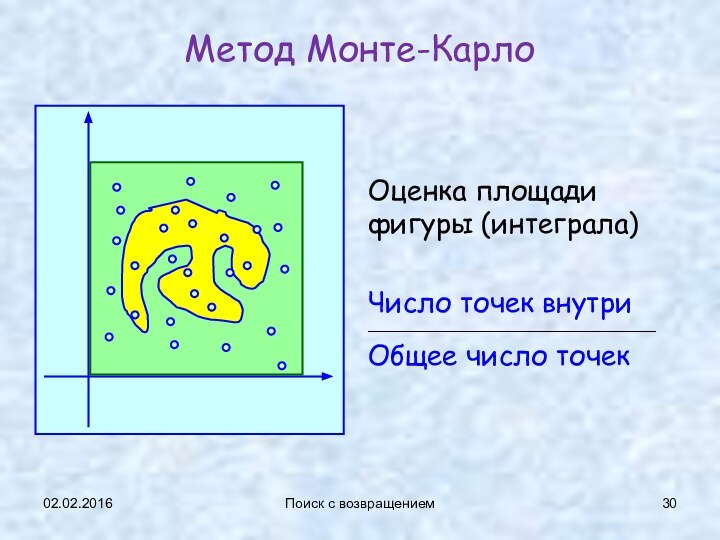
Метод Монте-Карло
Оценка площади фигуры (интеграла)
Число точек
внутри
______________________________________________
Общее число точек
Слайд 31
02.02.2016
Поиск с возвращением
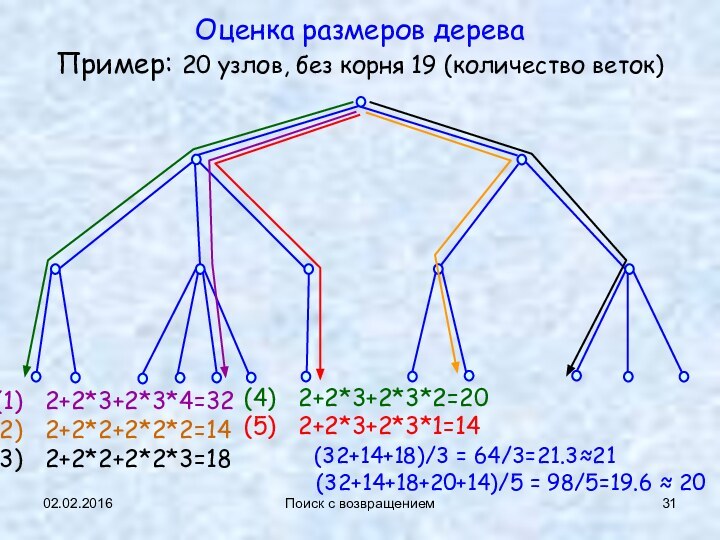
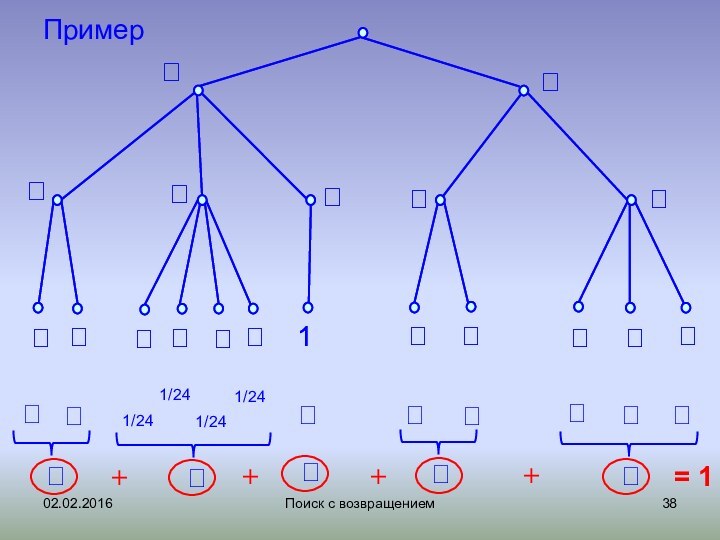
Оценка размеров дерева
Пример: 20 узлов, без
корня 19 (количество веток)
2+2*3+2*3*4=32
2+2*2+2*2*2=14
2+2*2+2*2*3=18
2+2*3+2*3*2=20
2+2*3+2*3*1=14
(32+14+18)/3 = 64/3=21.3≈21
(32+14+18+20+14)/5 = 98/5=19.6 ≈ 20
Слайд 32
02.02.2016
Поиск с возвращением
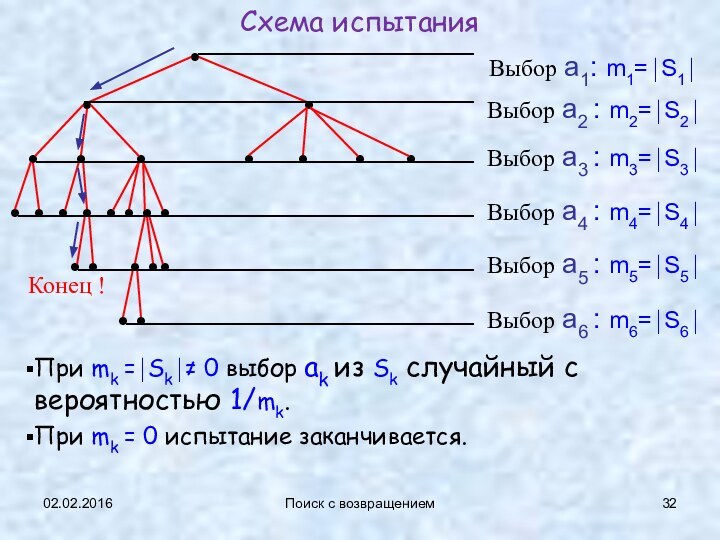
Схема испытания
При mk =⏐Sk⏐≠ 0 выбор
ak из Sk случайный с вероятностью 1/mk.
При mk =
0 испытание заканчивается.
Выбор a1: m1=⏐S1⏐
Выбор a2 : m2=⏐S2⏐
Выбор a3 : m3=⏐S3⏐
Выбор a4 : m4=⏐S4⏐
Выбор a5 : m5=⏐S5⏐
Выбор a6 : m6=⏐S6⏐
Конец !
Слайд 33
02.02.2016
Поиск с возвращением
Схема испытания
Случайная величина
V = m1 +
m1m2 + m1m2m3 + … + m1m2…mL
Математическое ожидание
E(V)
= число узлов в дереве (отличных от корня)
Напоминание: для случайной величины x с исходами x1, x2,…, xk и вероятностями p1, p2,…, pk
математическое ожидание есть
Слайд 34
Внимание!
На следующих слайдах 35-39 дано обоснование схемы Монте-Карло
(сл.40).
Это для студентов, которые хотят понять, почему эта схема
будет работать!
02.02.2016
Поиск с возвращением
Слайд 35
02.02.2016
Поиск с возвращением
Покажем, что
E(V) = число
узлов в дереве
1) функция на дереве T (не
случайная)
где ν - число братьев x, включая самого x
(т.е. число сыновей узла отец(x) )
Пусть путь от корня к узлу x есть v1, v2, …, vj , тогда
μ(x) = μ(vj) = νj× μ(vj-1) = νj × νj-1 × μ(vj-2) = … =
= νj × νj-1 × … × ν1 × μ(v1) = νj × νj-1 × … × ν1
Слайд 36
02.02.2016
Поиск с возвращением
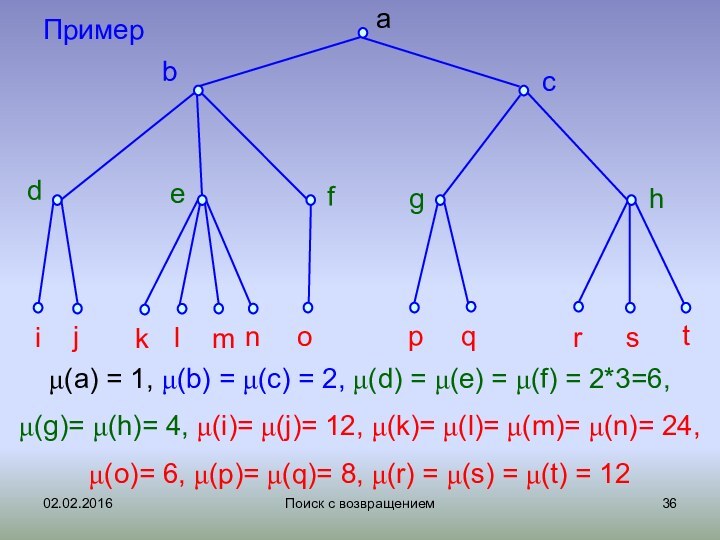
Пример
μ(a) = 1, μ(b) = μ(c)
= 2, μ(d) = μ(e) = μ(f) = 2*3=6,
μ(g)=
μ(h)= 4, μ(i)= μ(j)= 12, μ(k)= μ(l)= μ(m)= μ(n)= 24,
μ(o)= 6, μ(p)= μ(q)= 8, μ(r) = μ(s) = μ(t) = 12
Слайд 37
02.02.2016
Поиск с возвращением
2) Функция «индикатор», описывающая случайность
1, если
узел x пройден при испытании
I(x) =
0, если узел x
не пройден при испытании
Случайное событие = «узел x пройден»,
а I(x) − случайная величина ∈{0,1}
Вероятность дойти до узла x = vj есть
(1/m1) × (1/m2) × … × (1/mj)
Слайд 38
02.02.2016
Поиск с возвращением
Пример
1/24
1/24
1/24
1/24
+
+
+
+
= 1
Слайд 39
02.02.2016
Поиск с возвращением
Итак, покажем, что
E(V) =
число узлов в дереве
Слайд 40
02.02.2016
Поиск с возвращением
Общий алгоритм
// Монте-Карло
SV = 0; //
M – число испытаний
for (i = 1; i
{
k = 1; S1 = А1; m1 = ⏐S1⏐;
Sum = 0; Prod = 1;
while (mk ≠ 0) {
{ //продвижение вперёд
Prod* = mk;
Sum+ = Prod;
ak = случайный выбор очередного элемента из Sk;
k ++;
вычислить Sk и mk;
}
SV := SV + Sum; //добав. рез. очередного испытания
} // end - for
V = SV/ M;
Слайд 41
02.02.2016
Поиск с возвращением
begin { MonteCarlo }
Randomize; n_div_2
:= n div 2; all := 0;
for
iExp:=1 to nExp do
begin { очередное испытание }
m_k := n_div_2 - 1; num := Random ( m_k ) + 1;
a[1] := 1+num; k := 2; prod := m_k; sum := prod;
FormSk ( k, m_k, S_k );
while m_k<>0 do
begin
prod := prod*m_k; sum := sum + prod;
num := Random ( m_k ) + 1; a[k] := S_k[num];
k := k + 1; FormSk ( k, m_k, S_k );
end {while};
all := all + sum
end {for};
v := all/nExp
end { MonteCarlo };
Слайд 42
02.02.2016
Поиск с возвращением
procedure FormSk ( k: Nat;
var m_k: Nat0; var S_k: pos );
{ формирует
"множество" (вектор) S_k возможных ходов и
его мощность m_k; если S_k пусто, то m_k=0 }
var s: Nat;
begin
m_k := 0;
for s:=1 to n do
if not NoQueen( k, s) then
begin { можно ставить }
m_k := m_k + 1;
S_k[m_k] := s
end;
end {FormSk};
Слайд 43
02.02.2016
Поиск с возвращением
См. файлы с результатами
Queen
Queen_re
Слайд 44
02.02.2016
Поиск с возвращением
Backtracking.
Другие способы программирования
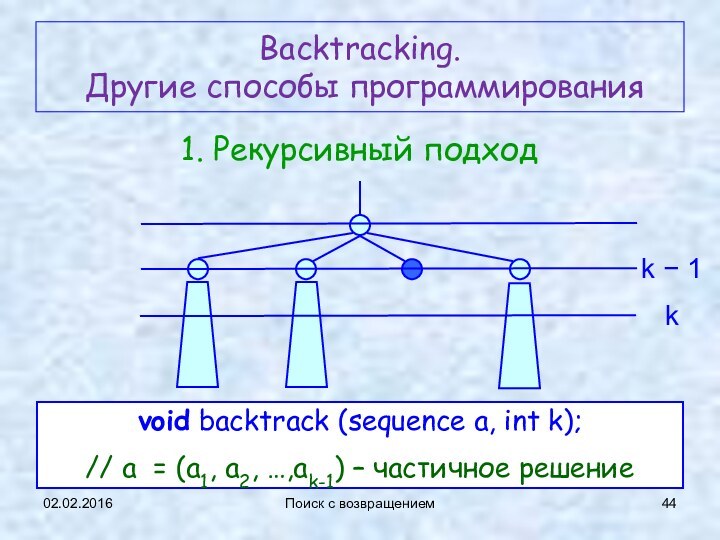
1. Рекурсивный подход
k
− 1
k
void backtrack (sequence a, int k);
// a =
(a1, a2, …,ak-1) – частичное решение
Слайд 45
02.02.2016
Поиск с возвращением
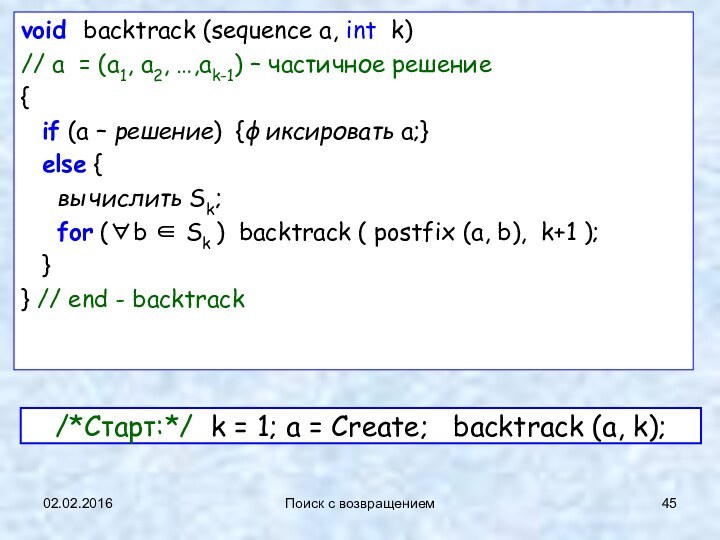
void backtrack (sequence a, int k)
//
a = (a1, a2, …,ak-1) – частичное решение
{
if
(a – решение) {фиксировать a;}
else {
вычислить Sk;
for (∀b ∈ Sk ) backtrack ( postfix (a, b), k+1 );
}
} // end - backtrack
/*Старт:*/ k = 1; a = Create; backtrack (a, k);
Слайд 46
02.02.2016
Поиск с возвращением
2. Макрокоманды
Уменьшение «накладных расходов»
(все решения одной
длины n)
Макрокоманда
CODEk: вычислить Sk;
Lk: if Sk = ∅ then
goto Lk-1;
ak = очередной элемент из Sk;
Sk := Sk − {ak};
Слайд 47
02.02.2016
Поиск с возвращением
Цикл периода макрогенерации:
for ( k =
1; k
…
CODEn;
фиксировать решение (a1, a2, …,an);
goto Ln;
L0: // конец – все решения найдены
Слайд 48
02.02.2016
Поиск с возвращением
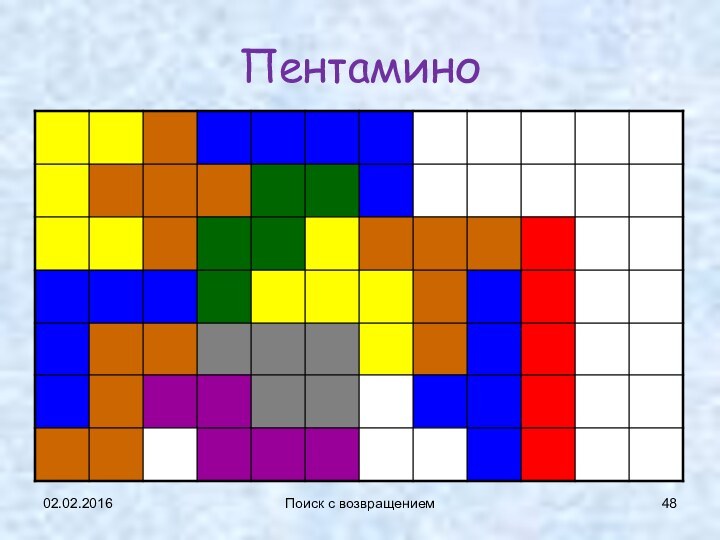
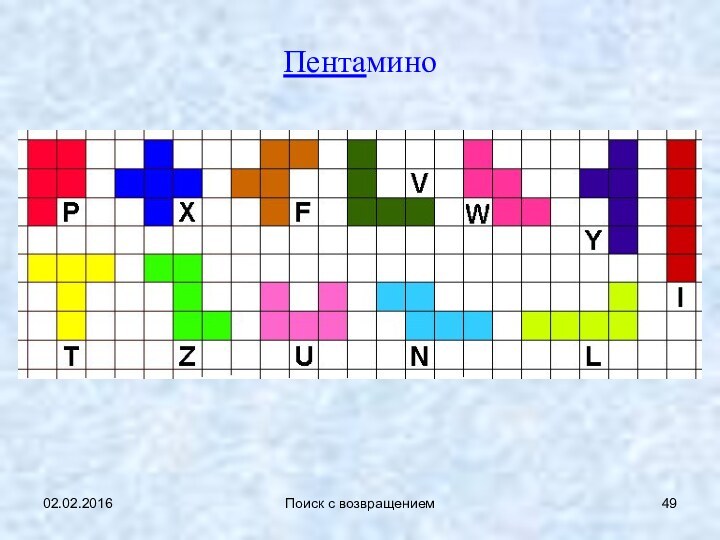
Пентамино
Слайд 49
02.02.2016
Поиск с возвращением
Пентамино
Слайд 51
02.02.2016
Поиск с возвращением
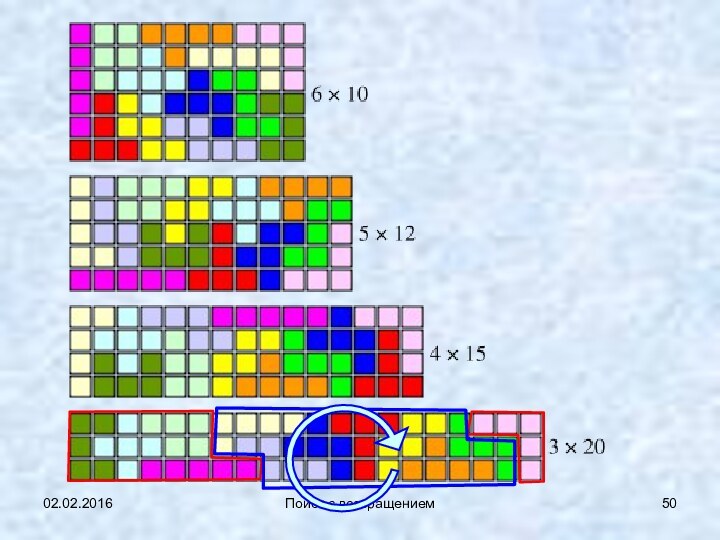
Для случая 6×10 эту задачу впервые
решил в 1965 году Джон Флетчер [1].
Существует ровно
2339 различных укладок пентамино в прямоугольник 6×10, не считая поворотов и отражений целого прямоугольника, но считая повороты и отражения его частей
(иногда внутри прямоугольника образуется симметричная комбинация фигур, поворачивая которую, можно получить дополнительные решения; для прямоугольника 3×20, приведённого на рисунке, второе решение можно получить поворотом блока из 7 фигур, или, иначе говоря, если поменять местами четыре фигуры, крайние слева, и одну крайнюю справа, см.предыдущий слайд).
Слайд 52
02.02.2016
Поиск с возвращением
Продолжение
Для прямоугольника 5×12 существует 1010 решений,
4×15 — 368 решений,
3×20 — всего 2 решения.
John
G. Fletcher (1965). "A program to solve the pentomino problem by the recursive use of macros". Communications of the ACM 8, 621–623.
Слайд 53
02.02.2016
Поиск с возвращением
Мартин Гарднер








![Построение и анализ алгоритмов. Поиск с возвратом. (Лекция 1) 02.02.2016Поиск с возвращениемПроверка s[k] bool noQueen (uns s, uns k) // ферзь](/img/tmb/15/1420017/abf69346bcaabec5a2f34cc20274828e-720x.jpg)
![Построение и анализ алгоритмов. Поиск с возвратом. (Лекция 1) 02.02.2016Поиск с возвращениемНахождение очередного свободного поля s[k]/*найти следующее наименьшее значение s[k],](/img/tmb/15/1420017/2b7731af566943ac778b01fc8a88e54d-720x.jpg)
![Построение и анализ алгоритмов. Поиск с возвратом. (Лекция 1) 02.02.2016Поиск с возвращениемРеализацияvoid queen1(const uns n){ pos s; /*s[k] - наименьший элемент множества](/img/tmb/15/1420017/c25bf83b7f20ecc6cfc3cfec7abe8e3a-720x.jpg)
![Построение и анализ алгоритмов. Поиск с возвратом. (Лекция 1) 02.02.2016Поиск с возвращениемwhile (k>0) { while ((k>=1) && (s[k]](/img/tmb/15/1420017/361cbdf37f53253d0a015e276442e0f9-720x.jpg)

![Построение и анализ алгоритмов. Поиск с возвратом. (Лекция 1) Усовершенствования02.02.2016Поиск с возвращениемvoid queen1(const uns n){pos s; //s[k] - наименьший элемент множества](/img/tmb/15/1420017/fba011faa353ca000e544e21cc390424-720x.jpg)