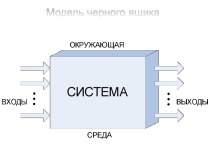
Слайд 2
Как представляются в компьютере целые числа?
Целые
числа могут представляться в компьютере со знаком или без
знака.
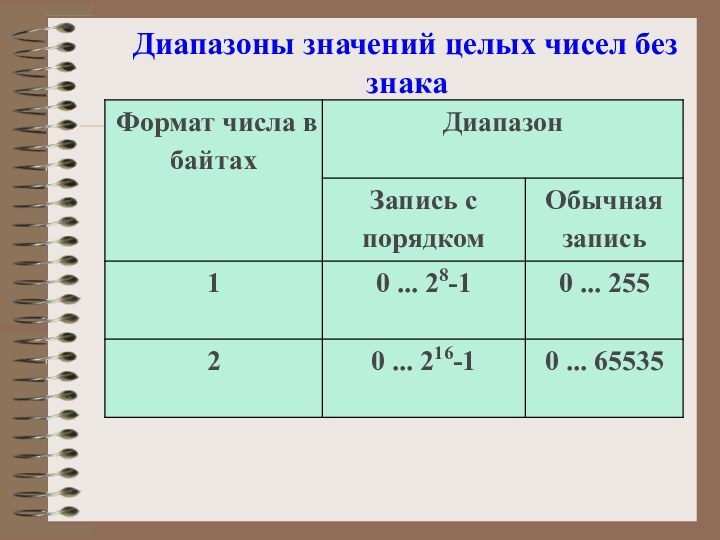
Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 000000002 до 111111112 , а в двубайтовом формате - от 00000000 000000002 до 11111111111111112.
Слайд 3
Диапазоны значений целых чисел без знака
Слайд 4
Число 3910 = 100111 2 в однобайтовом формате:
Число
3910 = 100111 2 в двубайтовом формате:
Число 65 53510
= 11111111 111111112 в двубайтовом формате:
Слайд 5
Целые числа со знаком
обычно занимают в памяти компьютера один, два
или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак "плюс" кодируется нулем, а "минус" - единицей.
Диапазоны значений целых чисел со знаком
Слайд 6
Рассмотрим особенности записи целых чисел со
знаком на примере однобайтового формата, при котором для знака
отводится один разряд, а для цифр абсолютной величины - семь разрядов.
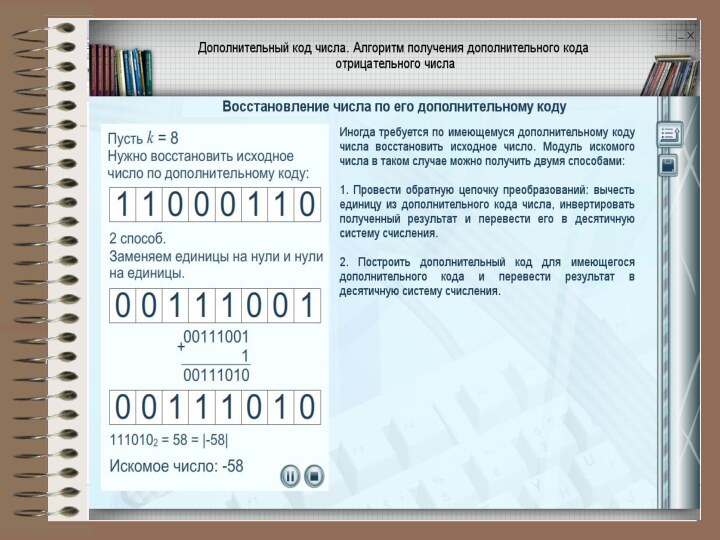
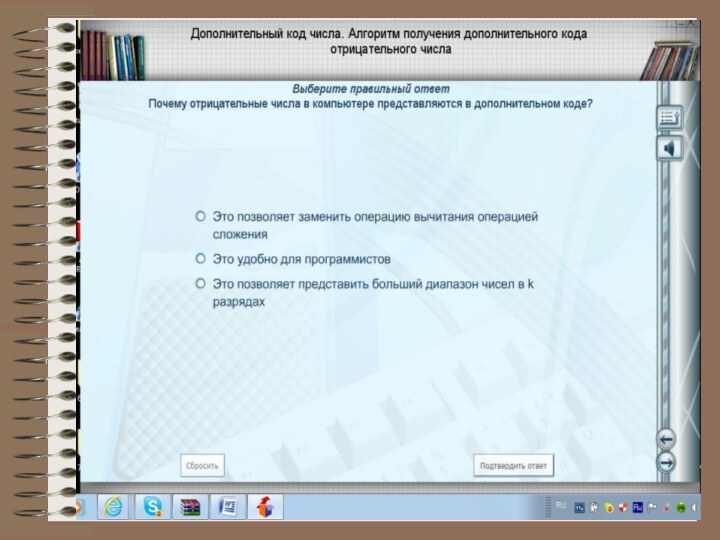
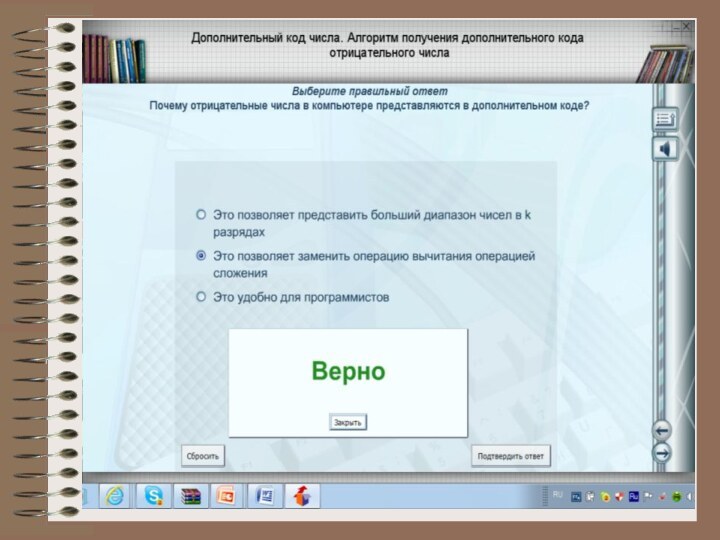
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.
Слайд 7
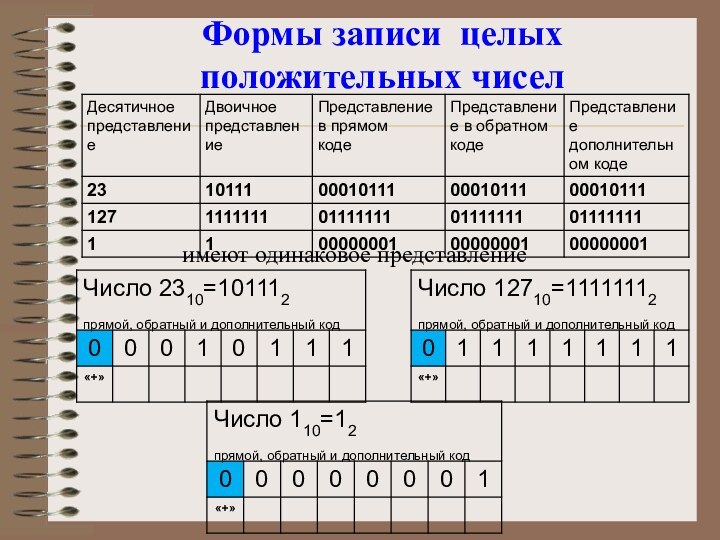
Положительные числа в прямом, обратном и дополнительном
кодах изображаются одинаково - двоичными кодами с цифрой 0
в знаковом разряде.
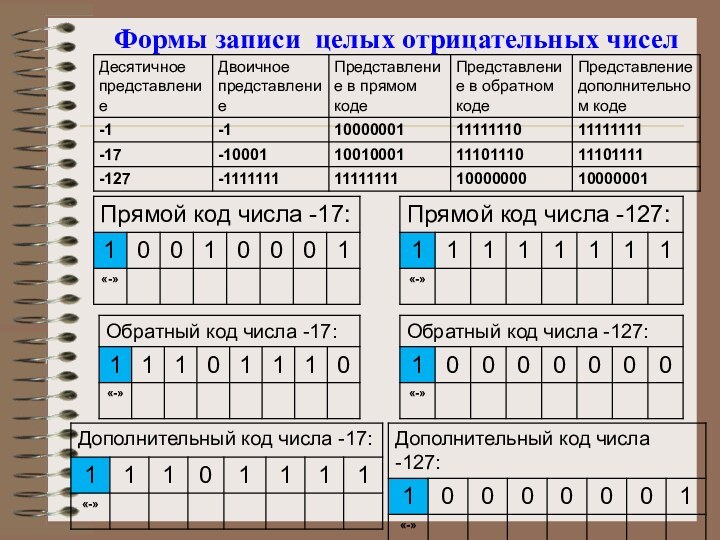
Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа - двоичный код его абсолютной величины
Слайд 8
2. Обратный код. Получается инвертированием всех
цифр двоичного кода абсолютной величины числа, включая разряд знака:
нули заменяются единицами, а единицы –нулями.
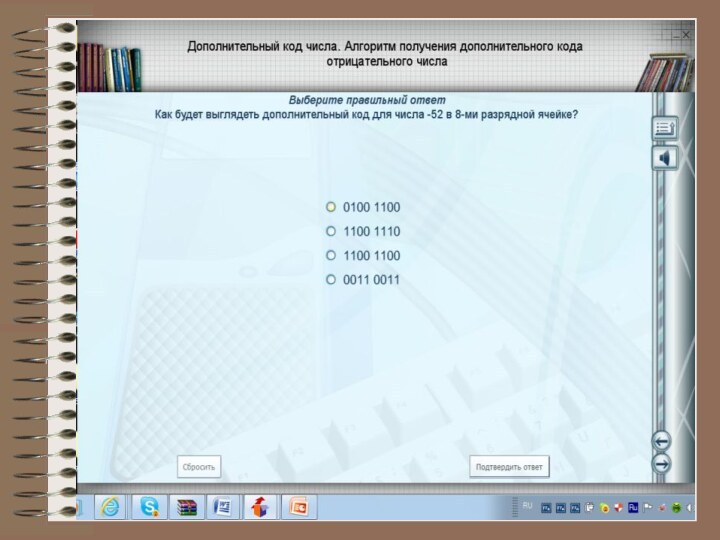
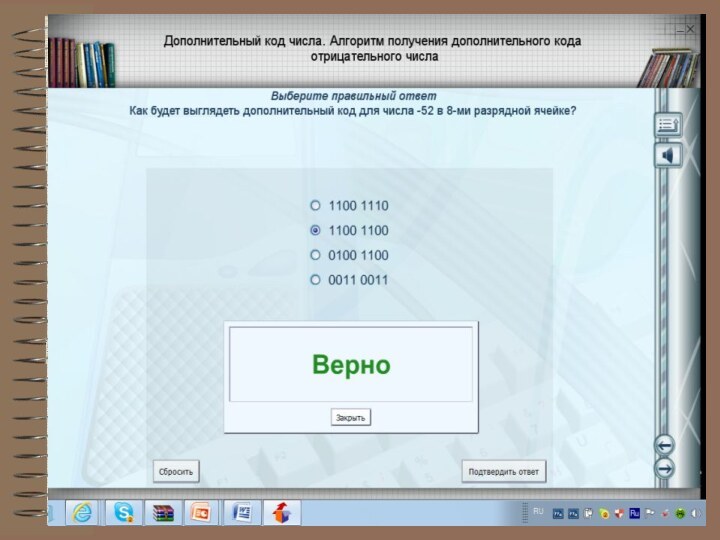
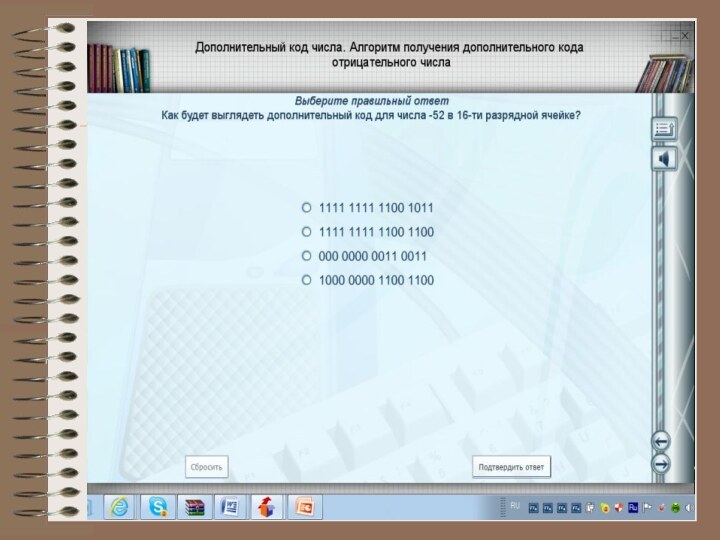
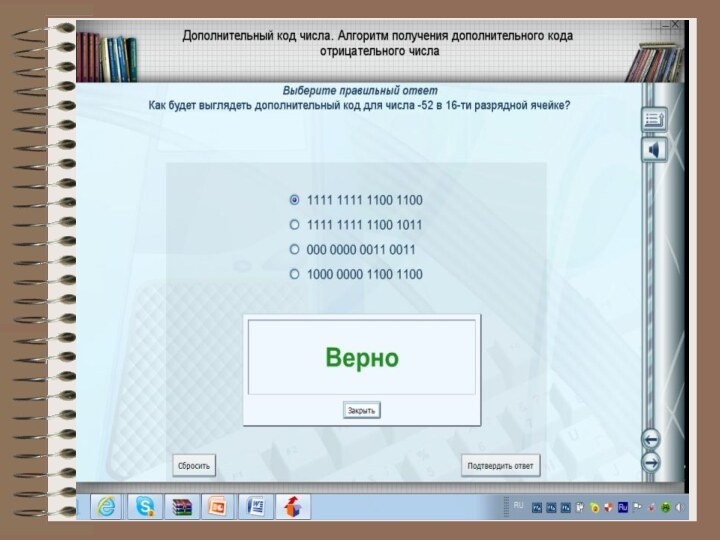
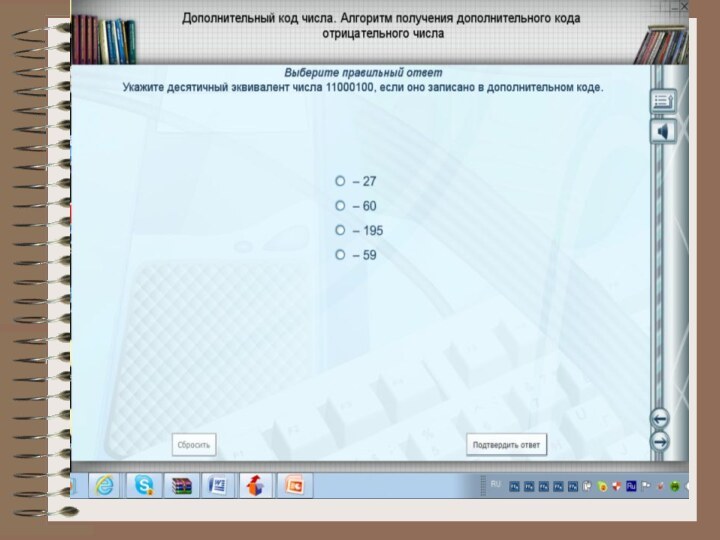
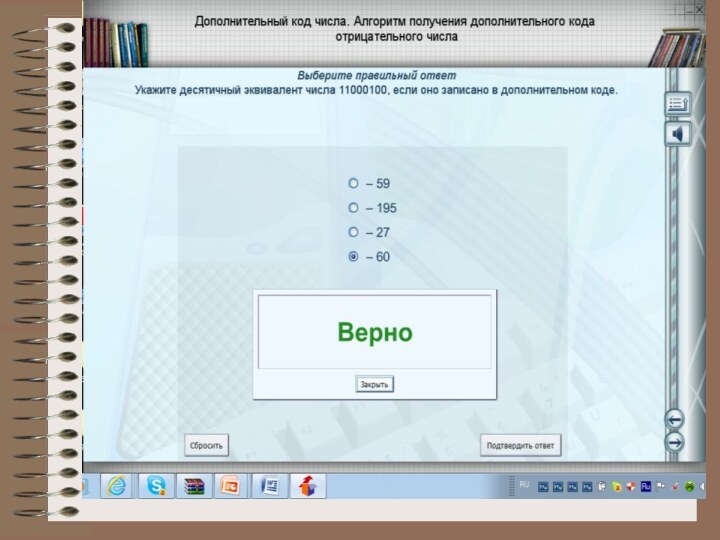
3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
Слайд 9
Формы записи целых положительных чисел
имеют одинаковое представление
Слайд 10
Формы записи целых отрицательных чисел
Слайд 11
Операции над числами с фиксированной точкой.
Слайд 12
1. А и В положительные. При
суммировании складываются все разряды, включая разряд знака. Так как
знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:
Получен правильный результат.
Слайд 13
2. А положительное, B отрицательное и
по абсолютной величине больше, чем А.
Например:
Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –710.
Слайд 14
3. А положительное, B отрицательное и
по абсолютной величине меньше, чем А. Например:
Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы!!!
Слайд 15
4. А и В отрицательные. Например:
Полученный первоначально неправильный результат (обратный код числа
–1110 вместо обратного кода числа –1010) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы.
При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –1010.
Слайд 16
5. А и В положительные, сумма
А+В больше, либо равна 2n–1, где n – количество
разрядов формата чисел (для однобайтового формата n=8, 2n–1 = 27 = 128). Например:
Семи разрядов цифровой части числового формата недостаточно для размещения восьмиразрядной суммы (16210 = 101000102), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака суммы и знаков слагаемых (знак суммы – отрицателен, знак слагаемых – положительный), что является свидетельством переполнения разрядной сетки.
Слайд 17
6. А и В отрицательные, сумма абсолютных величин
А и В больше, либо равна 2n–1.
Например:
632
=01111112
Здесь знак суммы тоже не совпадает со знаками слагаемых, что свидетельствует о переполнении разрядной сетки.
Слайд 18
1. А и В положительные. Здесь нет отличий
от случая 1, рассмотренного для обратного кода, т.к. дополнительный
код используется только для отрицательных чисел.
Слайд 19
2. А положительное, B отрицательное и по
абсолютной величине больше, чем А. Например:
Получен правильный результат в дополнительном коде.
При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –710.
Слайд 20
3. А положительное, B отрицательное и
по абсолютной величине меньше, чем А.
Например:
Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.
Слайд 21
4. А и В отрицательные.
Например:
Получен правильный результат в дополнительном коде.
Единицу переноса из знакового разряда компьютер отбрасывает. Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.
Слайд 22
Задача.
Выполнить действия над машинными кодами
чисел:
с фиксированной точкой. Формат 16 двоичных разрядов.
Дано: А=190;
В=250
Найти: С1=А + В; С2=А – В.
Решение:
А(10) = 190; А(16)=BE=10111110(2)
В(10) = 250; В(16)=FA=11111010(2)
С1 = А+В С2 = А – В
А= 0 000000010111110 А = 0 0000000010111110 (прямой код)
+В= 0 000000011111010 - В = 1 111111100000110
(дополнительный код)
С1= 0 000000110111000 С2 = 1 111111111000100
Проверка: Проверка:
С1=110111000(2) С2 = - 111100 = - BC= - 3*16 +12*1 =
= - 60 (10)
С1(16) = 1В8 = 1*16*16+11*16+8*1 = 440(10)
Ответ:
С1 = 0 000000110111000
С2 = 1 000000000111100
Слайд 23
Задача.
Выполнить действия над машинными кодами чисел:
с фиксированной точкой.
Формат 16 двоичных разрядов.
Дано: А= - 387; В=
- 128
Найти: С1=А + В;
Решение:
X = A+B X = (-A) + ( - B)
А(10) = - 387; А(16)=- 183(16)= - 110000011(2)
В(10) = - 128; В(16)=- 80(16)= - 10000000(2)
A(2) = 1 000000110000011 –прямой код
А(2) = 1 111111001111100 –обратный код
А(2) = 1 111111001111101 – дополн. код
Слайд 24
В(2) = 1 000000010000000 – прямой код
В(2) = 1
111111101111111 – обратный код
В(2) = 1 111111110000000 – дополн.код
(-А) = 1 111111001111101
+ (-В) = 1 111111110000000
Х = 1 111110111111101 –доп. код
Х = 1 000001000000010 – обр.код
Х = 1 000001000000011 – пр.код
Х = - 203(16) = - (2*16*16+0*16+3*1) =
= - (256*2+3) = - (512+3)+ - 515
Слайд 25
Представление чисел с плавающей точкой.
Этот
способ представления опирается на нормализованную (экспоненциальную) запись действительных чисел.
Нормализованная запись отличного от нуля действительного числа A - это запись вида:
А= m* qn,
где m – мантисса числа (правильная дробь, у которой первая цифра после запятой не равна нулю),
q – основание системы,
n – порядок числа.
Слайд 26
Примеры:
1. Мантисса числа 64.5 – это
число 0.645, а порядок – число 2, так как
64.5 = 0.645*10 степень (2).
2. Мантисса числа 0.0000012 – это число 0.12, а порядок – число -5, потому что 0.0000012= =0.12*10 степень(-5).
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы.
Слайд 27
Операции над числами с плавающей точкой.
Слайд 28
Дано:А = 12,75; В = 250
Найти: С3 =
А + В, С4 = А – В
Формат –
32 двоичных разряда со смещенным порядком.
А(10) = 12,75 = А(16) = С.С;
В(10) = 250 = В(16) = FA
Нормализация мантисс
mA = 0.CC; pxA = 40 + 1 = 41
mB = 0.FA; pxB = 40 + 2 = 42
Выравнивание характеристик:
∆p = pxA – pxB = -1
m*A = mA * 16 -1 = 0.0CC;
pxA = 41+ 1 = 42
C3 = A + B;
mA = 00 0CC000 pxA = 42
mB = 00 FA0000 pxB = 42
mC3 = 01 06C000 pxC = 42
Слайд 29
Нормализация мантиссы результата
mxC3 = 00 106C00;
pxC3 = 42 + 1 = 43
Проверка
С3(16) =
106,C = (C3) = 262,75
C3 = 0 1000011000100000110110000000000
C4 = A – B
mA = 00 0CC000 pxA = 42
mB = 10 06000 pxB = 42
mC3 = 10 12C000 pxC = 42
Нормализация мантиссы результата:
mС4 = 10 ED4000 pxC4 = 42
Проверка:
С4 = - ED.4 = (C4) = - (14 * 16 + 13 * 1 + 4/16) = - 237, 25
C4=11000010111011010100000000000000
Слайд 41
Задания на дом:
1. Угринович Н.Д. п. 2.9.,
стр.103-105.
2. Заполнить карточки.