Презентация на тему Системы распознавания образов

основан на моделировании гипотетического механизма человеческого мозга.

Структура модели

заранее постулируется. При таком подходе уровень биологических знаний или гипотез о биологических механизмах является исходной предпосылкой, на которой базируются модели этих механизмов.

Рис. 1

коэффициенты усиления v которых переменны и изменяются в процессе

обучения.
Взвешенные комбинации выходов R-элементов составляют реакцию системы, которая указывает на принадлежность распознаваемого объекта определенному образу.

совокупности сенсорных элементов S-элементов

S-элементы случайным образом связаны с совокупностью ассоциативных элементов А-элементов, выход которых отличается от нуля только тогда, когда возбуждено достаточно большое число S-элементов.

устанавливается только один R-элемент, который обладает двумя реакциями —

положительной и отрицательной.

Если образов больше двух, то для каждого образа устанавливают свой R-элемент, а выход каждого такого элемента представляет линейную комбинацию выходов A-элементов:

- реакция j-го R-элемента;

- реакция i-го A-элемента;

- вес связи от i-го A-элемента к j-му R-элементу;

- порог j-го R-элемента.

Аналогично записывается уравнение i-го A-элемента:

(1)

(2)

Сигнал yk может быть непрерывным, но чаще всего он принимает только два значения: 0 или 1. Сигналы от S-элементов подаются на входы А-элементов с постоянными весами равными 1, но каждый А-элемент связан
только с группой случайно выбранных S-элементов.

V1 и V2.

Будем считать, что в перцептроне существует

два R-элемента, один из которых предназначен образу V1, а другой — образу V2.

Перцептрон будет обучен правильно, если выход R1 превышает R2, когда распознаваемый объект принадлежит образу V1, и наоборот.

Разделение объектов на два образа можно провести и с помощью только одного R-элемента. Тогда объекту образа V1 должна соответствовать положительная реакция R-элемента, а объектам образа V2 — отрицательная.

принадлежащих образам V1 и V2.

В процессе обучения изменяются

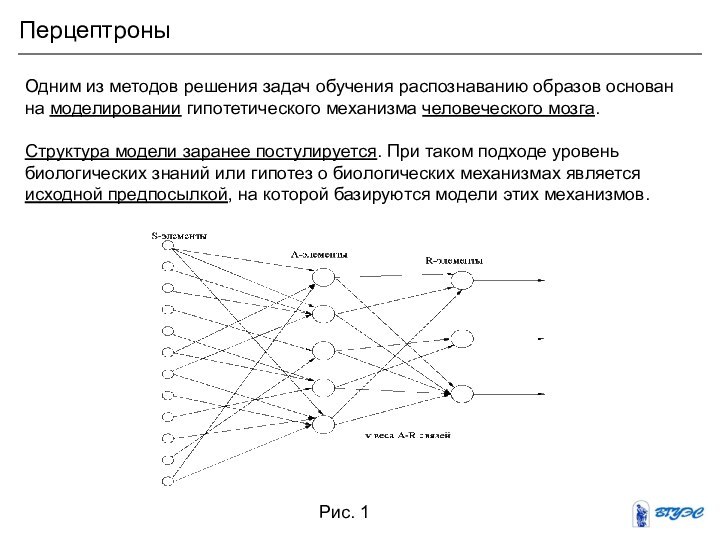
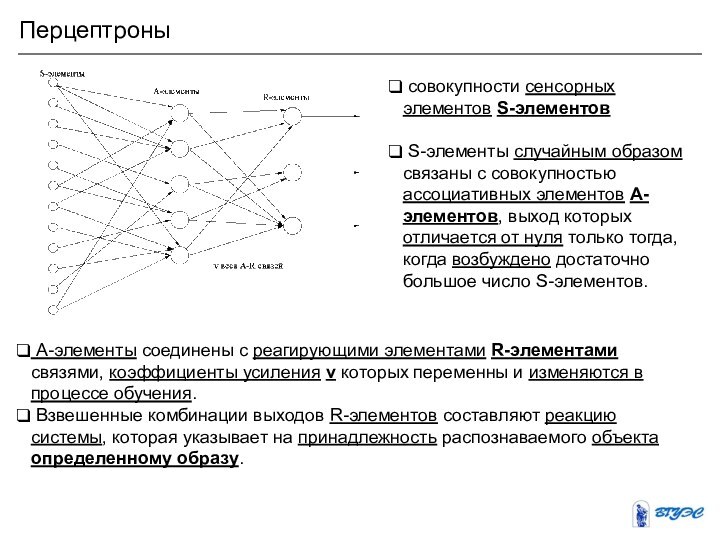
веса vi А-элементов. В частности, если применяется система подкрепления с коррекцией ошибок, прежде всего учитывается правильность решения, принимаемого перцептроном.

Если решение правильно, то веса связей всех сработавших А-элементов, ведущих к R-элементу, выдавшему правильное решение, увеличиваются, а веса несработавших А-элементов остаются неизменными.

Можно оставлять неизменными веса сработавших А-элементов, но уменьшать веса несработавших. В некоторых случаях веса сработавших связей увеличивают, а несработавших — уменьшают.

После процесса обучения перцептрон сам, без учителя, начинает классифицировать новые объекты.

Перцептроны

бинарных S-элементов к A-элементам и от A-элементов к единственному

R-элементу, то такой перцептрон принято называть элементарным альфа-перцептроном.

Обычно классификация C(W) задается учителем. Перцептрон должен выработать в процессе обучения классификацию, задуманную учителем.

Рис. 2. Элементарный -перцептрон

основополагающих теорем, две из которых, определяющие основные свойства перцептрона,

приведены ниже.

Теорема 1. Класс элементарных альфа-перцептронов, для которых существует решение для любой задуманной классификации, не является пустым.


Эта теорема утверждает, что для любой классификации обучающей последовательности можно подобрать такой набор (из бесконечного набора) А-элементов, в котором будет осуществлено задуманное разделение обучающей последовательности при помощи линейного решающего правила ).

решение существует, то в процессе обучения a -перцептрона с

коррекцией ошибок, начинающегося с произвольного исходного состояния, это решение будет достигнуто в течение конечного промежутка времени.


Смысл этой теоремы состоит в том, что если относительно задуманной классификации можно найти набор А-элементов, в котором существует решение, то в рамках этого набора оно будет достигнуто в конечный промежуток времени.

перцептрона с бесконечным числом А-элементов со всевозможными связями с

S-элементами (полный набор A-элементов).

В таких перцептронах решение всегда существует, а раз оно существует, то оно и достижимо в альфа-перцептронах с коррекцией ошибок.

Очень интересную область исследований представляют собой многослойные перцептроны и перцептроны с перекрестными связями, но теория этих систем практически еще не разработана.

Модель нейронной сети с обратным распространением ошибки (back propagation)

впервые исследована Дж. Маккалоком и У. Питтом.

В 1943

году вышла их работа "Логическое исчисление идей, относящихся к нервной деятельности", в которой была построена модель нейрона, и сформулированы принципы построения искусственных нейронных сетей.

Крупный толчок развитию нейрокибернетики дал американский нейрофизиолог Фрэнк Розенблатт, предложивший в 1962 году свою модель нейронной сети — перцептрон.

В 1982 году американский биофизик Дж. Хопфилд предложил оригинальную модель нейронной сети, названную его именем. В последующие несколько лет было найдено множество эффективных алгоритмов:
сеть встречного потока,
двунаправленная ассоциативная память и др.

В киевском институте кибернетики с 70-х годов ведутся работы над стохастическими нейронными сетями.

propagation)

В 1986 году Дж. Хинтон и его

коллеги опубликовали статью с описанием модели нейронной сети и алгоритмом ее обучения, что дало новый толчок исследованиям в области искусственных нейронных сетей.

Нейронная сеть состоит из множества одинаковых элементов — нейронов, поэтому начнем с них рассмотрение работы искусственной нейронной сети.

Биологический нейрон моделируется как устройство, имеющее несколько входов (дендриты), и один выход (аксон).

Каждому входу ставится в соответствие некоторый весовой коэффициент w, характеризующий пропускную способность канала и оценивающий степень влияния сигнала с этого входа на сигнал на выходе.

propagation)
В зависимости от конкретной реализации, обрабатываемые нейроном сигналы могут

быть аналоговыми или цифровыми (1 или 0).

В теле нейрона происходит взвешенное суммирование входных возбуждений, и далее это значение является аргументом активационной функции нейрона, один из возможных вариантов которой представлен на Рис. 3.

propagation)
Рис. 3. Искусственный нейрон
Будучи соединенными определенным образом, нейроны образуют

нейронную сеть. Работа сети разделяется на обучение и адаптацию.
Под обучением понимается процесс адаптации сети к предъявляемым эталонным образцам путем модификации (в соответствии с тем или иным алгоритмом) весовых коэффициентов связей между нейронами.

Заметим, что этот процесс является результатом алгоритма функционирования сети, а не предварительно заложенных в нее знаний человека, как это часто бывает в системах искусственного интеллекта.

propagation)
Среди различных структур нейронных сетей (НС) одной из наиболее

известных является многослойная структура, в которой каждый нейрон произвольного слоя связан со всеми аксонами нейронов предыдущего слоя или, в случае первого слоя, со всеми входами НС.

Такие НС называются полносвязными.

Когда в сети только один слой, алгоритм ее обучения с учителем довольно очевиден, так как правильные выходные состояния нейронов единственного слоя заведомо известны, и подстройка синаптических связей идет в направлении, минимизирующем ошибку на выходе сети.
По этому принципу строится, например, алгоритм обучения однослойного перцептрона.

всех слоев, кроме последнего, как правило, не известны, и

двух- или более слойный перцептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах НС.

Приемлемый вариант решения – распространение сигналов ошибки от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы.

Этот алгоритм обучения НС получил название процедуры обратного распространения. Именно он будет рассмотрен в дальнейшем.

Модель нейронной сети с обратным распространением ошибки (back propagation)

propagation)
Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС

является величина:

(3)

где

– реальное выходное состояние нейрона j выходного слоя N

нейронной сети при подаче на ее входы p-го образа;

– идеальное (желаемое)

выходное состояние этого нейрона.

Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам.
Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:

(4)

здесь

– весовой коэффициент синаптической связи, соединяющей i-ый нейрон слоя n-1 с j-ым нейроном слоя n; – коэффициент
скорости обучения, 0 < < 1.

propagation)
Как показано в [Розенблатт Ф. Принципы нейродинамики (перцептрон и

теория механизмов мозга).]

Здесь под , как и раньше, подразумевается выход нейрона j, а под – взвешенная сумма его входных сигналов, то есть аргумент активационной функции.
Так как множитель является производной этой функции по ее аргументу, из этого следует, что производная активационной функции должна быть определена на всей оси абсцисс.

(5)

прочие активационные функции с неоднородностями не подходят для рассматриваемых

НС.
В них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой. В случае гиперболического тангенса

Третий множитель

очевидно, равен выходу нейрона предыдущего слоя

(6)

Модель нейронной сети с обратным распространением ошибки (back propagation)

propagation)
Что касается первого множителя в (5), он легко раскладывается

следующим образом:

(7)

Здесь суммирование по k выполняется среди нейронов слоя n+1.
Введя новую переменную:

(8)

мы получим рекурсивную формулу для расчетов величин

слоя

n из величин

более старшего слоя n+1.

(9)

Для выходного же слоя:

(10)

propagation)
Теперь мы можем записать (4) в раскрытом виде:

(11)

Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (11) дополняется значением изменения веса на предыдущей итерации

(12)

где – коэффициент инерционности, t – номер текущей итерации.

propagation)
Таким образом, полный алгоритм обучения НС с помощью процедуры

обратного распространения ошибки строится так:

1. Подать на входы сети один из возможных образов и в режиме обычного функционирования НС, когда сигналы распространяются от входов к выходам, рассчитать значения последних. Напомним, что

(13)

где M – число нейронов в слое n-1 с учетом нейрона с постоянным выходным состоянием +1, задающего смещение;

– i - ый вход нейрона j слоя n.

где f() – сигмоид

(14)

(15)

где – q-ая компонента вектора входного образа.

propagation)
2. Рассчитать для выходного слоя

по формуле (10).

Рассчитать по формуле (11) или (12) изменения весов слоя N.

3. Рассчитать по формулам (9) и (11) (или (9) и (12)) соответственно и для всех остальных слоев, n = N-1, ..., 1 .

4. Скорректировать все веса в НС

(16)

5. Если ошибка сети существенна, перейти на шаг 1. В противном случае – конец.

propagation)
Рис. 4

propagation)
Сети на шаге 1 попеременно в случайном порядке предъявляются

все тренировочные образы, чтобы сеть, образно говоря, не забывала одни по мере запоминания других. Алгоритм иллюстрируется Рис. 4

Из выражения (11) следует, что когда выходное значение yi(n-1) стремится к нулю, эффективность обучения заметно снижается. При двоичных входных векторах в среднем половина весовых коэффициентов не будет корректироваться[3], поэтому область возможных значений выходов нейронов [0,1] желательно сдвинуть в пределы [-0.5,+0.5], что достигается простыми модификациями логистических функций. Например, сигмоид с экспонентой преобразуется к виду:

(17)