- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Системы счисления
Содержание
- 2. ОпределениеСистема счисле́ния — символический метод записи чисел, представление чисел с помощью письменных
- 3. Виды систем счисленияСистемы счисления подразделяются на: позиционныесмешанные
- 4. Позиционные системы счисленияВ позиционных системах счисления одна
- 5. Под позиционной системой счисления обычно понимается b-ричная система
- 6. Позиционные системы счисления Формула представления позиционных чисел:
- 7. Позиционные системы счисления Наиболее употребляемыми в настоящее время
- 8. Непозиционные системы счисленияВ непозиционных системах счисления величина,
- 9. Непозиционные системы счисленияКаноническим примером почти непозиционной системы
- 10. Двоичная система счисленияДвоичная система счисления — позиционная система счисления с
- 11. Двоичная система счисления ПроизношениеВо всех системах счисления (кроме
- 12. Двоичная система счисленияДвоичная система счисления является комбинацией двоичной
- 13. Преобразование десятичных чисел в двоичныеДопустим, нам нужно
- 14. Преобразование дробных десятичных чисел в двоичныеЕсли в
- 15. Преобразование дробных десятичных чисел в двоичныеТребуется перевести
- 16. Преобразование двоичных чисел в десятичныеДля преобразования из
- 17. Преобразование двоичных чисел в десятичныеДопустим, дано двоичное
- 18. Преобразование дробных двоичных чисел в десятичныеНужно перевести
- 19. Сложение, вычитание двоичных чиселТаблицы сложения и вычитанияПример сложения «столбиком» (1410 + 510 = 1910 или 11102 + 1012 = 100112):
- 20. Умножение двоичных чиселТаблица умноженияПример умножения «столбиком» (1410 * 510 = 7010 или 11102 * 1012 = 10001102):
- 21. Шестнадцатеричная система счисленияШестнадцатеричная система счисления — позиционная система
- 22. Шестнадцатеричная система счисленияПрименениеШироко используется в низкоуровневом программировании
- 23. Перевод чисел из десятичной в шестнадцатеричную системуПеревод
- 24. Перевод чисел из десятичной в шестнадцатеричную системуДля
- 25. Перевод чисел из 16-ой системы в 10-уюДля
- 26. Перевод чисел из 2-ой системы в 16-ую
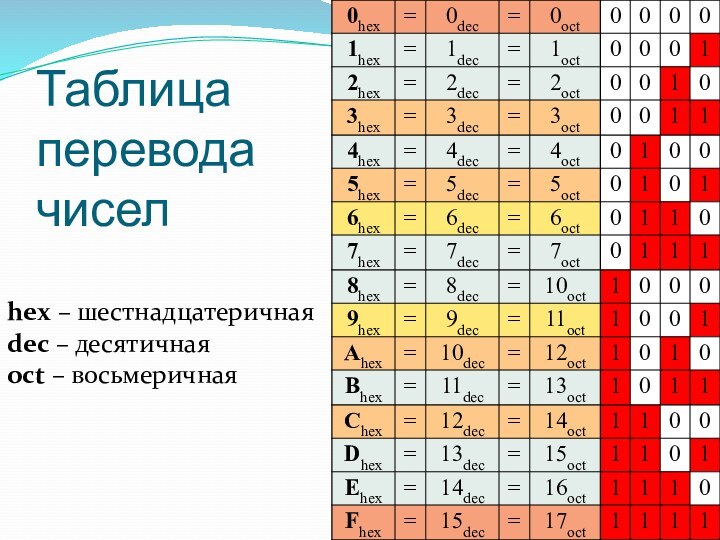
- 27. Таблица перевода чиселhex – шестнадцатеричнаяdec – десятичнаяoct – восьмеричная
- 28. Представление отрицательных чиселДополнительный код (англ. two’s complement) — наиболее
- 29. Представление отрицательных чиселПри записи числа в дополнительном
- 30. Представление отрицательных чиселДвоичное 8-ми разрядное число со знаком в
- 32. Преобразование в дополнительный кодПреобразуем отрицательное число −5,
- 33. Экспоненциальная записьЭкспоненциа́льная за́пись — представление действительных чисел в
- 34. Компьютерный способ экспоненциальной записиНа компьютере (в частности
- 35. Скачать презентацию
- 36. Похожие презентации
ОпределениеСистема счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.Система счисления:даёт представления множества чисел (целых и/или вещественных);даёт каждому числу уникальное представлениеотражает алгебраическую и арифметическую структуру чисел.


































Слайд 2
Определение
Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.
Система
счисления:
структуру чисел.
Слайд 4
Позиционные системы счисления
В позиционных системах счисления одна и
та же цифра в записи числа имеет различные значения в
зависимости от того места (разряда), где она расположена.К числу таких систем относится современная десятичная система счисления
В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.
Слайд 5 Под позиционной системой счисления обычно понимается b-ричная система счисления,
которая определяется целым числом b > 1, называемым основанием системы счисления.
Целое число без
знака в b-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа.Например, число сто три представляется в десятичной системе счисления в виде:
Позиционные системы счисления
Слайд 6
Позиционные системы счисления
Формула представления позиционных чисел:
где
ak — это целые числа, называемые цифрами, удовлетворяющие неравенству:
Каждая степень
bk в такой записи называется весовым коэффициентом разряда. Старшинство разрядов определяется значением показателя k (номером разряда).
Слайд 7
Позиционные системы счисления
Наиболее употребляемыми в настоящее время позиционными
системами являются:
2 — двоичная (в информатике, программировании)
3 — троичная
8 — восьмеричная
10 — десятичная (используется повсеместно)
12 — двенадцатеричная (счёт дюжинами)
13 — тринадцатеричная
16 —шестнадцатеричная (в программировании)
60 — шестидесятеричная (единицы
измерения времени, измерение углов и, в частности, координат, долготы и широты).
Слайд 8
Непозиционные системы счисления
В непозиционных системах счисления величина, которую
обозначает цифра, не зависит от положения в числе.
При
этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
Слайд 9
Непозиционные системы счисления
Каноническим примером почти непозиционной системы счисления
является римская, в которой в качестве цифр используются латинские
буквы: I — 1 V — 5 X — 10 L — 50 C — 100 D — 500 M — 1000Например, II = 1 + 1 = 2 здесь символ I обозначает 1 независимо от места в числе.
На самом деле, римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из неё, например:
IV = 4, в то время как: VI = 6
Слайд 10
Двоичная система счисления
Двоичная система счисления — позиционная система счисления с основанием
2.
В этой системе счисления числа записываются с помощью двух символов (0 и 1).
Чтобы не путать в какой системе счисления записано число, его снабжают указателем справа внизу.
Например, число в десятичной системе 510 будет в двоичной 1012.
Иногда двоичное число обозначают префиксом 0b (ноль b), например 0b101.
Слайд 11
Двоичная система счисления
Произношение
Во всех системах счисления (кроме десятичной)
знаки читаются по одному. Например число 1012 произносится «один ноль
один».Отрицательные двоичные числа обозначаются так же как и десятичные: знаком «−» перед числом.
Однако в вычислительной технике широко используется запись отрицательных двоичных чисел в дополнительном коде, что может вносить путаницу.
Например число −510 может быть записано как −1012 но в компьютере будет храниться как:
11111111 11111111 11111111 111110112 (в 4 байтах)
Слайд 12
Двоичная система счисления
Двоичная система счисления является комбинацией двоичной системы
кодирования и показательной весовой функции с основанием 2.
Положительные целые числа
(без знака) записываются в виде суммы степеней двойки от 0 до числа n-1:49 = 1 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 110001
Слайд 13
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести
число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19
/2 = 9 с остатком 1
9 /2 = 4 c остатком 1
4 /2 = 2 без остатка 0
2 /2 = 1 без остатка 0
1 /2 = 0 с остатком 1Делим каждое частное на 2 и записываем остаток в конец двоичной записи.
Продолжаем деление до тех пор, пока в частном не будет 0.
Результат записываем справа налево. То есть нижняя цифра (1) будет самой левой и т.д.
В результате получаем число 19 в двоичной записи: 10011.
Слайд 14
Преобразование дробных десятичных чисел в двоичные
Если в исходном
числе есть целая часть то она преобразуется отдельно от
дробной.Дробь умножается на основание двоичной системы счисления (2)
В полученном произведении выделяется целая часть, которая принимается в качестве старшего разряда числа в двоичной системе счисления;
Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются над дробной частью произведения.
Слайд 15
Преобразование дробных десятичных чисел в двоичные
Требуется перевести дробное
десятичное число 15,2510 в дробное двоичное число.
Тогда нужно отдельно перевести
целую часть и отдельно – дробную.Дробную часть 0,25 умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
Ответ: 15,2510 = 1111,012
Слайд 16
Преобразование двоичных чисел в десятичные
Для преобразования из двоичной
системы в десятичную используют следующую таблицу степеней основания 2:
Начиная
с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.
Слайд 17
Преобразование двоичных чисел в десятичные
Допустим, дано двоичное число 1100012.
Для перевода в десятичное запишите его как сумму по
разрядам следующим образом:1 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 49
То же самое чуть иначе:
1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 49
То есть:
32 + 16 + 1 = 49
Слайд 18
Преобразование дробных двоичных чисел в десятичные
Нужно перевести число 1011010,1012 в
десятичную систему. Запишем это число следующим образом:
1*26 + 0*25 + 1*24 + 1*23 + 0*22 + 1*21 + 0*20 + 1*2-1 + 0*2-2 + 1*2-3 =
90,625То же самое чуть иначе:
1*64 + 0*32 + 1*16 + 1*8 + 0*4 + 1*2 + 0*1 + 1*0,5 + 0*0,25 + 1*0,125 = 90,625
То есть:
64 + 16 + 8 + 2 + 0,5 + 0,125 = 90,625
Слайд 19
Сложение, вычитание двоичных чисел
Таблицы сложения и вычитания
Пример сложения
«столбиком» (1410 + 510 = 1910 или 11102 + 1012 = 100112):
Слайд 20
Умножение двоичных чисел
Таблица умножения
Пример умножения «столбиком» (1410 * 510 =
7010 или 11102 * 1012 = 10001102):
Слайд 21
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления — позиционная система счисления по
целочисленному основанию 16.
Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от
0 до 9 и латинские буквы от A до F для обозначения цифр от 1010до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Слайд 22
Шестнадцатеричная система счисления
Применение
Широко используется в низкоуровневом программировании и
компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти
является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.
Слайд 23
Перевод чисел из десятичной в шестнадцатеричную систему
Перевод осуществляется
так же, как и в двоичной системе, но с
основанием 16.Переведём число 56,56710 в шестнадцатеричное:
Остаток от деления записываем в обратном порядке.
Получаем 5610 = 03816
Слайд 24
Перевод чисел из десятичной в шестнадцатеричную систему
Для перевода
дробной части числа последовательно умножаем дробную часть на основание
16. В результате каждый раз записываем целую часть произведения.0.567*16 = 9.072 (целая часть 9)
0.072*16 = 1.152 (целая часть 1)
0.152*16 = 2.432 (целая часть 2)
0.432*16 = 6.912 (целая часть 6)
Получаем 0.567 = 912616
Таким образом, число 56,56710 в шестнадцатеричной системе счисления записывается как 38,912616.
Слайд 25
Перевод чисел из 16-ой системы в 10-ую
Для перевода
шестнадцатеричного числа в десятичное необходимо это число представить в
виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316 = 3·160+10·161+5·162 = 3·1+10·16+5·256 = 3+160+1280
= 144310
Слайд 26 Перевод чисел из 2-ой системы в 16-ую и
наоборот
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно
разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведенной таблицы перевода.
Например:
0101101000112 = 0101 1010 0011 = 5A316
Слайд 28
Представление отрицательных чисел
Дополнительный код (англ. two’s complement) — наиболее распространённый
способ представления отрицательных целых чисел в компьютерах.
Он позволяет заменить операцию вычитания
на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ.Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение), либо вычитанием числа из нуля.
Слайд 29
Представление отрицательных чисел
При записи числа в дополнительном коде
старший разряд является знаковым.
Если его значение равно 0,
то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Слайд 30
Представление отрицательных чисел
Двоичное 8-ми разрядное число со знаком в дополнительном
коде может представлять любое целое в диапазоне от −128
до +127.Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно , что равно 127.
Слайд 32
Преобразование в дополнительный код
Преобразуем отрицательное число −5, записанное
в прямом коде, в дополнительный.
Прямой код числа −5,
взятого по модулю:101
Инвертируем все разряды числа, получая таким образом обратный код:
010
Добавим к результату 1:
011
Допишем слева знаковый единичный разряд:
1011
Слайд 33
Экспоненциальная запись
Экспоненциа́льная за́пись — представление действительных чисел в виде
мантиссы и порядка. Удобна при представлении очень больших и очень
малых чисел, а также для унификации их написания.N = M * np, где
N — записываемое число;
M — мантисса;
n — основание показательной функции;
p (целое) — порядок;
np — характеристика числа.
Пример:
1 000 000 (один миллион): 1,0 * 106
N = 1 000 000, M = 1,0, n = 10, p = 6
Слайд 34
Компьютерный способ экспоненциальной записи
На компьютере (в частности в
тексте компьютерных программ) экспоненциальную запись записывают в виде MEp, где:
M —
мантисса,E (exponent) — буква E, означающая «*10^» («…умножить на десять в степени…»)
p — порядок.
Например:





























