Слайд 2
Ограниченность классической логики для выражения свойств динамических объектов
(изменяющихся во времени)
Классическая логика высказываний (propositional logic)
Примитивная модель истины:
“черно-белая” модель, высказывания статичны, неизменны во времени
В обычной логике высказываний адекватно не формализуются предложения, в которых явно или не явно присутствуют свойства, истинность которых изменяется со временем:
Путин - президент России (истинно только в какой-то период)
Мы не друзья, пока ты не извинишься
Если m поступило на вход в канал, то потом m появится на выходе
Запрос к лифту c произвольного этажа, поступивший в любой момент времени, будет когда-нибудь в будущем удовлетворен
Мы хотим изучать и верифицировать системы, развивающиеся во времени, а обычная классическая логика неадекватна для выражения их свойств!
.
Темпоральные логики
Слайд 3
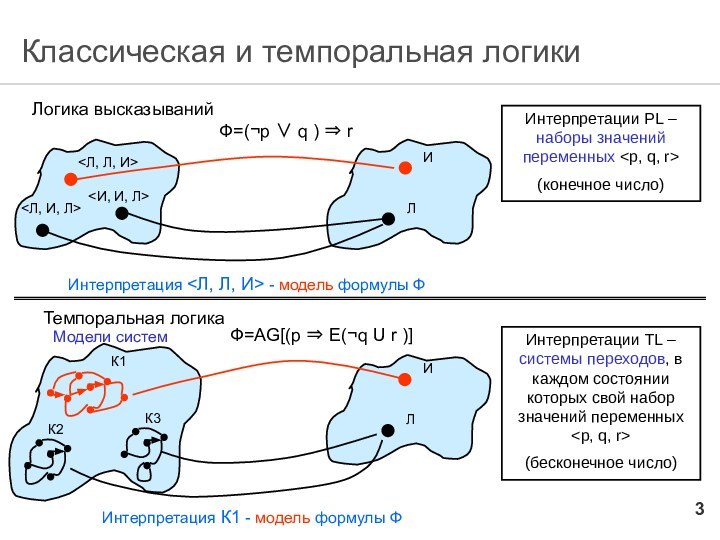
Классическая и темпоральная логики
Логика высказываний
Ф=(¬p ∨ q )
⇒ r
Темпоральная логика
Ф=AG[(p ⇒ E(¬q U r
)]
Интерпретации PL – наборы значений переменных
(конечное число)
Интерпретации TL – системы переходов, в каждом состоянии которых свой набор значений переменных
(бесконечное число)
Модели систем
Слайд 5
Дополнительные модальности TL: Until, neXt
F и G выражаются
через U: Fp ≡ true U p,
Gp ≡
¬F¬p
X (Next time)
Хp истинно в момент t, если p истинно в следующий момент времени (если считать моменты времени дискретными, то в момент t+1)
Примечание. Нам не важно в какой именно момент времени случится событие. Действительно, так как мы проверяем систему на наличие ошибок, нам не важно в какой именно момент времени может произойти ошибка, важно исключить любую возможность ее возникновения вообще. Также стоит признать очевидным тот факт, что прошлое при анализе технических систем менее важно, чем будущее.
Слайд 6
Linear Temporal Logic (LTL)
Формальное определение темпоральной логики
Формула φ
LTL это :
атомарное утверждение (атомарный предикат)
p, q, ...,
или Формулы, связанные логическими операторами ∨, ¬
или Формулы, связанные темпоральными операторами U, X
Прошлое обычно не рассматривают
Другие темпоральные операторы :
Fp = true U p
Gp = ¬F ¬p
Грамматика: φ ::= p | φ1∨ φ2 | ¬φ | Xφ | φ1 U φ2 | Fφ | G φ
Слайд 7
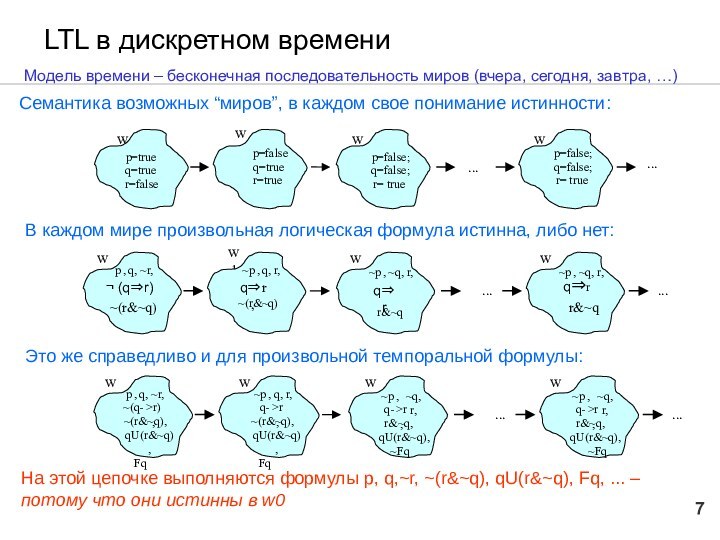
LTL в дискретном времени
На этой цепочке выполняются формулы
p, q,~r, ~(r&~q), qU(r&~q), Fq, ... – потому что
они истинны в w0
Семантика возможных “миров”, в каждом свое понимание истинности:
В каждом мире произвольная логическая формула истинна, либо нет:
Это же справедливо и для произвольной темпоральной формулы:
Модель времени – бесконечная последовательность миров (вчера, сегодня, завтра, …)
Слайд 8
Примеры формализация высказываний в LTL
“Dum spiro, spero” -
пока живу – надеюсь
G(я_живу ⇒ я_надеюсь)
“Мы придем к победе
коммунистического труда!”
F коммунистический_труд_победил!
“Сегодня он играет джаз, а завтра Родину продаст!”
он_играет_джаз ⇒ Xон_продает_Родину – слишком буквально
G(он_играет_джаз ⇒ FXон_продает_Родину)
“Раз Персил – всегда Персил”
G(Персил ⇒ GПерсил) – раз попробовав, будешь использовать всегда
“Мы не друзья, пока ты не извинишься”
¬Мы_друзья U Ты_извиняешься ∨ G(¬ Мы_друзья &¬Ты_извиняешься)
Слайд 9
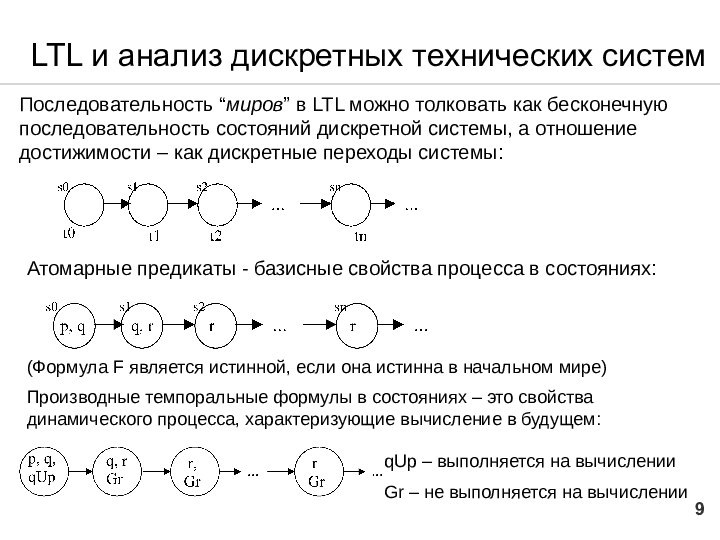
LTL и анализ дискретных технических систем
Последовательность “миров” в
LTL можно толковать как бесконечную последовательность состояний дискретной системы,
а отношение достижимости – как дискретные переходы системы:
Атомарные предикаты - базисные свойства процесса в состояниях:
(Формула F является истинной, если она истинна в начальном мире)
Производные темпоральные формулы в состояниях – это свойства динамического процесса, характеризующие вычисление в будущем:
qUp – выполняется на вычислении
Gr – не выполняется на вычислении
Слайд 10
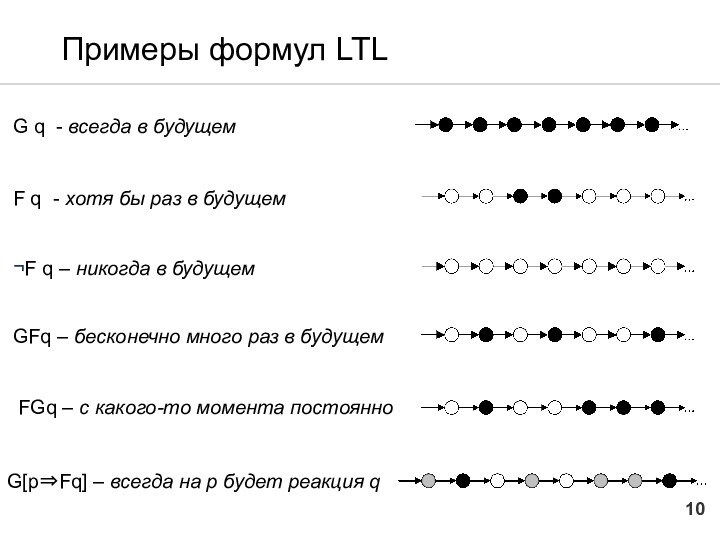
Примеры формул LTL
G q - всегда в будущем
F
q - хотя бы раз в будущем
¬F q
– никогда в будущем
GFq – бесконечно много раз в будущем
FGq – с какого-то момента постоянно
G[p⇒Fq] – всегда на р будет реакция q
Слайд 11
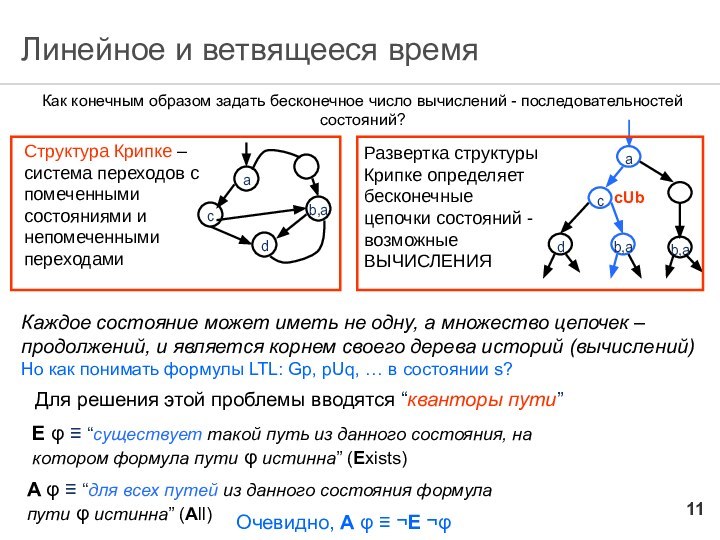
Линейное и ветвящееся время
Cтруктура Крипке –система переходов с
помеченными состояниями и непомеченными переходами
Развертка структуры Крипке определяет бесконечные
цепочки состояний - возможные ВЫЧИСЛЕНИЯ
Каждое состояние может иметь не одну, а множество цепочек – продолжений, и является корнем своего дерева историй (вычислений)
Но как понимать формулы LTL: Gp, pUq, … в состоянии s?
Для решения этой проблемы вводятся “кванторы пути”
Е φ ≡ “существует такой путь из данного состояния, на котором формула пути φ истинна” (Еxists)
А φ ≡ “для всех путей из данного состояния формула пути φ истинна” (All)
Очевидно, А φ ≡ ¬Е ¬φ
Как конечным образом задать бесконечное число вычислений - последовательностей состояний?
cUb
Слайд 12
Логика ветвящегося времени – CTL*
Возможные
формулы CTL* : A [(pUr)∨(qUr)], A [ Xp∨XXr ],
EGFp
Грамматика СTL* :
- Формулы состояний φ ::= р |¬φ | φ ∨ φ | Е α | Aα
Формулы путей α ::= φ | αUα | Xα
формула φ состояния s является формулой пути σ, если это состояние s является начальным состоянием пути σ
Темпоральные логики ветвящегося времени рассматривают возможные вычисления (пути на дереве) - траектории на развертке структуры Крипке
СTL* – Computational Tree Logic* - это одна из возможных логик ветвящегося времени
Базис CTL* = {¬, ∨, U, X, E}
Очевидно формула пути имеет смысл, только если зафиксирован путь.
В состояниях могут стоять только формулы состояний.
Слайд 13
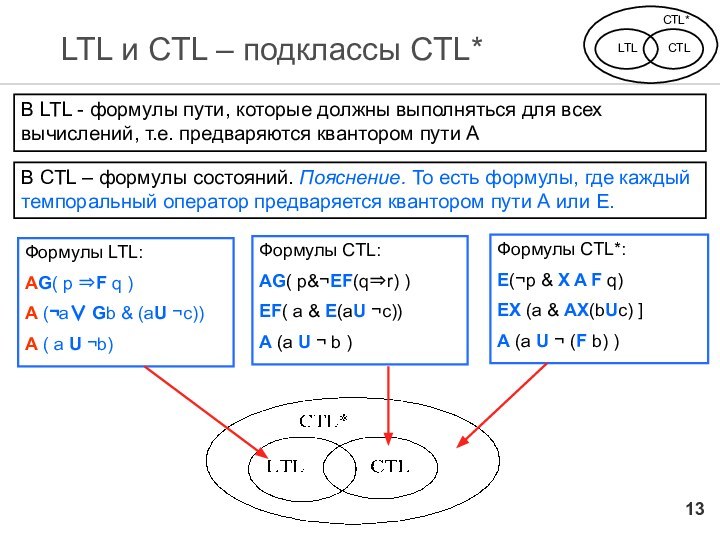
Формулы LTL:
AG( p ⇒F q )
А (¬а∨ Gb
& (aU ¬c))
А ( a U ¬b)
Формулы СTL:
AG(
p&¬EF(q⇒r) )
EF( а & E(aU ¬c))
A (a U ¬ b )
Формулы СTL*:
Е(¬p & X A F q)
ЕX (а & AX(bUc) ]
А (a U ¬ (F b) )
LTL и CTL – подклассы CTL*
В LTL - формулы пути, которые должны выполняться для всех вычислений, т.е. предваряются квантором пути А
В CTL – формулы состояний. Пояснение. То есть формулы, где каждый темпоральный оператор предваряется квантором пути А или Е.
Слайд 14
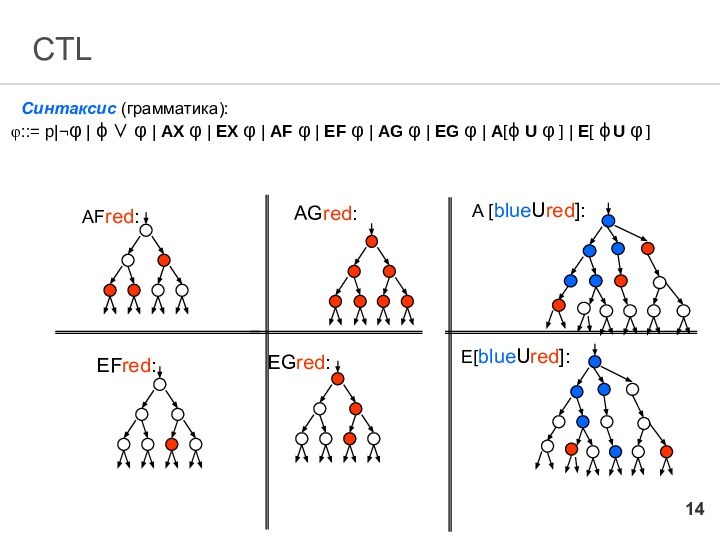
CTL
Синтаксис (грамматика):
::= p|¬φ | ϕ ∨ φ
| AX φ | EX φ | AF φ
| EF φ | AG φ | EG φ | A[ϕ U φ ] | E[ ϕ U φ ]
Слайд 15
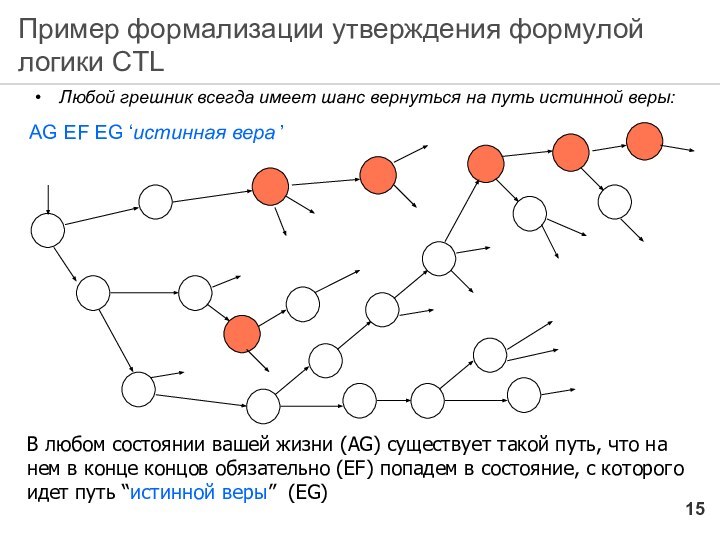
Пример формализации утверждения формулой логики CTL
Любой грешник всегда
имеет шанс вернуться на путь истинной веры:
В любом состоянии
вашей жизни (AG) существует такой путь, что на нем в конце концов обязательно (ЕF) попадем в состояние, с которого идет путь “истинной веры” (EG)
AG EF EG ‘истинная вера ’
Слайд 16
Выражение свойств технических систем в логике ветвящегося времени
CTL
AGAF Restart
при любом функционировании системы (на любом
пути) из любого состояния системы всегда обязательно вернемся в состояние рестарта
¬EF( int >0.01)
не существует такого режима работы прибора, при котором интенсивность облучения пациента превысит 0.01 радиан в сек
AG(antiFire_is_on ⇒ P captain_Permission)
в любом режиме, если противопожарная система включается, то на это обязательно предварительно была получена санкция капитана
AG (req3 ⇒ (req3 U ack))
во всех режимах после того, как запрос req3 установится, он никогда не будет снят, пока на него не придет подтверждение
E[ p U A [q U r] ]
cуществует режим, в котором условие p будет истинным с начала вычисления до тех пор, пока q не станет непрерывно активно до выполнения r
Слайд 17
Выражение свойств технических систем в логике ветвящегося времени
CTL
EF(Start & ¬Ready)
существует путь, на котором достижимо
состояние, где Start выполняется, а Ready – нет
AG(Req ⇒AF Answ)
на любой полученный запрос Req всегда в будущем получим ответ Answ
AG[q ⇒ AX[A(¬p U r) ∨ AG ¬r] ]
между q и r свойство р никогда не выполнится
Примечание. Темпоральная логика является расширением классической. То есть все тавтологии КИВ истины также и в ней.
Слайд 18
Приступая к моделированию
В методе верификации Model Checking в
качестве спецификации системы используется структура Крипке. Что же представляет
собой эта структура?
Структура Крипке М это пятерка М =(S, S0, R, L, AP)
S – конечное непустое множество состояний модели.
S0 ⊆ S – множество начальных состояний модели.
R ⊆ S × S – отношение переходов между состояниями,
обладающее свойством тотальности, т.е. ∀s ∈ S ∃t ∈ S ((s, t) ∈ R (Из любого состояния есть переход).
AP – конечное множество атомарных предикатов модели программы. (Атомарным предикатом может быть например утверждение «х равно 5»)
L: S→ 2^ |AP| – функция пометок (каждому состоянию отображение L сопоставляет множество истинных на нем атомарных предикатов).
Слайд 19
Структура Крипке
Вычислением σ структуры Крипке M называется любая

бесконечная последовательность σ = q0 q1 q2 … такая
что q0 ⊆ S0, и для любого неотрицательного i справедливо (q i, q i+1) ⊆ R. Формально вычисление структуры Крипке можно представить как отображение натурального ряда в множество состояний структуры. Таким образом σ(i) это какое-то состояние структуры Крипке.
Траекторией структуры Крипке соответствующей вычислению σ называется бесконечная цепочка L(σ) = L(q0) L(q1) L(q2) … То есть бесконечная цепочка подмножеств атомарных предикатов, истинных в соответствующих состояниях σ. Формально траектория – это отображение натурального ряда в 2^ |AP|.
Мы будем моделировать динамические системы в виде определенных структур Крипке.
Примечание. Стоит отметить что модель всегда проще реальной системы, она строится с помощью абстрагирования, отбрасывания части параметров, характеристик, особенностей реальной системы. Не смотря на это, важно, чтобы модель сохранила существенные черты исходной системы.
Слайд 20
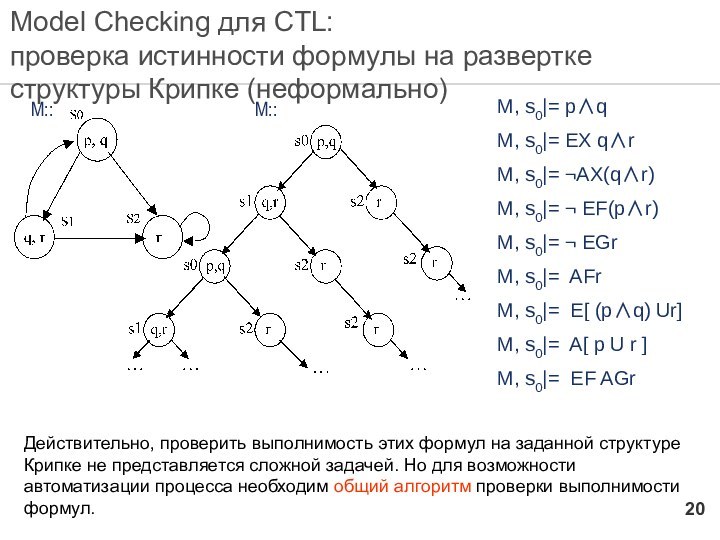
Model Checking для CTL:
проверка истинности формулы на развертке
структуры Крипке (неформально)
М, s0|= p∧q
М, s0|= EX q∧r
М, s0|=
¬AX(q∧r)
М, s0|= ¬ EF(p∧r)
М, s0|= ¬ EGr
М, s0|= AFr
М, s0|= E[ (p∧q) Ur]
М, s0|= A[ p U r ]
М, s0|= EF AGr
Действительно, проверить выполнимость этих формул на заданной структуре Крипке не представляется сложной задачей. Но для возможности автоматизации процесса необходим общий алгоритм проверки выполнимости формул.
Слайд 21
Базис CTL.
Примечание. Формулы темпоральной логики φ и ψ
называются семантически эквивалентными (обозначается φ ≡ ψ), если они
принимают одинаковые истинностные значения на каждой возможной интерпретации (структуре Крипке).
Для того, чтобы наш алгоритм был более простым нам нужно определиться с базисом. Пусть это будет например тройка { EX, AF, EU }
Покажем, что остальные 5 комбинаций можно выразить через эти 3:
AXφ ≡ ¬EX¬φ
EGφ ≡ ¬AF¬φ
A(φ1Uφ2) ≡ AFφ2 ∧ ¬E(¬φ2 U (¬φ1 ∧ ¬φ2 ) )
EFφ = E(True U φ)
AGφ ≡ ¬EF¬φ
Мы опустим доказательство того, что ни одна из комбинаций {EX,AF,EU} не выражается через 2 оставшиеся.
Слайд 22
Алгоритм маркировки
Пусть задана произвольная формула Ф логики CTL
и структура Крипке M. Для каждой подформулы ψ формулы
Ф алгоритм маркировки выполняет следующие шаги:
Вычисляется множество Sψ состояний структуры Крипке M, в которых выполняется ψ.
Вводится новый атомарный предикат pψ.
Этим атомарным предикатом помечаются все состояния из Sψ.
Поскольку обработка каждой формулы ψ заканчивается введением нового атомарного предиката pψ, и маркировкой этим предикатом всех состояний, на которых выполняется формула, то можно считать, что на каждом шаге алгоритма элементами подформул являются только атомарные предикаты. По завершении алгоритма, если начальное состояние структуры Крипке M помечено атомарным предикатом pφ, формула Ф выполняется на M.
Примечание. Код реализации алгоритма мы приводить не будем. Отметим лишь, что на каждом шаге алгоритма мы должны проводить синтаксический анализ формулы, для выявления очередных подформул с заданной глубиной.
Слайд 23
Маркировка состояний для формул AF,EX,EU
Маркировка состояний в случаях

конъюнкции, дизъюнкции, импликации и отрицания очевидна. Рассмотрим случаи с
AF, EX, EU:
Множество состояний, на которых выполняется EXp, строится из тех состояний, хотя бы один из преемников которых уже помечен p.
Множество состояний Y, на которых выполняется AFp, строится в два этапа. Сначала в Y собираются те состояния, которые уже помечены p (не забываем, что настоящее – часть будущего). Затем в Y добавляются состояния, все преемники которых уже принадлежат Y. Этот шаг повторяется многократно до тех пор, пока в Y можно добавить хотя бы одно новое состояние.
Множество состояний Y, на которых выполняется E(pUq), также выполняется в два этапа. Сначала в множество Y собираются те состояния, которые помечены q, в этих состояниях выполняется E(pUq), поскольку в них истинно q. Затем в Y добавляются те состояния, помеченные p, у которых хотя бы один преемник уже принадлежит Y. Этот шаг повторяется до тех пор, пока в Y добавляется хотя бы одно новое состояние.
Слайд 24
Свойства системы
Система
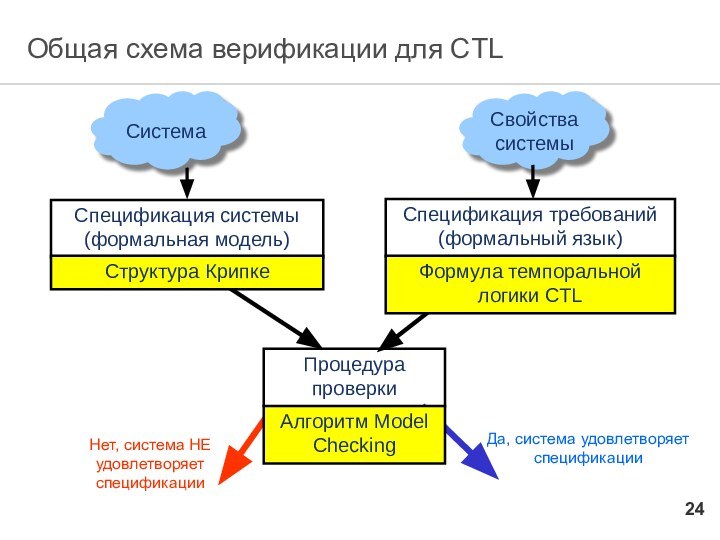
Общая схема верификации для СTL
Спецификация системы (формальная
модель)
Процедура проверки
Спецификация требований (формальный язык)
Формула темпоральной логики CTL
Структура Крипке
Да, система удовлетворяет спецификации
Нет, система НЕ
удовлетворяет спецификации
Алгоритм Model Checking
Слайд 25
Демонстрационный пример.
Задача – анализ поведения СВЧ печи
Требуется создать
и верифицировать систему, которая представляет собой логику “поведения” СВЧ
печи. При этом система должна удовлетворять следующему требованию:
Ни при каких обстоятельствах не должно работать излучение СВЧ печи при открытой дверце. (Важность этого требования очевидна).
Примечание. Конечно реальная система печи должна удовлетворять и другим требованиям, мы же сформулировали только одно, так как для нас сейчас важно познакомиться с методом верификации, а не разработать систему.
Слайд 26
Формализация системы. Выбираем AP
Сначала выберем множество атомарных предикатов.
Пусть это будут следующие предикаты:
st (start) = «кнопка
пуск нажата»
cd (close door) = «дверца печи закрыта»
ht (heating) = «излучение включено»
er (error) = «печь выдает сообщение об ошибке»
Примечание. Очевидно, что можно обойтись без предиката error - ни что не мешает нам запрограммировать печь так, чтобы в случае возникновения ошибки она никак не оповещала об этом пользователя.
Слайд 27
Формализация системы.
Теперь будем разбираться в системе, параллельно
дополняя соответствующую ей структуру Крипке.
Наш пользователь открыл упаковку,
прочитал инструкцию, установил печь, и подключил ее к электросети.
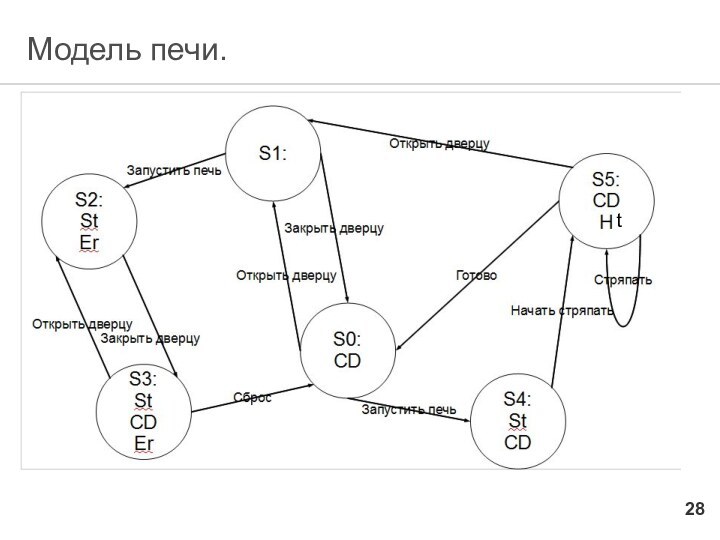
В этот момент печь находится в состоянии s0 в котором истинным является только 1 атомарный предикат, а именно cd (close door).
Допустим теперь, что пользователь открыл дверцу. Открыв ее он попал в состояние s1, где не один из AP не является истинным. Если он теперь закроет дверцу, он попадет обратно в s0. Если пользователь в состоянии s1 нажмет кнопку start, он попадет в состояние s2, в котором истинными являются предикаты er (error) и st (start).
В конце концов, рассуждая таким образом мы получим структуру Крипке, схематично изображенную на следующем слайде.
Слайд 29
Спецификация требований.
Примечание. Отбросив надписи на ребрах на
предыдущем слайде, получим структуру Крипке, соответствующую нашей системе.
Теперь
мы переходим ко второму этапу верификации, а именно к формализации требований.
При верификации методом Model Checking формальную спецификацию возможно задать формулой логики LTL, либо формулой CTL.
Стоит отметить, что реагирующие системы являются развивающимися во времени. Это и объясняет тот факт, что темпоральные логики идеально подходят для формализации свойств этих систем.
Примечание. Существует мнение, что сформулировать требования проще на языке LTL, а при использовании языка CTL мы имеем более простой алгоритм проверки на удовлетворение требований.
Слайд 30
Формализация требований.
Для формализации требований мы будем использовать логику
CTL.
Следует отметить, что CTL имеет несколько возможных базисов, но
наши требования мы можем формализовать используя всю мощь CTL, а затем свести полученные формулы требований к базису. (Базис нужен для упрощения алгоритма проверки).
Напомним, что нашим требованием было:
Ни при каких обстоятельствах не должно работать излучение СВЧ печи при открытой дверце. (Важность этого требования очевидна).
Очевидно это требование можно представить следующей формулой CTL:
AG(¬Cd ⇒ ¬Ht) – для любого пути (A) всегда справедливо (G), что из того, что дверца не закрыта следует то, что излучение выключено.
Слайд 31
Пример. Алгоритм MC для модели СВЧ печи
Выражая
наше требование через базис получим:
AG(¬Cd ⇒ ¬Ht) = ¬
EF¬ (¬Cd ⇒ ¬Ht) = ¬ E(True U ¬ (¬Cd ⇒ ¬Ht) )
Не существует такой ситуации, при которой сначала будет верно True, а затем встретится ситуация, когда не верно, что при открытой дверце не работает нагрев.
Теперь рассмотрим сам алгоритм. Его основная идея – для каждой подформулы (начиная с простых) заданной формулы CTL определить, в каких состояниях заданной структуры Крипке M эта подформула выполняется.
Этот алгоритм мы называли алгоритмом маркировки.
Слайд 32
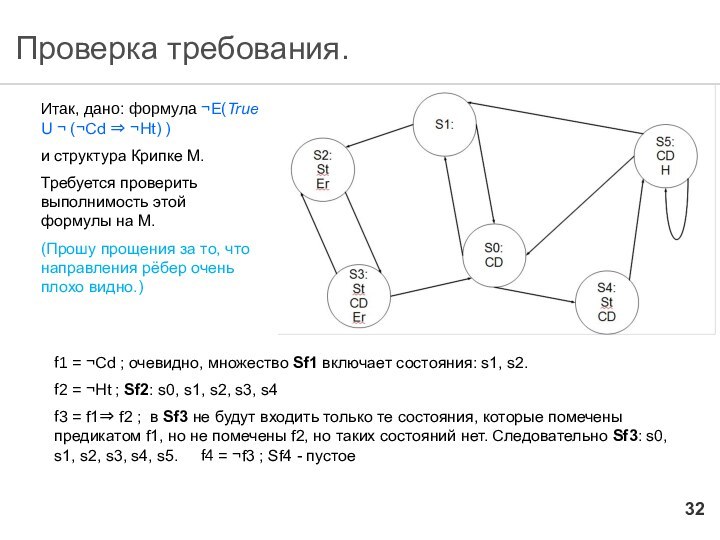
Проверка требования.
Итак, дано: формула ¬E(True U ¬ (¬Cd
⇒ ¬Ht) )
и структура Крипке M.
Требуется проверить выполнимость этой
формулы на M.
(Прошу прощения за то, что направления рёбер очень плохо видно.)
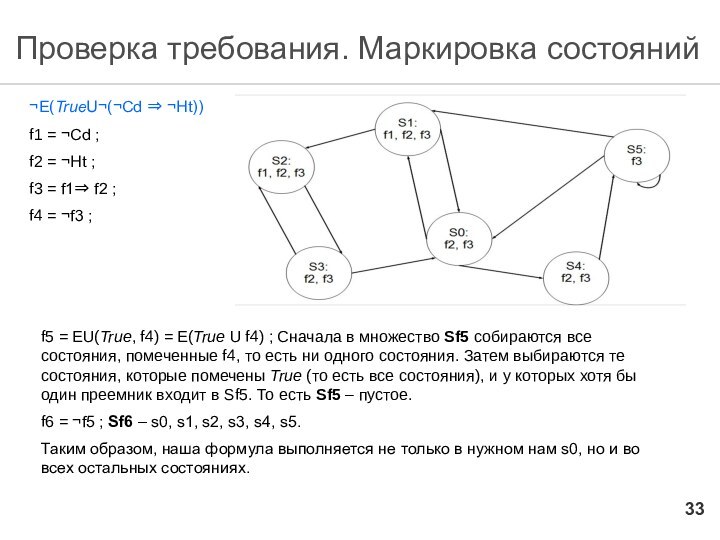
f1 = ¬Cd ; очевидно, множество Sf1 включает состояния: s1, s2.
f2 = ¬Ht ; Sf2: s0, s1, s2, s3, s4
f3 = f1⇒ f2 ; в Sf3 не будут входить только те состояния, которые помечены предикатом f1, но не помечены f2, но таких состояний нет. Следовательно Sf3: s0, s1, s2, s3, s4, s5. f4 = ¬f3 ; Sf4 - пустое
Слайд 33
Проверка требования. Маркировка состояний
f5 = EU(True, f4) =
E(True U f4) ; Сначала в множество Sf5 собираются
все состояния, помеченные f4, то есть ни одного состояния. Затем выбираются те состояния, которые помечены True (то есть все состояния), и у которых хотя бы один преемник входит в Sf5. То есть Sf5 – пустое.
f6 = ¬f5 ; Sf6 – s0, s1, s2, s3, s4, s5.
Таким образом, наша формула выполняется не только в нужном нам s0, но и во всех остальных состояниях.
¬E(TrueU¬(¬Cd ⇒ ¬Ht))
f1 = ¬Cd ;
f2 = ¬Ht ;
f3 = f1⇒ f2 ;
f4 = ¬f3 ;
Слайд 34
Верификация программ
Формальная верификация программ – это приемы и

методы формального доказательства (или опровержения) того, что модель программной
системы удовлетворяет заданной формальной спецификации.
На данный момент существует несколько методов реализации верификации программных систем. Самый распространенный из этих методов - Model Checking.
Стоит отметить что этот метод применяется в основном к реагирующим системам. Хотя его так же можно применить и к функциональным (трансформационным) системам.
Так же стоит отметить, что верификация предназначена прежде всего для систем, где очень важна надежность. То есть для таких систем, сбой в которых приводит к недопустимым последствиям. (Финансовые системы; системы жизнеобеспечения; бортовые системы машин, самолетов и других транспортных средств: медицинские и бытовые приборы etc.)
Давайте проведем сравнительный анализ верификации с еще одним распространенным методом проверки программ, а именно с тестированием. Рассмотрим преимущества и недостатки каждого из методов проверки.
Слайд 35
Тестирование. + и -
(+) Проверяется реальная программа, а
не ее модель.
(+) Проверка может быть выполнена в реальное
среде, с реальными интерфейсами.
(+) Проверять можно реальные наиболее опасные или часто используемые режимы работы системы.
( - ) Тестирование очень трудоемкий процесс.
( - ) Тестирование выполняется на поздних этапах разработки, поэтому цена исправления найденных ошибок очень велика.
( - ) Все реакции системы при выполнении тестирования должны быть заранее зафиксированы.
( - ) Тестированием можно проверить лишь немногие траектории вычисления системы, а их обычно бесконечное количество.
( - ) Тестирование сложных систем трудно автоматизируется.
( - ) Э. Дейкстра: “Тестированием можно доказать только наличие ошибок”, а не их отсутствие.
( - ) Тестированием плохо выявляются (точнее почти не выявляются) редко возникающие ошибки, особенно в параллельных системах и системах реального времени.
( - ) В случае выявлении ошибки, невозможно точно сказать, где она произошла.
Слайд 36
Верификация. + и -
(+) Происходит проверка всех возможных
вычислений модели системы на удовлетворение желаемого условия.
(+) Возможность автоматизировать
процесс.
(+) В случае нахождения ошибки указывается точная последовательность действий, которая к ней привела.
(+) Верификация возможна на любом из этапов разработки (включая начальный, когда нет реализации ни какой из компонент системы)
( - ) Язык спецификации требований системы может быть не полным, недостаточным для выражения желаемых свойств системы.
( - ) Сама автоматизированная система верификации может содержать ошибки.
( - ) Поскольку невозможно формально определить “полное отсутствие ошибок”, верификация (так же как и тестирование) не может гарантировать абсолютную правильность системы.
( - ) Не смотря на автоматизацию большей части верификации, приходится использовать высококвалифицированный персонал для составления адекватной модели системы.
Слайд 37
Вывод 1:
Верификация не является панацеей, это всего лишь
эффективный способ проверки. Действительно, вряд ли кто-то согласился бы
полететь на самолете, оборудованным бортовой системой, которая прошла верификацию, но никогда не тестировалась. Ни верификация, ни тестирование не могут по отдельности гарантировать необходимый уровень надежности системы. Эти методы нужно использовать вместе, так как их подходы взаимодополняющие.
Слайд 38
Свойства системы
Система
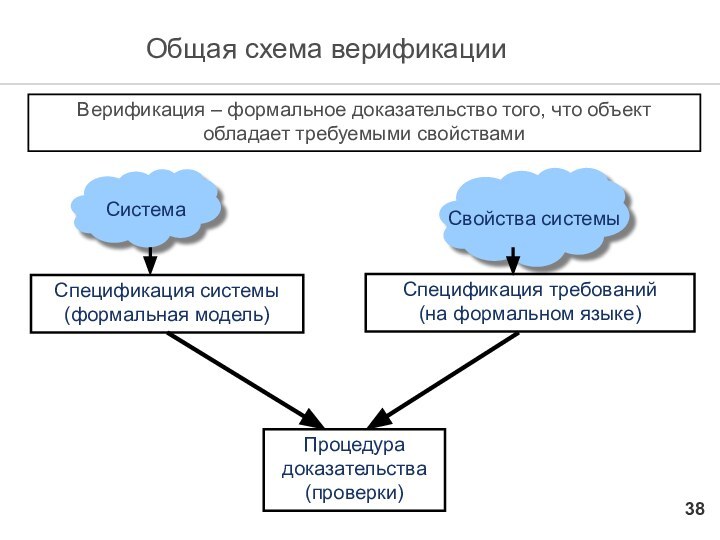
Общая схема верификации
Спецификация системы (формальная модель)
Процедура доказательства
(проверки)
Спецификация требований
(на формальном языке)
Верификация – формальное доказательство того,
что объект обладает требуемыми свойствами
Слайд 39
Этапы верификации
Согласно схеме, приведенной ранее, верификация состоит из
трех этапов:
1) Построение модели (возможно уже существующей системы), то
есть формализация системы. Это самый трудоёмкий процесс, требующий абстрагирования. Фактически, от того, на сколько хорошо будет построена модель, зависит вся дальнейшая кампания по верификации. Модель должна быть не слишком громоздкой, и при этом полностью отображать суть предметной области.
2) Составление, на одном из формальных языков требований системы.
3) Автоматизированная (ну или в нашем случае ручная) проверка на удовлетворение моделью требований к системе.
Примечание. Первый и второй этапы могут выполняться в любой последовательности.
Слайд 40
Итоги:
Я надеюсь, что не смотря на то, что
мы разобрали всего один простой пример, алгоритм верификации MC
стал достаточно ясным. Мы построили модель системы функционирования печи, специфицировали наши требования к ней, и доказали, используя алгоритм маркировки, что система отвечает им.
Так же хотелось бы сказать, что Model Checking имеет применение не только в реагирующих системах, но и в параллельных, где верификация особенно важна.
«Любая параллельная программа должна рассматриваться как неверная до тех пор, пока не доказано обратное.»
На следующих слайдах приведено несколько фактов о Model Checking.
Слайд 41
Примеры использования подхода
Cambridge ring protocol
IЕЕЕ Logical Link
Control protocol, LLC 802.2
фрагменты больших протоколов XTP и
TCP/IP
отказоустойчивые системы, протоколы доступа к шинам, протоколы контроля ошибок в аппаратуре,
криптографические протоколы
протокол Ethernet Сollision Avoidance
DeepSpace1 (NASA). Уже после тщательного тестирования и сдачи системы были найдены несколько критических ошибок
Верифицированные системы, в которых выявлены ошибки
Слайд 42
Model checking
Model checking - метод верификации ПО и
аппаратуры, основанный на изящных формальных методах. Это качественный прорыв
в верификации
ACM : Премия Тьюринга в июне 2008 г. была вручена трем создателям техники MODEL CHECKING, внесшим в нее наиболее существенный вклад:
Edmund Clarke (CMU)
Allen Emerson (CMU)
Joseph Sifakis (VERIMAG )
“за их роль в превращении метода Model checking в высокоэффективную технологию верификации, широко используемую в индустрии разработки программного обеспечения и аппаратных средств”
Stuart Feldman, Президент ACM:
“Это великий пример того, как технология, изменившая промышленность, родилась из чисто теоретических исследований”
Слайд 43
Литература
Ю.Г.Карпов. Model checking. Верификация параллельных и распределенных программных
систем.
// БХВ. Петербург, 2010
А.М.Миронов. Верификация программ
методом Model Сhecking.
// Издательство и год не указаны
Некоторые интернет ресурсы, в частности, wikipedia.
Слайд 44
Заключение
Model checking – достигшая зрелости область формального анализа,
интенсивно использующаяся для верификации дискретных систем
Model checking имеет множество
применений в разнообразных областях анализа динамических систем
Существует ряд проблем, препятствующих простому применению этого подхода в индустрии разработки ПО
В настоящее время - это область интенсивных исследований