Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Теоретические основы информатики

Содержание

MCMXCVIII=1000+(1000-100)+(100-10)+5+1+1+1=1998
Занятие в четверг у заочников ИФТИСпервая пара курсаТеоретические основы информатикиПредставление числа в MCMXCVIII=1000+(1000-100)+(100-10)+5+1+1+1=1998 Запись числа из n цифр в виде полинома в системе счисления с Перевод чисел из двоичной системы счисления в десятичную.Двоичное число записываем в полной Представим число 10000112 в десятичной системе счисления:Ответ: 10000112=671016050403021110 = 1∙20+1∙21+0∙22+0∙23+0∙24+0∙25+1∙26= 1+2+0+0+0+0+64= 6710 а0=1Свойство степени == Представим число 1038 в десятичной системе счисления:Ответ: 1038=6710120130= 3∙80+0∙81+1∙82=3+0+64=6710 Представим число 7В16 в десятичной системе счисления:Ответ: 7В16 = 12310 71В0 = 11∙160+7∙161=11+112=12310 1. Десятичное число делится нацело на 2, пока это возможно.2. На каждом 1. Десятичная дробь последовательно умножается Представим число 67,записанное в десятичной системе счисления в позиционных системах счисления: двоичной, Представим число 6710 в двоичной системе счисления:331168421Ответ: 6710 = 10000112 67Представим число 6710 в восьмеричной системе счисления:831Ответ: 6710 = 1038 Представим число 6710 в шестнадцатеричной с/с:674Ответ: 6710 = 4316 Правила перехода Из десятичной системы счисления в позиционные системы счисления:Разделить десятичное Представим число 12310 в шестнадцатеричной системе счисления:711ВОтвет: 12310 = 7В16 Перевод чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную и обратно».22.01.17 Перевод чисел с основанием 2nДвоичная система, являющаяся основой компьютерной арифметики, весьма громоздка Таблица натуральных чисел в четырех системах счисления10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 Тройка двоичных цифр - триадаЧетвёрка двоичных цифр - тетрада Правила10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 101011012 → 10  101 101 → 2558. Убедимся в правильности алгоритма:101011012 → 010 101 101 → 2558. Убедимся в правильности 101011012 → 010 101 101 → 2558. 0,100 11 2 → 0,100 110 2 → 0,4680,100 110→ 1*2-1+0*2-2+0*2-3+1*2-4+1*2-5+0*2-6 = 10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 3158 → 3 1 5 → 11 10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 Пример для 16-ой системы счисления Перевести в 8-ричную и 16-ричную системы счисления двоичное число 1010101,011112Перевести в 2-ичную (остаток от занятия) Дано двоичное число 1010101,011112Дано шестнадцатеричное число EF,1216Перевести эти
Слайды презентации

Слайд 2 MCMXCVIII=1000+(1000-100)+(100-10)+5+1+1+1=1998

MCMXCVIII=1000+(1000-100)+(100-10)+5+1+1+1=1998

Слайд 3 Запись числа из n цифр в виде полинома

Запись числа из n цифр в виде полинома в системе счисления

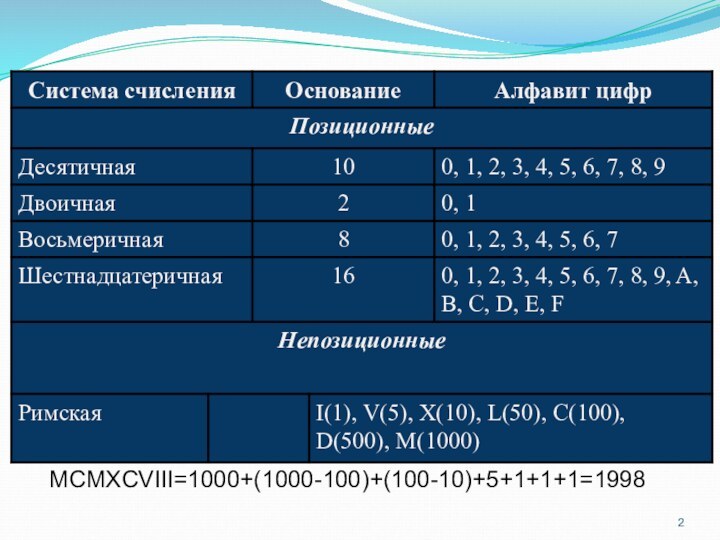
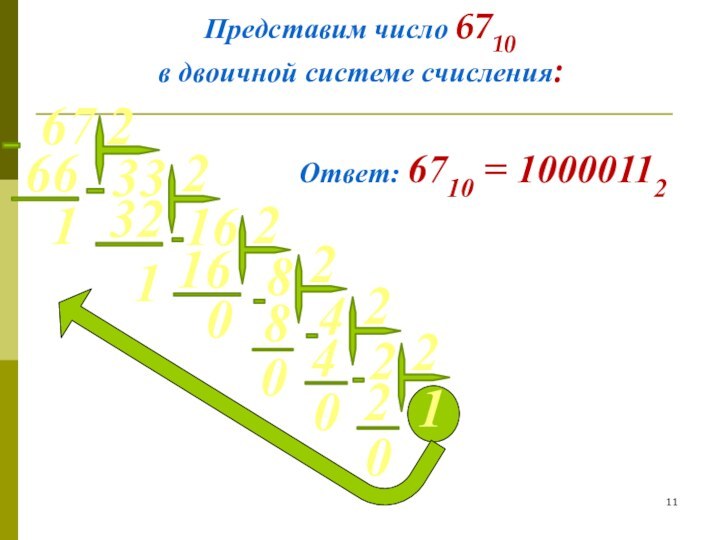
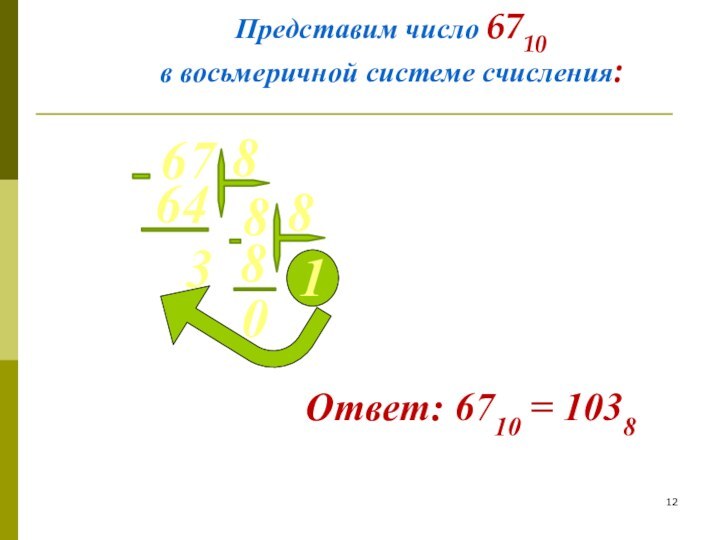
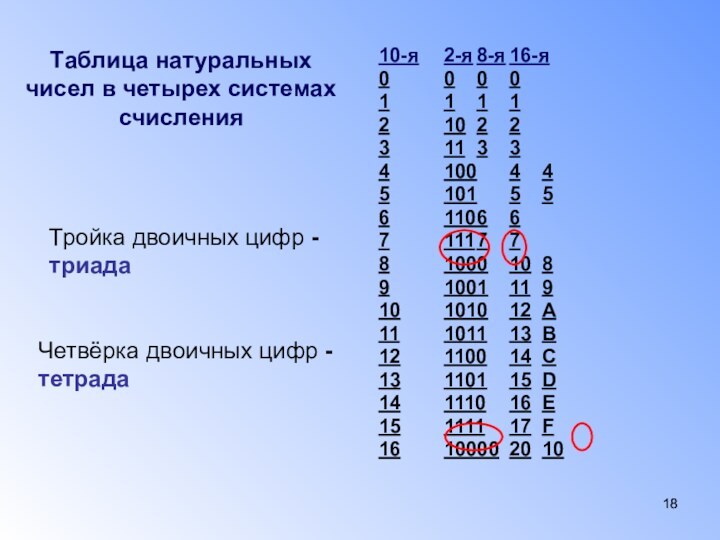
в системе счисления с основанием m
Десятичное число записываем в

полной форме:
640210= 6*103 + 4* 102+0* 101+2* 100 =
= 6000 + 400 + 0 + 2*1

xn-1xn-2xn-3…x1x0 =
= xn-1*mn-1 + xn-2*mn-2+ xn-3*mn-3+...+x1*m1 +x0*m0
mi-вес i – го знакоместа 0<= i <=(n-1)
Xi- символ в i – й позиции 0<=xi<=(m-1)



m=10 n=4

Слайд 4 Перевод чисел из двоичной системы счисления в десятичную.
Двоичное

Перевод чисел из двоичной системы счисления в десятичную.Двоичное число записываем в

число записываем в полной форме:

(1011)2 = 1*23 + 0*

22+1* 21+1* 20 =
= 8 + 0 + 2 + 1 = (11)10

Используем таблицу степеней двойки

Слайд 5 Представим число 10000112
в десятичной системе счисления:
Ответ: 10000112=6710
16050403021110

Представим число 10000112 в десятичной системе счисления:Ответ: 10000112=671016050403021110 = 1∙20+1∙21+0∙22+0∙23+0∙24+0∙25+1∙26= 1+2+0+0+0+0+64= 6710 а0=1Свойство степени ==

= 1∙20+1∙21+0∙22+0∙23+0∙24+0∙25+1∙26=
1+2+0+0+0+0+64= 6710
а0=1
Свойство степени
=
=

Слайд 6 Представим число 1038
в десятичной системе счисления:
Ответ: 1038=6710
120130=

Представим число 1038 в десятичной системе счисления:Ответ: 1038=6710120130= 3∙80+0∙81+1∙82=3+0+64=6710

3∙80+0∙81+1∙82=3+0+64=6710

Слайд 7 Представим число 7В16
в десятичной системе счисления:
Ответ: 7В16

Представим число 7В16 в десятичной системе счисления:Ответ: 7В16 = 12310 71В0 = 11∙160+7∙161=11+112=12310

= 12310
71В0 = 11∙160+7∙161=11+112=12310

Слайд 8 1. Десятичное число делится нацело на 2, пока

1. Десятичное число делится нацело на 2, пока это возможно.2. На

это возможно.
2. На каждом шаге записывается остаток от деления.


Перевод

чисел из десятичной системы счисления в двоичную.

6402:2= 3201+0 100:2=50+0
3201:2=1600+1 50:2=25+0
1600:2=800+0 25:2=12+1
800:2=400+0 12:2=6+0
400:2=200+0 6:2=3+0
200:2=100+0 3:2=1+1
1

3. Снизу вверх записываем цифры, начиная с последнего
частного и все остатки от деления.

640210=1 100 100 000 0102

Слайд 9 1. Десятичная дробь последовательно умножается

1. Десятичная дробь последовательно умножается

на основание системы счисления 2.
2. На каждом шаге записывается в результат полученная целая часть, которая в дальнейшем умно-жении не участвует.
3. Количество операций умножения зависит от требуемой точности вычислений.

Перевод дробных чисел
из 10-ой системы счисления в 2 с/c.

0,19*2 1,04*2
0,38*2 0,08*2
0,76*2 0,16*2
1,52*2 0,32

0,1910=0,001 100 02

Слайд 10 Представим число 67,записанное в десятичной системе счисления в

Представим число 67,записанное в десятичной системе счисления в позиционных системах счисления:

позиционных системах счисления: двоичной, восьмеричной, шестнадцатеричной.
6710 = А2
6710 =

А8

6710 = А16

Слайд 11
Представим число 6710
в двоичной системе счисления:
33
1
16
8
4
2
1
Ответ: 6710

Представим число 6710 в двоичной системе счисления:331168421Ответ: 6710 = 10000112

= 10000112

Слайд 12
67
Представим число 6710
в восьмеричной системе счисления:
8
3
1

Ответ: 6710

67Представим число 6710 в восьмеричной системе счисления:831Ответ: 6710 = 1038

= 1038

Слайд 13
Представим число 6710
в шестнадцатеричной с/с:
67
4

Ответ: 6710 =

Представим число 6710 в шестнадцатеричной с/с:674Ответ: 6710 = 4316

4316

Слайд 14 Правила перехода
Из десятичной системы счисления
в

Правила перехода Из десятичной системы счисления в позиционные системы счисления:Разделить десятичное

позиционные системы счисления:
Разделить десятичное число на основание системы счисления.

Получится частное и остаток.

Выполнять деление до тех пор, пока последнее частное не станет меньшим основания новой системы счисления.

Записать последнее частное и все остатки в обратном порядке. Полученное число и будет записью в новой системы счисления.

Слайд 15

Представим число 12310
в шестнадцатеричной системе счисления:
7
11

В

Ответ: 12310

Представим число 12310 в шестнадцатеричной системе счисления:711ВОтвет: 12310 = 7В16

= 7В16

Слайд 16 Перевод чисел
из двоичной системы счисления
в восьмеричную,

Перевод чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную и обратно».22.01.17

шестнадцатеричную и обратно».
22.01.17

Слайд 17
Перевод чисел с основанием 2n
Двоичная система, являющаяся основой

Перевод чисел с основанием 2nДвоичная система, являющаяся основой компьютерной арифметики, весьма

компьютерной арифметики, весьма громоздка и неудобна для использования человеком.


Поэтому программисты используют две кратные двоичной системы счисления: восьмеричную и шестнадцатеричную.
8=23 16=24

Слайд 18
Таблица натуральных чисел в четырех системах счисления
10-я 2-я 8-я 16-я
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 А
11 1011 13 В
12 1100 14 С
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10





Тройка двоичных

Таблица натуральных чисел в четырех системах счисления10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 Тройка двоичных цифр - триадаЧетвёрка двоичных цифр - тетрада

цифр - триада
Четвёрка двоичных цифр - тетрада

Слайд 19 Правила
10-я 2-я 8-я 16-я
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 А
11 1011 13 В
12 1100 14 С
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10



101011012 → 10  101 101 → 2558.

Правила10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 101011012 → 10  101 101 → 2558. 2


2 5

5

Деление на группы в целой части идёт справа налево

Для перевода дробной части число читается слева направо.

0,100 110 2 → 0,468



0,1910 = 0,001 100 02 → 0,148

Слайд 20 Убедимся в правильности алгоритма:
101011012 → 010 101 101 →

Убедимся в правильности алгоритма:101011012 → 010 101 101 → 2558. 2

2558.
2 5

5
101011012 = 1*27+1*25+1*23+1*22+1*20 =1*128+1*32+1*8+1*4+1*1= 128+32+8+4+1= 17310
2558 = 2*82+5*81+5*80 = 2*64+5*8+5*1= =128+40+5 = 17310.

Слайд 21 Убедимся в правильности
101011012 → 010 101 101 →

Убедимся в правильности 101011012 → 010 101 101 → 2558.

2558.
2 5

5

2558 = 2*82+5*81+5*80 = 2*64+5*8+5*1= =128+40+5 = 17310.

Слайд 22 0,100 11 2 → 0,100 110 2 →

0,100 11 2 → 0,100 110 2 → 0,4680,100 110→ 1*2-1+0*2-2+0*2-3+1*2-4+1*2-5+0*2-6

0,468
0,100 110→ 1*2-1+0*2-2+0*2-3+1*2-4+1*2-5+0*2-6 =
= 1*0,5+1*0,0625+1*0,031=0,59410
0,468 → 4*8-1+6*8-2 →

4*0,125+6*0,0156 =0,59410

Если в триаде или тетраде не хватает цифр, то дописывают нули справа.

Для дробной части

Слайд 23 10-я 2-я 8-я 16-я
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 А
11 1011 13 В
12 1100 14 С
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10






3158 → 3 1

10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 3158 → 3 1 5 → 11 001 1012

5 → 11 001 1012

011 001  101

Если в триаде или тетраде не хватает цифр, то дописывают нули слева.






Правила

Слайд 24 10-я 2-я 8-я 16-я
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 А
11 1011 13 В
12 1100 14 С
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10

Пример для 16-ой системы счисления

10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 А 11 1011 13 В 12 1100 14 С 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 Пример для 16-ой системы счисления

Слайд 25

Перевести в 8-ричную и 16-ричную системы счисления двоичное

Перевести в 8-ричную и 16-ричную системы счисления двоичное число 1010101,011112Перевести в

число 1010101,011112
Перевести в 2-ичную систему счисления число EF,1216
Перевести эти

2 числа в 10-ную с/с


Задание в аудитории:

  • Имя файла: teoreticheskie-osnovy-informatiki.pptx
  • Количество просмотров: 108
  • Количество скачиваний: 0
- Предыдущая Сложности и возможности развития кластеров в ИКТ сфере – примеры норвежских ИКТкластеров
Следующая - Экономические кризисы: причины, последствия, основные антикризисные меры

Похожие презентации

Число Пи и способы его вычисления на компьютере Число Пи и способы его вычисления на компьютере 139
Презентация День Победы презентация к уроку по информатике (подготовительная группа) Презентация День Победы презентация к уроку по информатике (подготовительная группа) 147
Безопасность web-приложений Безопасность web-приложений 219
Adobe Photoshop Adobe Photoshop 226
Файловые архивы Файловые архивы 143
История развития вычислительной техники История развития вычислительной техники 115
Внешняя память Средства хранения информации Внешняя память Средства хранения информации 140
iSpring Suite iSpring Suite 127
Графические операторы языка QBasic Графические операторы языка QBasic 138
Графическое представление информации Графическое представление информации 108
Программное обеспечение дистанционного образования Программное обеспечение дистанционного образования 113
Кодирование и обработка звуковой информации Кодирование и обработка звуковой информации 128
Презентация по теме Фильм и звук в презентации консультация по информатике по теме Презентация по теме Фильм и звук в презентации консультация по информатике по теме 137
ФУНКЦИИ ВВОДА И ВЫВОДА ФУНКЦИИ ВВОДА И ВЫВОДА 129
Минусы интернета Минусы интернета 141
Компьютерные вирусы. Антивирусные программы Компьютерные вирусы. Антивирусные программы 145
Чтение статей в EBSCOhost. Практическое занятие Чтение статей в EBSCOhost. Практическое занятие 104
Алфавит языка QBASIC Алфавит языка QBASIC 107
блок-схемы алгоритмов блок-схемы алгоритмов 110
Варианты создания UI в Android Варианты создания UI в Android 149
Ветвления и исполнители алгоритмов Ветвления и исполнители алгоритмов 123
Открыты урок по информатики Электрондык пошта (1 курс) Открыты урок по информатики Электрондык пошта (1 курс) 151
Компьютер и дети Компьютер и дети 90
Кодирование вещественных чисел Кодирование вещественных чисел 127
MSC.Dytran - 17 MSC.Dytran - 17 132
презентация по информатике презентация по информатике 126
Презентация по информатике Знакомство с клавиатурой Презентация по информатике Знакомство с клавиатурой 141
Экспертная система Wi-FIT PROJECT Экспертная система Wi-FIT PROJECT 122
Информация и ее свойства (7 класс) Информация и ее свойства (7 класс) 194
Презентация по информатике на тему Кодирование информации (5 класс) Презентация по информатике на тему Кодирование информации (5 класс) 119