Слайд 2
Коды
Определим код как представление множества символов строками, состоящими
из единиц и нулей.
Это множество символов обычно включает буквы
алфавита, цифры и, как правило, определенные контрольные символы.
Коды представляются бинарными строками с целью использования их компьютерами для хранения и передачи данных.
Слайд 3
Коды
Желательно, чтобы коды обладали некоторыми свойствами.
Наиболее важное
свойство кода состоит в том, что когда сообщение кодируется
как двоичная строка, состоящая из конкатенации элементов кода, эта конкатенация однозначна.
При декодировании сообщения не должно возникать проблем с тем, какую букву представляет элемент кода. Такой код назовем однозначно декодируемым кодом.
Слайд 4
Коды
Существует несколько способов достижения этой цели.
Один из
них – кодирование всех символов двоичными строками одной длины.
Такой код называется блоковым.
Например, если для кодирования каждого символа используется 8 бит, то известно, что каждые восемь бит представляют один символ передаваемого сообщения.
Блоковый код особенно полезен при ограничении длины кода для каждого посланного символа или буквы.
Слайд 7
Коды
Часто необходимо сжимать данные, чтобы минимизировать объем памяти
для их хранения или время для передачи данных.
Что
касается минимизации объема памяти, то наиболее эффективным является код Хаффмана. Преимущество кода Хаффмана состоит также в том, что это мгновенный код.
Хорошо известным примером кода, минимизирующего время передачи, является код Морзе.
Слайд 8
Коды
В кодах Хаффмана и Морзе буквы или символы,
которые встречаются наиболее часто, имеют более короткий код.
Слайд 9
Коды
В коде Морзе буквы разделены "пробелами", а слова
– тремя "пробелами". В данном случае "пробелы" – это
единицы времени.
Слайд 10
Коды
В процессе передачи данных могут возникать ошибки.
Все,
что может стать причиной ошибок, называется неопределенным термином "шум".
Например, данные, полученные от отдаленного космического корабля, наверняка подвержены различного рода шумам.
Слайд 11
Коды
В некоторых случаях интерес представляет только определение наличия
ошибки, что соответствует ситуации передачи данных еще раз.
Коды,
обладающие свойством определения наличия ошибок, называются кодами, обнаруживающими ошибки.
Слайд 12
Коды
В другом случае, когда данные не могут быть
переданы еще раз (например, данные от удаленного космического корабля),
требуется дополнительная информация о данных с целью не только обнаружения, но и исправления ошибки.
Коды, позволяющие исправлять ошибки, называются кодами, исправляющими ошибки.
Слайд 13
Коды
Может показаться разумным всегда использовать коды с исправлением
ошибок.
Проблема использования кодов с исправлением ошибок и кодов
с обнаружением ошибок состоит в том, что они должны включать в себя дополнительную информацию, поэтому они являются менее эффективными в отношении минимизации объема памяти.
Слайд 14
Коды
К сожалению, использование кодов с исправлением ошибок и
кодов с обнаружением ошибок не дает абсолютной гарантии того,
что ошибка будет исправлена или обнаружена.
Слайд 15
Коды
В качестве первого метода обнаружения ошибок рассмотрим бит
контроля четности.
Продемонстрируем этот метод на примере кода ASCII.
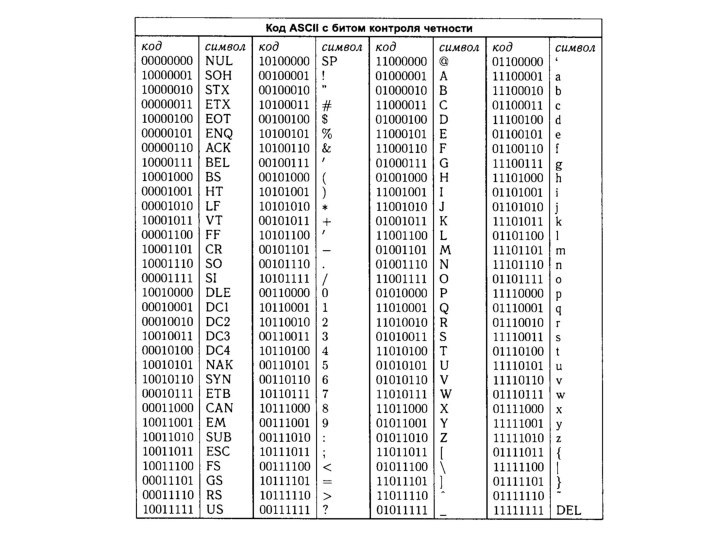
Слайд 16
Коды
ASCII-код является блоковым кодом, который использует 7 битов,
поэтому любой закодированный символ изображается строкой из семи символов
1 и 0.
Восьмой бит добавляется таким образом, чтобы количество единиц было четным.
Поэтому, если код переданной строки получен с единственной ошибкой, то количество единиц будет нечетным, и получатель информации поймет, что произошла ошибка.
Слайд 17
Коды
К сожалению, если произошло две ошибки, их нельзя
будет обнаружить, поскольку количество единиц опять будет четным.
Слайд 20
Коды
Если при кодировании каждая строка повторена один раз,
то в результате получаем код с обнаружением ошибок.
Если
произошла ошибка, то соответствующие позиции не будут совпадать.
Слайд 21
Коды
Например, если закодированная строка имеет вид 111111010110111011, то
ошибки имеются в третьем и в последнем битах.
Исправить
ошибки мы не можем, поскольку не знаем, в какой из копий какая ошибка присутствует.
Если кодируемая строка повторяется дважды, то лучше всего выявить ошибку.
Если имеются три копии строки, то можно исправить код при наличии единственной ошибки.
Слайд 22
Коды
Если имеется отличие в битах в соответствующих позициях
строк, то выбирается значение, которое встречается дважды.
Например, если
строка имеет длину 4 и нам передано 110110011101, то во второй позиции мы два раза получим 1 и один раз 0.
Таким образом, предполагаем, что правильное значение равно 1, и правильным вариантом закодированной строки является 1101.
Слайд 59
Декодирование по лидеру смежного класса
Слайд 60
Декодирование по лидеру смежного класса
Слайд 61
Декодирование по лидеру смежного класса
Слайд 62
Декодирование по лидеру смежного класса
Слайд 63
Декодирование по лидеру смежного класса
Слайд 64
Декодирование по лидеру смежного класса
Слайд 65
Декодирование по лидеру смежного класса
Слайд 66
Декодирование по лидеру смежного класса
Слайд 68
Декодирование по лидеру смежного класса
Слайд 69
Декодирование по лидеру смежного класса
Слайд 70
Декодирование по лидеру смежного класса
Слайд 71
Декодирование по лидеру смежного класса
Слайд 72
Декодирование по лидеру смежного класса
Слайд 75
Декодирование по лидеру смежного класса
Слайд 76
Декодирование по лидеру смежного класса
Слайд 77
Декодирование по лидеру смежного класса
Слайд 78
Декодирование по лидеру смежного класса
Слайд 80
Декодирование по лидеру смежного класса
Слайд 81
Декодирование по лидеру смежного класса
Слайд 83
Декодирование по лидеру смежного класса
Слайд 84
Декодирование по лидеру смежного класса
Слайд 85
Декодирование по лидеру смежного класса
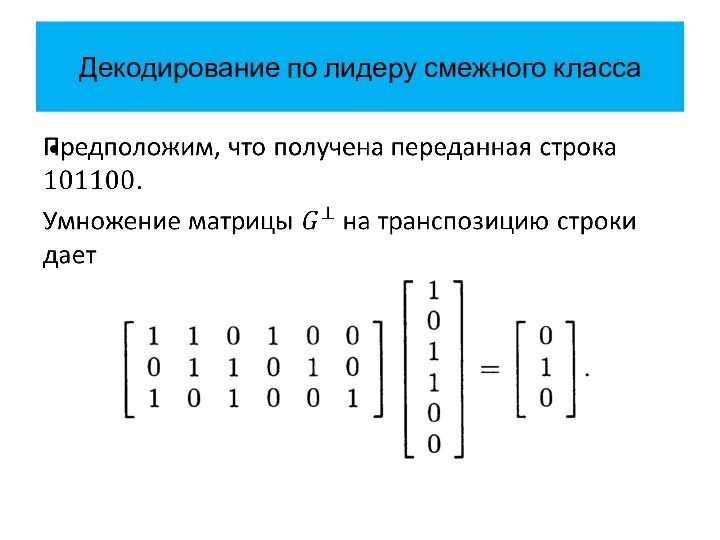
Снова вернемся к примеру:
,
.
Слайд 86
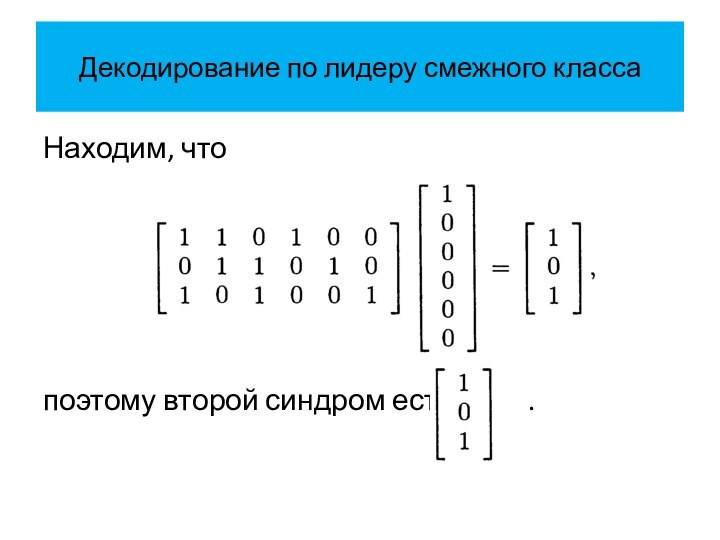
Декодирование по лидеру смежного класса
Уже известно, что первый
синдром есть
.
Слайд 87
Декодирование по лидеру смежного класса
Слайд 88
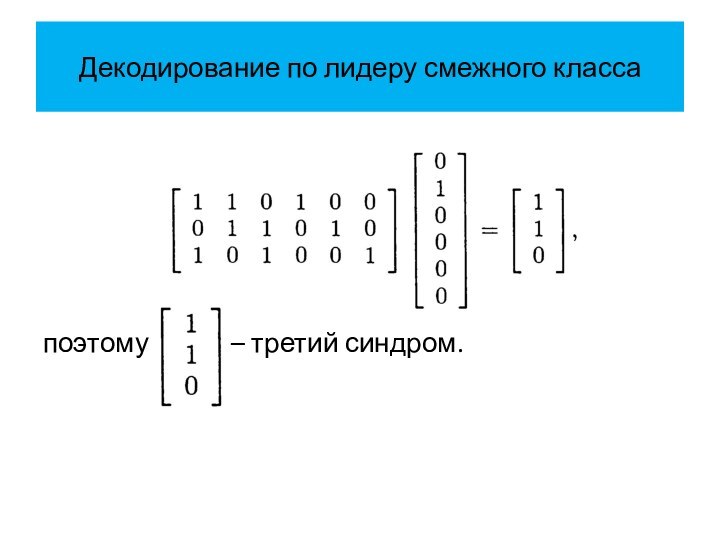
Декодирование по лидеру смежного класса
Находим, что
поэтому второй синдром
есть .
Слайд 89
Декодирование по лидеру смежного класса
Слайд 90
Декодирование по лидеру смежного класса
поэтому
– третий синдром.
Слайд 91
Декодирование по лидеру смежного класса
Слайд 92
Декодирование по лидеру смежного класса
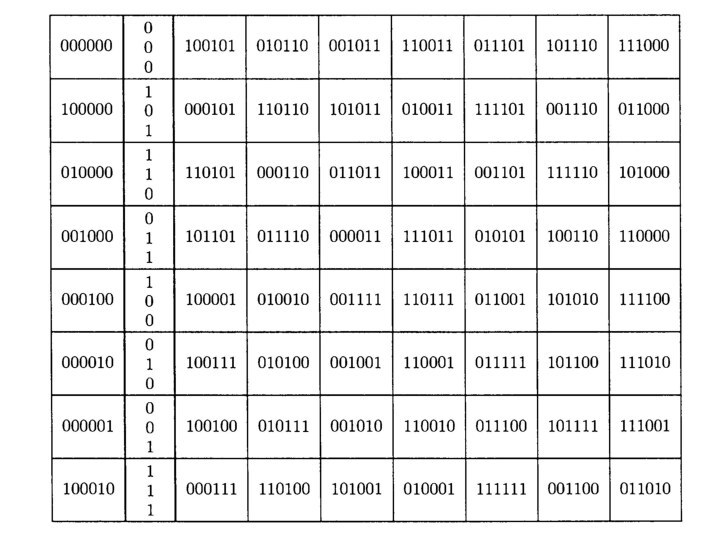
Продолжая процесс, получаем следующую
таблицу.
Слайд 94
Декодирование по лидеру смежного класса
Слайд 95
Декодирование по лидеру смежного класса
Слайд 96
Декодирование по лидеру смежного класса
Слайд 97
Декодирование по лидеру смежного класса
Заметим, однако, что процесс
можно сделать еще быстрее.
При этом потребуются только два
первых столбца приведенной выше таблицы.
Слайд 98
Декодирование по лидеру смежного класса
Слайд 99
Декодирование по лидеру смежного класса
Слайд 100
Декодирование по лидеру смежного класса
Слайд 101
Декодирование по лидеру смежного класса
Слайд 102
Декодирование по лидеру смежного класса
Слайд 103
Декодирование по лидеру смежного класса
Слайд 104
Коды Хемминга
В рассматриваемом примере существуют определенные трудности при
попытке исправить код для некоторых строк, поскольку все лидеры
имеют вес 1.
Эти трудности устраняются путем использования матрицы, называемой матрицей Хемминга, в качестве порождающей матрицы.
Слайд 108
Коды Хемминга
Для изучения матриц Хемминга необходимо понятие расстояния
и его связь с весом каждой из строк.
Начнем
с теоремы о весах строк.
Слайд 116
Коды Хемминга
В приведенной далее теореме сформулирован важный критерий
для определения числа ошибок, которые могут быть исправлены или
обнаружены с использованием кода.