Слайд 3
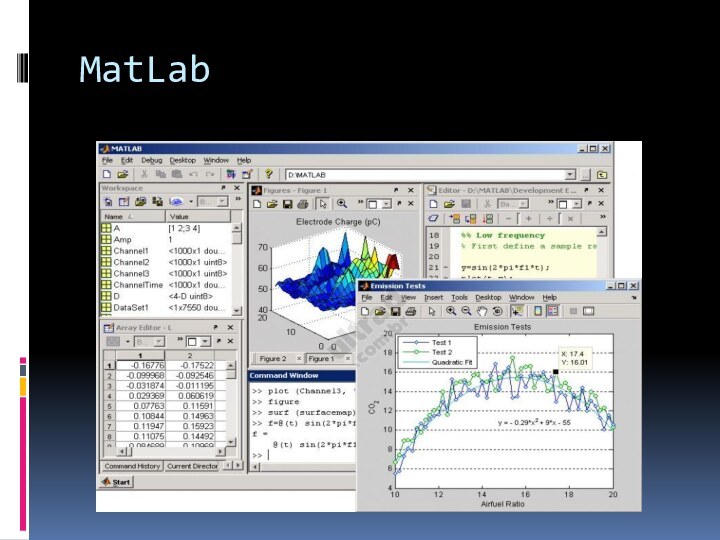
MatLab — одна из тщательно проработанных и
проверенных временем систем автоматизации математических расчетов, построенная на расширенном
представлении и применении МАТРИЧНЫХ операций.
Библиотека C Math позволяет пользоваться следующими категориями функций:
Слайд 4
Библиотека C Math позволяет пользоваться следующими категориями функций:
операции
с матрицами;.
сравнение матриц;
решение линейных уравнений;
разложение операторов и поиск собственных
значений;
нахождение обратной матрицы;
поиск определителя;
вычисление матричного экспоненциала;
элементарная математика;
функции beta, gamma, erf и эллиптические функции;
основы статистики и анализа данных;
поиск корней полиномов;
фильтрация, свертка;
быстрое преобразование Фурье (FFT);
интерполяция;
операции со строками;
операции ввода-вывода файлов и т.д.
Слайд 5
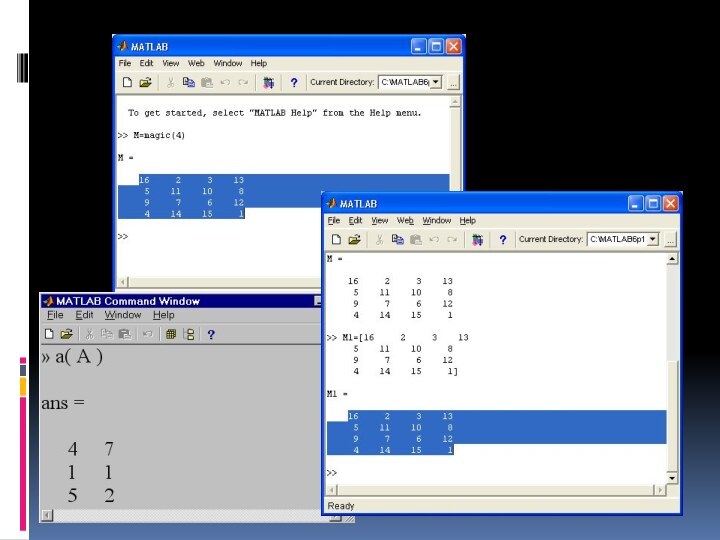
Матрицы MATLAB
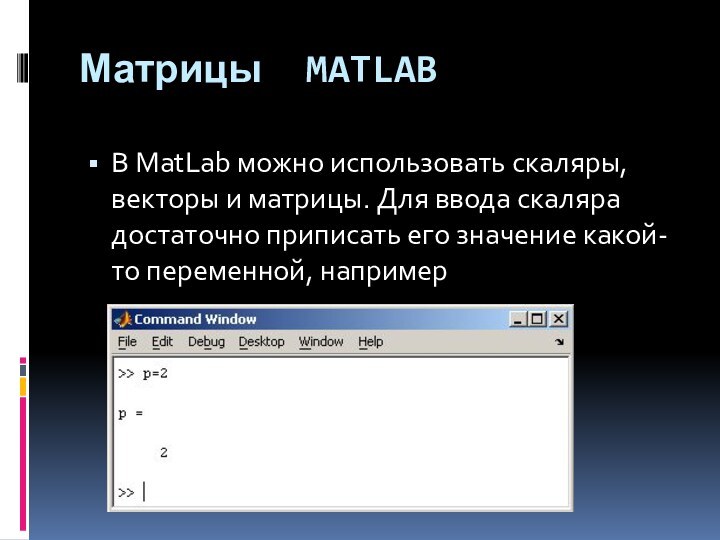
В MatLab можно использовать скаляры, векторы и
матрицы. Для ввода скаляра достаточно приписать его значение какой-то
переменной, например
Слайд 6
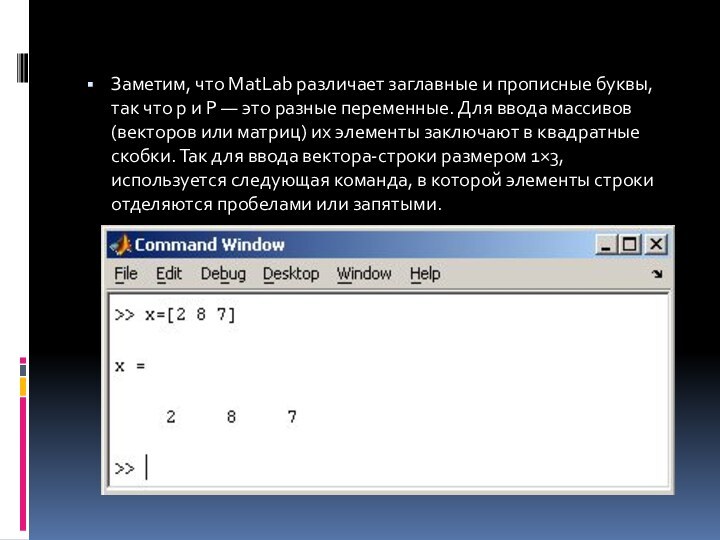
Заметим, что MatLab различает заглавные и прописные буквы,
так что p и P — это разные переменные. Для ввода массивов (векторов
или матриц) их элементы заключают в квадратные скобки. Так для ввода вектора-строки размером 1×3, используется следующая команда, в которой элементы строки отделяются пробелами или запятыми.
Слайд 7
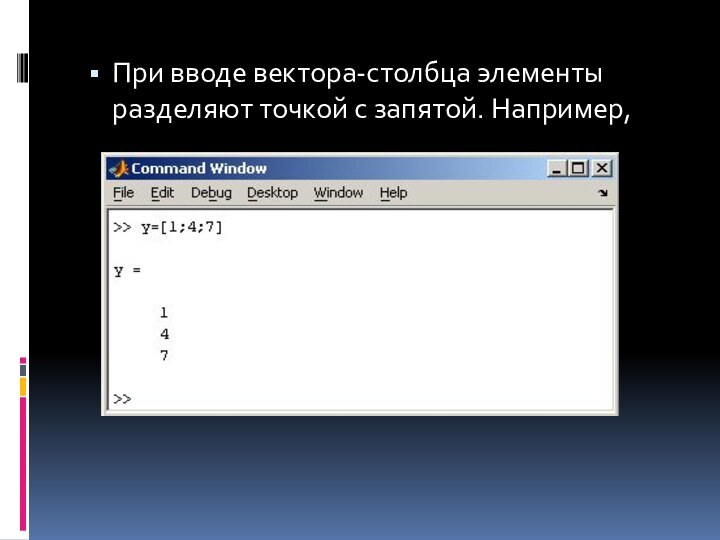
При вводе вектора-столбца элементы разделяют точкой с запятой.
Например,
Слайд 8
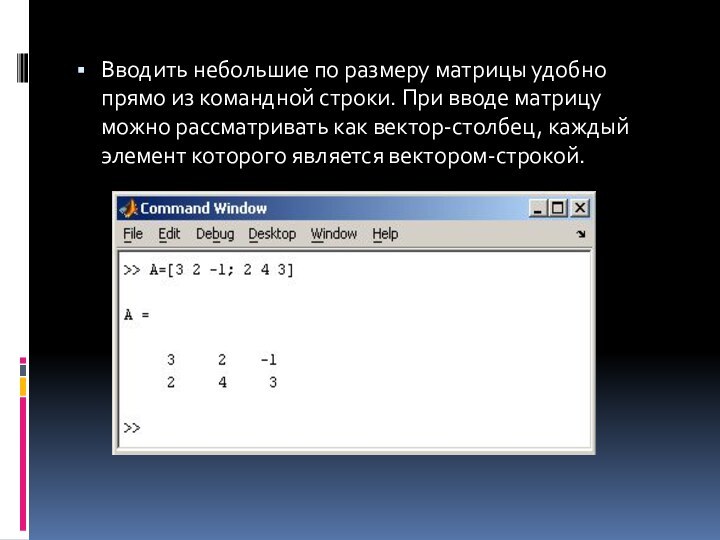
Вводить небольшие по размеру матрицы удобно прямо из
командной строки. При вводе матрицу можно рассматривать как вектор-столбец,
каждый элемент которого является вектором-строкой.
Слайд 9
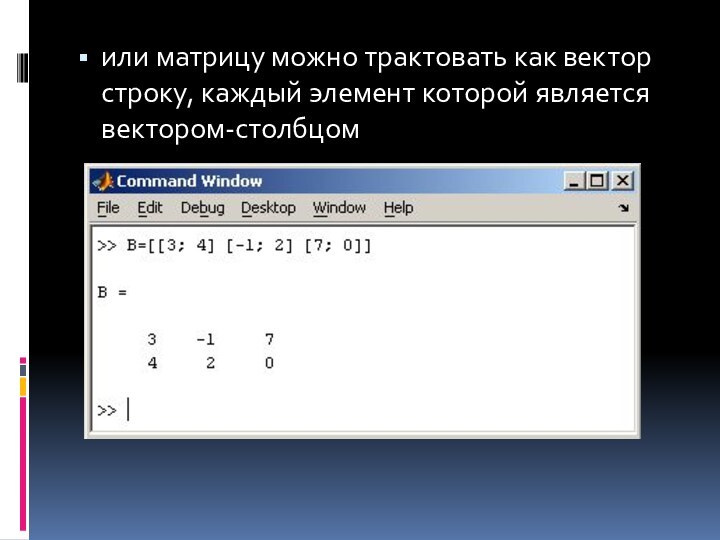
или матрицу можно трактовать как вектор строку, каждый
элемент которой является вектором-столбцом
Слайд 10
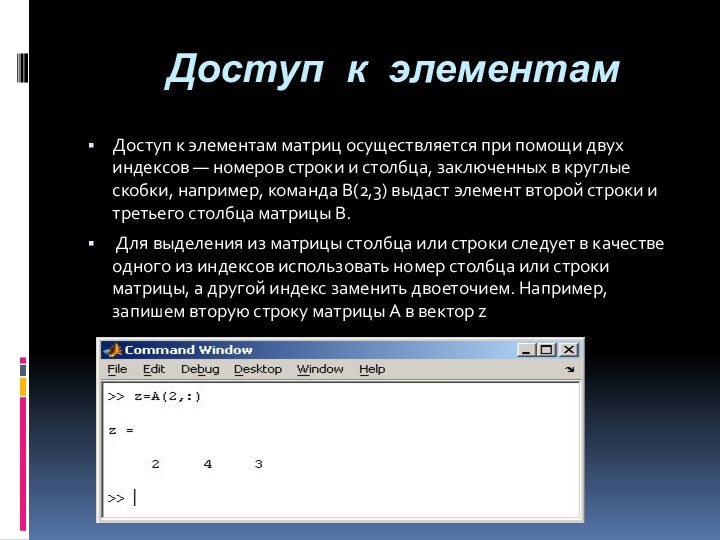
Доступ к элементам
Доступ к элементам матриц
осуществляется при помощи двух индексов — номеров строки и
столбца, заключенных в круглые скобки, например, команда B(2,3) выдаст элемент второй строки и третьего столбца матрицы B.
Для выделения из матрицы столбца или строки следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить двоеточием. Например, запишем вторую строку матрицы A в вектор z
Слайд 11
Также можно осуществлять выделение блоков матриц при помощи
двоеточия. Например, выделим из матрицы P блок отмеченный цветом
Слайд 12
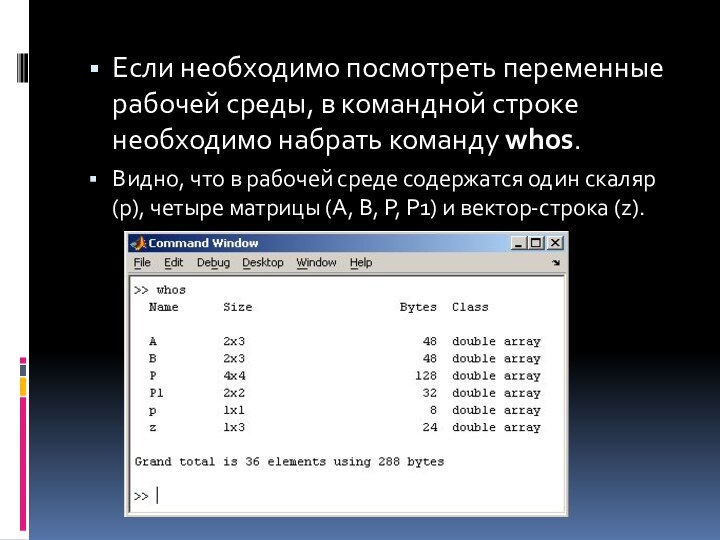
Если необходимо посмотреть переменные рабочей среды, в командной
строке необходимо набрать команду whos.
Видно, что в рабочей среде содержатся
один скаляр (p), четыре матрицы (A, B, P, P1) и вектор-строка (z).
Слайд 13
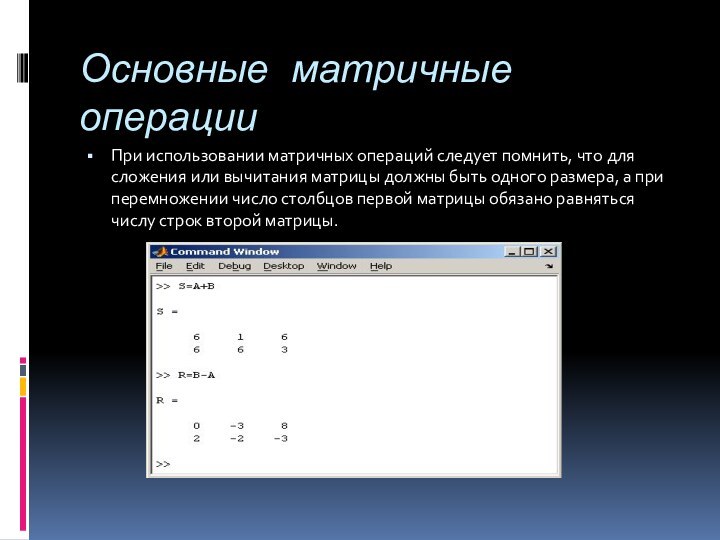
Основные матричные операции
При использовании матричных операций следует помнить,
что для сложения или вычитания матрицы должны быть одного
размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы.
Слайд 14
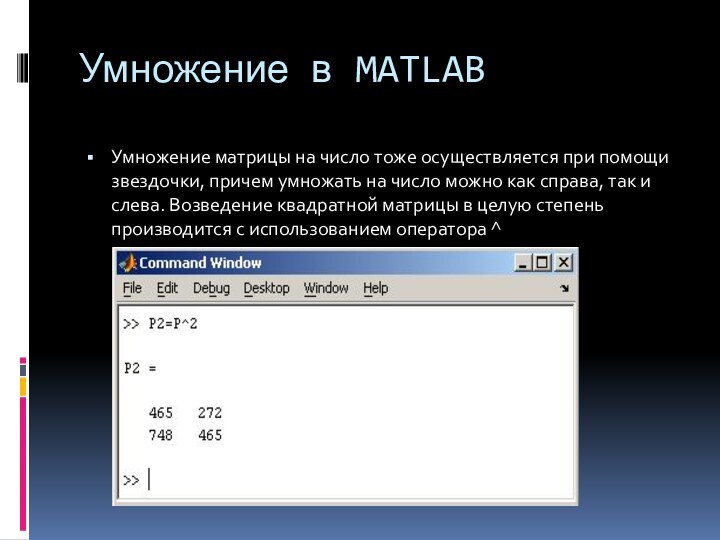
Умножение в MATLAB
Умножение матрицы на число тоже осуществляется
при помощи звездочки, причем умножать на число можно как
справа, так и слева. Возведение квадратной матрицы в целую степень производится с использованием оператора ^
Слайд 15
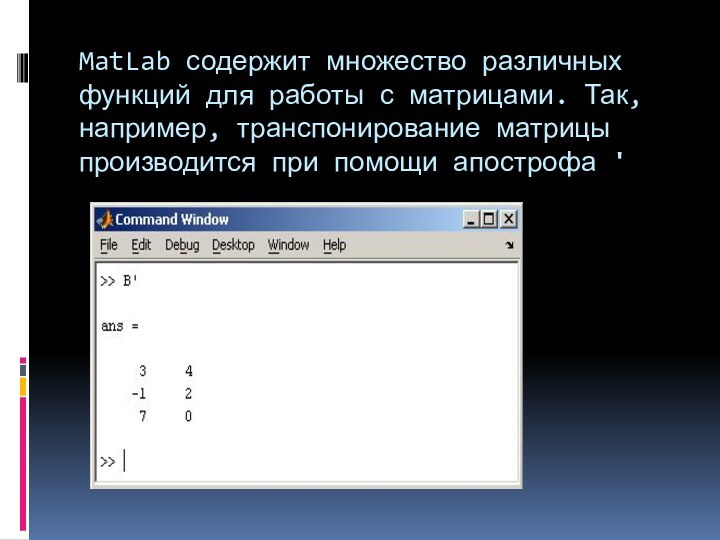
MatLab содержит множество различных функций для работы с
матрицами. Так, например, транспонирование матрицы производится при помощи апострофа '
Слайд 16
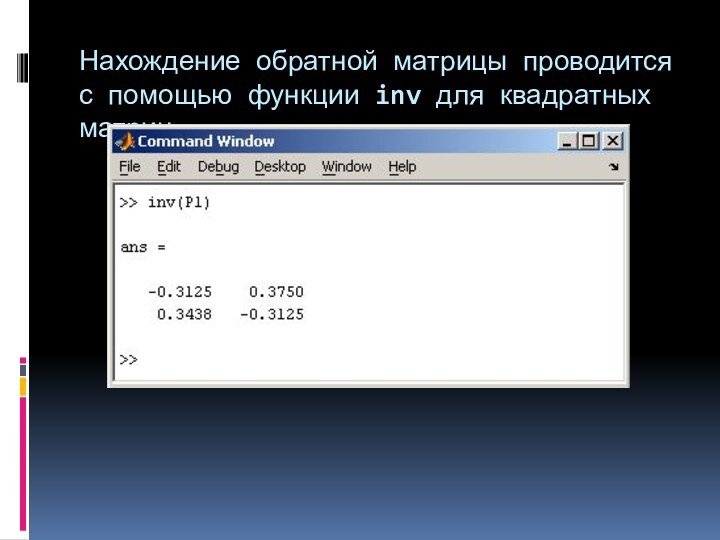
Нахождение обратной матрицы проводится с помощью функции inv для квадратных
матриц
Слайд 19
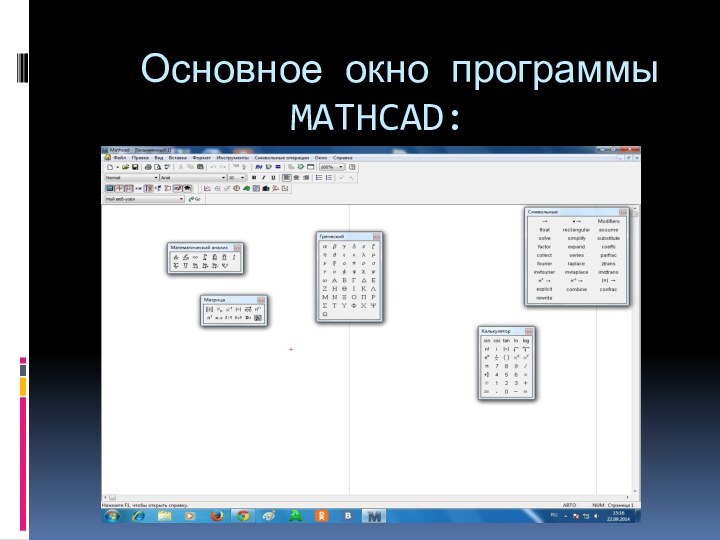
Основное окно программы MATHCAD:
Слайд 20
ДЕЙСТВИЯ НАД МАТРИЦАМИ В МАТКАД.
Панель матриц
Слайд 21
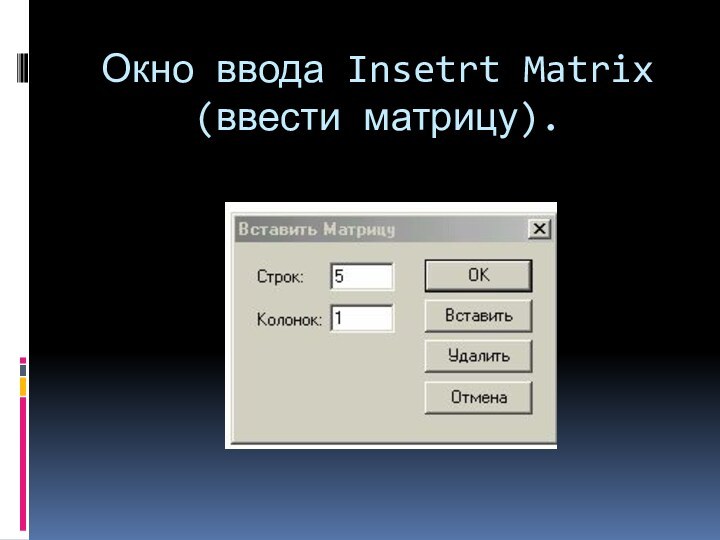
Окно ввода Insetrt Matrix (ввести матрицу).
Слайд 23
Над векторами определены показанные на рисунке
операции сложения и вычитания, транспонирования, умножения по математическим правилам
умножения матриц. Знак транспонирования следует вводить с панели Matrix (матрица).
Порядковый номер элемента, который является его адресом, называется индексом.
Нижняя граница индексации задается значением системной переменной ORIGIN, которая может принимать значение 0 или 1.
Слайд 24
Задача 1. Ввести все векторы рис.5 и произвести
над ними все действия, проведенные на рисунке.
Матрицы в
Маткаде вводятся так же, как и векторы, но число столбцов в них больше единицы. Элементами матрицы могут быть также числа, буквы, выражения. Как и в случае векторов, буквенные элементы и элементы – выражения должны быть предварительно определены численно. На рисунке показаны различные способы ввода матриц.
Слайд 25
Команды панели Matrix:
кнопка индексации элементов матрицы,
кнопка обращения матрицы,
кнопка скалярного произведения векторов и матриц
кнопка транспонирования матрицы,
кнопка векторного произведения двух векторов
кнопка сложения векторов
кнопка выделения столбца матрицы
кнопка вычисления детерминанта матрицы.
Слайд 27
Определение матрицы:
matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…,[an1,an2,…,anm]]),
где n −
число строк, m – число столбцов в матрице.
Слайд 28
Например:
> A:=matrix([[1,2,3],[-3,-2,-1]]);
A:= 1 2
3
-3 -2 -1
Слайд 29
Диагональная матрица:
> J:=diag(1,2,3);
1 0 0
J:=
0 2 0
0 3 0
Слайд 30
Генерировать матрицу можно с помощью функции f(i, j)
от
переменных i, j – индексов матрицы: matrix(n, m, f),
где где n -
число строк, m – число столбцов.
A:=matrix(2,3,f);
xy xy^2 xy
A:= x^2y x^2y^2 x^2y^3
Число строк в матрице А можно определить с помощью команды
rowdim(A), а число столбцов – с помощью команды coldim(A).
Слайд 31
Арифметические операции с матрицами.
Сложение двух матриц одинаковой размерности
осуществляется
теми же командами, что и сложение векторов: evalm(A+B) или
matadd(A,B). Произведение двух матриц может быть найдено с помощью двух команд:
1) evalm(A&*B);
2) multiply(A,B).
Слайд 32
В качестве второго аргумента в командах, вычисляющих произведение,
можно указывать вектор, например:
> A:=matrix([[1,0],[0,-1]]);
> B:=matrix([[-5,1], [7,4]]);
B:=
-5 1
0 -1 7 4
>v:=vector([2,4]);
>v := [2,4]
multiply(A,v);
[2,−4]











![Задачи символьной алгебры в пакетах символьной математики Определение матрицы:matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…,[an1,an2,…,anm]]), где n − число строк, m – число столбцов в матрице.](/img/tmb/12/1121983/9504a71687e2e783b613164a016c81c2-720x.jpg)
![Задачи символьной алгебры в пакетах символьной математики Например:> A:=matrix([[1,2,3],[-3,-2,-1]]);A:= 1 2 3](/img/tmb/12/1121983/796c52f270687cbbb857f0a63e7ce314-720x.jpg)



![Задачи символьной алгебры в пакетах символьной математики В качестве второго аргумента в командах, вычисляющих произведение, можно указывать вектор, например:> A:=matrix([[1,0],[0,-1]]);> B:=matrix([[-5,1], [7,4]]);](/img/tmb/12/1121983/c01b40090af79430af29cd50d5517e81-720x.jpg)

