- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к проекту по математике Числа - ГИГАНТЫ (5 класс)
Содержание
- 2. «В сочетании цифр есть безусловная магия,
- 3. Актуальность: в школьном курсе «математика» не изучается
- 4. Объект исследования: удивительный мир
- 5. Задачи проекта:1. Изучить необходимый теоретический материал об
- 6. Две стихии математикиДве стихии господствуют в математике
- 7. Алексис Клеро (7.5.1713 - 17.5.1765 гг.) - французский математик,
- 8. В 15 веке француз Никола Шюке (1445-1500
- 9. Римская система счисленияMCMXCV = 1000+(1000-100)+(100-10)+5=1995MDCCCCLXXXXV=1000+500+100+100+100+100+50+10+10+10+10+5=1995MVM=1000+(1000-5)=1995 MDVD=1000+500+(500-5)=1995
- 10. Появление названия чиселУченые считают, что сначала название
- 11. Египетская числовая системаВ египетской числовой системе ключевые числа 1, 10, 100 изображались специальными значками - иероглифами.
- 12. По мере увеличения числа,
- 14. Внесистемные числаКроме чисел, записанных при помощи латинских
- 15. Числа - великаны в жизни
- 16. Число клеток в кубике сахара будет- несколько десятков триллионов.
- 17. Во всех, когда-либо отпечатанных книгах за всю историю книгопечатания, около 100 триллионов букв.
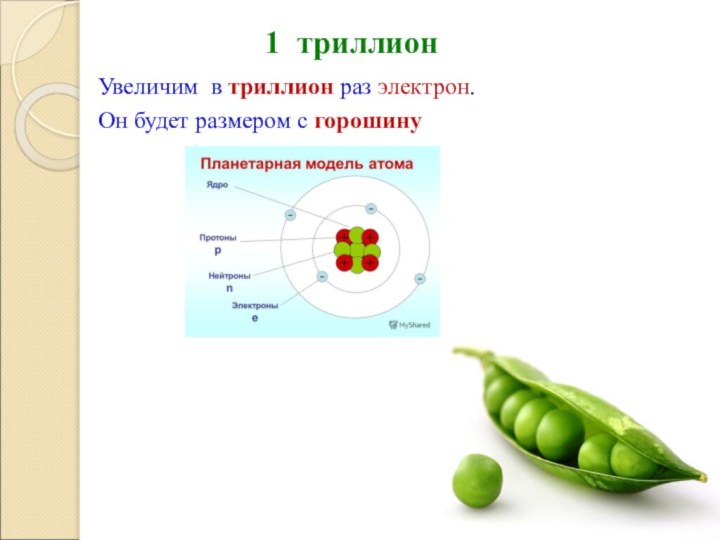
- 18. 1 триллион Увеличим в триллион раз электрон. Он будет размером с горошину
- 19. Квадриллион = 1 000 000 000 000
- 20. Как велик квадриллионОдним квадриллионом кирпичей можно покрыть
- 21. Квинтиллион = 1 000 000 000 000
- 22. Для того чтобы вычерпать все мировые океаны, достаточно 7 квинтиллионов стаканов.
- 23. Если мы возьмем квинтиллион молекул чернил, то сможем написать ими какое-нибудь одно, не очень большое.
- 24. 25 - 30 квинтиллионов молекул содержится в 1 куб.см воздуха при нормальной температуре и давлении.
- 25. Масса всей атмосферы Земли - около 5 квинтиллионов килограммов.
- 26. Число возможных комбинаций в кубике Рубика – 43 квинтилиона с лишним.
- 27. Громадные числа окружают нас повсюду, от просторов
- 28. Большие числа в легендах Возникновение шахматной доски
- 30. Задача 1Самая маленькая птица в мире –
- 31. Задача 22 тонны нефти могут загрязнить 24
- 32. Задача 3Длина Земной окружности составляет 40 000
- 33. Задача 4.Сколько времени потребуется человеку, чтобы сосчитать
- 34. Задача №5. В нашей стране проживают около
- 35. Заключение Проделанная исследовательская работа помогла нам узнать,
- 36. Скачать презентацию
- 37. Похожие презентации
«В сочетании цифр есть безусловная магия, не чувствуют ее лишь люди, начисто лишенные воображения»Борис Акунин «Весь мир театр»

































Слайд 3
Актуальность:
в школьном курсе «математика» не изучается
тема «числа - великаны», но узнав, что существуют числа
больше триллиарда, у нас возник интерес и желание больше узнать об этих числах.Цель:
познакомиться с названием чисел – великанов; научиться их читать; выяснить, какое существует самое большое число, которое имеет собственное название.
Слайд 4
Объект исследования:
удивительный мир чисел.
Предмет исследования:
числа – великаны.
Гипотеза:
изучив историю
возникновения чисел, системы счисления и название классов, сможем читать и писать большие числа, сталкиваясь на практике с числами- великанами на уроках физики, биологии, астрономии.
Слайд 5
Задачи проекта:
1. Изучить необходимый теоретический материал об истории
возникновения чисел и о числах -великанах.
2. Рассмотреть примеры гигантских
чисел в реальном мире.3. Освоить навыки работы с числами - великанами.
Слайд 6
Две стихии математики
Две стихии господствуют в математике –
числа и фигуры с их бесконечным многообразием свойств и
взаимосвязей.Само возникновение понятия числа - одно из гениальнейших проявлений человеческого разума.
Пифагор
Архимед
Карл Гаусс
Слайд 7
Алексис Клеро
(7.5.1713 - 17.5.1765 гг.) - французский математик,
работы которого имели большое значение для астрономии.
Эвари́ст Галуа́ —
(31.05.1832 гг.) - французский математик, основатель современной высшей математики.
Слайд 8 В 15 веке француз Никола Шюке (1445-1500 г.г)
в работе «Наука о числах в трёх книгах» рассматривал
степени с отрицательными и нулевыми показателями.
Слайд 9
Римская система счисления
MCMXCV = 1000+(1000-100)+(100-10)+5=1995
MDCCCCLXXXXV=1000+500+100+100+100+100+50+10+10+10+10+5=1995
MVM=1000+(1000-5)=1995
MDVD=1000+500+(500-5)=1995
Слайд 10
Появление названия чисел
Ученые считают, что сначала название получили
только числа один и два. А все, что шло
после двух, называлось «много».
Слайд 11
Египетская числовая система
В египетской числовой системе ключевые числа
1, 10, 100 изображались специальными значками - иероглифами.
Слайд 12
По мере увеличения числа, нужны
были все новые и новые знаки. Один из первых,
кто научился называть громадные числа, был древнегреческий математик Архимед.
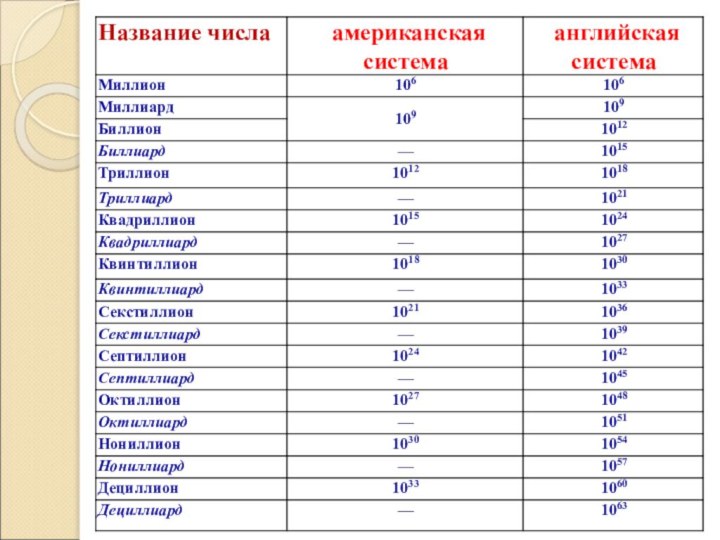
Слайд 14
Внесистемные числа
Кроме чисел, записанных при помощи латинских префиксов
по американской или английской системе, известны и так называемые
внесистемные числа.
Слайд 15
Числа - великаны в жизни
Триллион
= 1000000000000 = 10¹².
Если мы возьмем триллион бактерий,
то они займут объем примерно одного кубика сахара. Слайд 17 Во всех, когда-либо отпечатанных книгах за всю историю
книгопечатания, около 100 триллионов букв.
Слайд 19 Квадриллион = 1 000 000 000 000 000
= 10¹⁵.
Это название уже не на слуху и редко
кто пользуется им в обыденной жизни. Даже не понятно, что может стоить так много. На нашей планете живет примерно квадриллион муравьев.
Разве что небольшая гора высотой метров в 200, состоящая из цельного куска платины.
Слайд 20
Как велик квадриллион
Одним квадриллионом кирпичей можно покрыть все
материки равномерным сплошным пластом высотой почти в четыре этажа.
Чтобы изготовить столько кирпичей завод должен производить в год по 5 миллиардов кирпичей и работать 200 миллионов лет.Слайд 21 Квинтиллион = 1 000 000 000 000 000
000 = 10¹⁸.
Квинтиллион километров - это примерно диаметр
нашей галактики, которая называется Млечный Путь .
До нашей соседки - галактики Андромеды –
25 квинтиллионов.
Слайд 23 Если мы возьмем квинтиллион молекул чернил, то сможем
написать ими какое-нибудь одно, не очень большое.
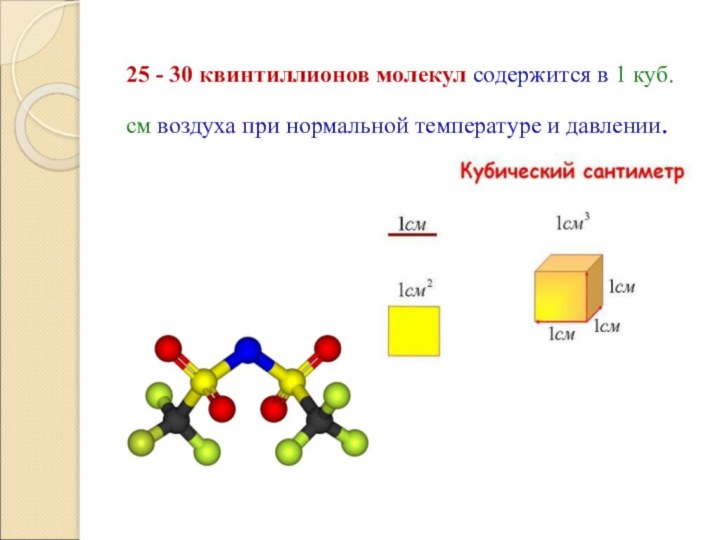
Слайд 24 25 - 30 квинтиллионов молекул содержится в 1
куб.см воздуха при нормальной температуре и давлении.
Слайд 27 Громадные числа окружают нас повсюду, от просторов космоса
до масштабов микромира. Когда мы размышляем об этом, то
поневоле восхищаемся тем, каким удивительным образом устроена ВселеннаяСлайд 29
Практическая часть
Цель: показать на примере задач, как применяются числа-великаны
в жизни и для каких вычислений их используют. Задачи практической части:
1.Узнать, что можно измерять числами-великанами.
2. Определить частоту использования чисел-великанов.
Слайд 30
Задача 1
Самая маленькая птица в мире – колибри,
делает 80 взмахов крыльев в секунду. Сколько взмахов за
5 лет сделает эта птичка?Решение:
1) 80 * 60 = 4800 (в минуту)
2) 4800 * 60 = 288 000 (в час)
3) 288 000 * 24 = 6 912 000 (в сутки)
4) 6 912 000 * 365 = 2 522 880 000 (в год)
5) 2 522 880 000 * 5 = 12 614 400 000 (за 5 лет)
Ответ: 12 614 400 000 взмахов.
Слайд 31
Задача 2
2 тонны нефти могут загрязнить 24 кв.
км поверхности океана. За последний год в океан попало
около 8 миллионов тон нефти. Сколько квадратных километров морской поверхности будет загрязнено за 13 таких лет?Решение:
1) 24 : 2 = 12 (кв. км загрязняет 1 т нефти)
2) 12 * 8 000 000 = 96 000 000 (кв. км загрязняют 8 млн. т нефти)
3) 96 000 000 * 13 = 1 248 000 000 (кв. км загрязнят 8 млн. т нефти за 13 лет)
Ответ: 1 248 000 000 км².
Слайд 32
Задача 3
Длина Земной окружности составляет 40 000 км.
Какое количество секунд понадобилось бы пешеходу, задумавшему совершить кругосветное
путешествие, если каждые сутки он бы преодолевал 25 км?Решение:
1) 40 000 : 25 = 1600 (суток потребуется пешеходу)
2) 1600 * 24 = 38 400 (часов потребуется пешеходу)
3) 38 400 * 60 = 2 304 000 (минут потребуется пешеходу)
4) 2 304 000 * 60 = 138 240 000 (секунд потребуется пешеходу)
Ответ: 138 240 000 секунд.
Слайд 33
Задача 4.
Сколько времени потребуется человеку, чтобы сосчитать миллиард
зерен, если он в минуту будет считать по 100
зерен.Решение: По нашему условию, сосчитать до миллиарда человеку потребуется
1 000 000000:100=10 000 000 мин.
Или 10 000 000:60=166 667, т. е. Примерно 170 000 ч. или (170000:24=7000) около 7000 суток, т. е. Более 16 лет беспрерывного счета.
Слайд 34
Задача №5.
В нашей стране проживают около 250
млн. человек. Если все люди встанут в одну шеренгу,
то какой длины будет эта шеренга? Пусть каждый человек занимает место длиной в 50смРешение: 250 000 000•50 =12 500 000 000см, т.е. 125 000 км.