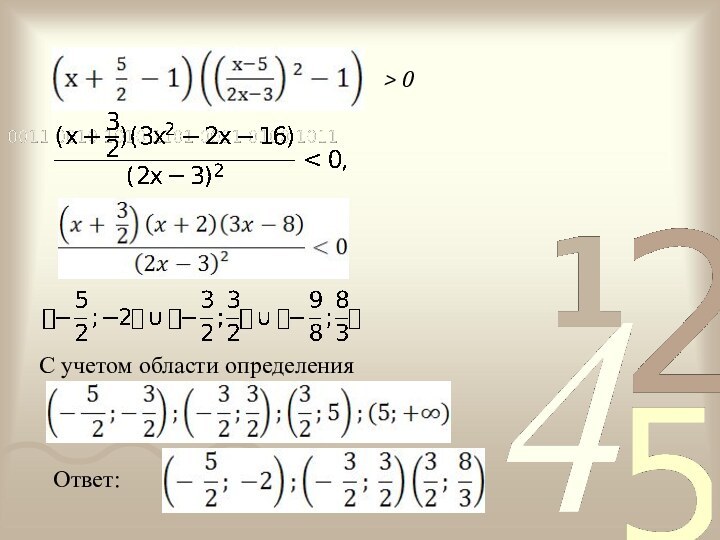логарифмических неравенств в задании С3, в различных сборниках, тренировочных
вариантах ЕГЭ используются, в основном, стандартные методы решения, которые, иногда, трудоемки и занимают много времени.Метод рационализации позволяет упростить и сократить время решения данных неравенств. Этот метод заключается в замене сложного выражения на более простое, равносильное данному на области определения, выражение. Использование данного метода не только упрощает решение, но и сокращает количество ошибок и увеличивает число учащихся, приступающих и решивших задание С3.







![Эффективные методы решения неравенств с одной переменной Пример 3. Решить неравенство: Решение.Ответ: (0;1];(2;+∞)Запишем неравенство используя метод рационализации в виде](/img/tmb/14/1309314/6983a6a656caf134f8a679ac5d0505af-720x.jpg)