Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему проект на тему Графики функций

Содержание

Актуальность проектаПреобразование графиков функции является одним из фундаментальных математических понятийОбучение учащихся построению и преобразованию графиков функции является одной из главных задач обучению математике в школе.
Красота в математике. Графики функций Проектную работу выполнили ученицы 8 «А» класса Актуальность проектаПреобразование графиков функции является одним из фундаментальных математических понятийОбучение учащихся построению Цель проектаРассмотреть графический метод решения уравнений, неравенств, систем уравнений. Научиться строить графики ОпределенияФункцией называют такую зависимостьпеременной у от переменной х, при которой каждомузначению переменной Из истории… Понятие функции уходит своими корнями в ту далёкую Понятие переменной величины было введено в науку французским учёным и математиком Рене Декартом (1596-1650). Линейная функция y=kx+bСвойства функции:D(f)=(- ∞;+∞)E(f)=(- ∞;+∞)Функция монотоннаунаим. - не сущ., унаиб.- не сущ.НепрерывнаяНеограниченная Квадратичная функция у = ax²+bx+cСвойства функции:D(f)=(- ∞;+∞)E(f)=[0;+∞)y=0, при x=0, у>0, при х Функция y= Свойства функции:D(f)=[0;+∞)E(f)=[0;+∞)y=0, при x=0, y>0, при x>0Возрастает на луче Функция y=|x|Свойства функции:D(f)=(- ∞;+∞)E(f)= [ 0;+∞)у=0, при х=0, у>0, при х (- Функция обратной пропорциональности у=Свойства функции:D(f)=(-∞;0) (0;+∞)E(f)= (-∞;0) (0;+∞)у>0 при х>0, y Алгоритм решения уравнений графическим способом.Рассмотреть две функции.В одной системе координат построить графики Пример 1 Решим уравнение графическим способом: Пример 2Решим уравнение графическим способом:x²=x+2y=x²-парабола Алгоритм применения графического метода при решении систем уравненийВыразить у через х в Пример 1Решим систему уравнений графическим способом: Алгоритм решения неравенств графическим методомРассмотреть две функции.В одной системе координат построить графики Пример 1 Решим неравенство графическим способом: Преобразование графиков функцийРазличают три вида геометрических преобразованийграфика функции:Первый вид - масштабирование (сжатие или растяжение) вдоль МасштабированиеМасштабирование - операция сжатия или растяжения графика функции вдоль осей абсцисс и ординат.у=х² - парабола Симметричное (зеркальное) отображение относительно координатных осейу= Параллельный переносПараллельный перенос - сдвиг вдоль осей X и Y.Алгоритм1.Перейти к новой системе координат, проведя (пунктиром) Дробно-линейная функцияДробно-линейной называют обычно функцию вида y= Алгоритм построения графика функции y=|f(x)| Построить график функции y=|f(x)| .Оставить без изменений Пример 1y=| |Построим график функцииy= Пример 2Построить график функции:у= | |у=х 0 1 4 9у 0 1 2 3 Алгоритм решения квадратного уравнения вида ax²+bx+c=0 графическим способом.Рассмотреть квадратичную функцию у= ax²+bx+c. Пример 1х²-4x+3=0a=1 b=-4 c=3X0= = Решим задание из тестов ОГЭПостроить график функции:у= ЗаключениеВ ходе работы над проектом мы познакомились с различными видами функций, систематизировали Список литературыУчебник Алгебра 8 класс А.Г. Мордкович, Н.П. Николаев (2013 год) Часть
Слайды презентации

Слайд 2 Актуальность проекта
Преобразование графиков функции является одним из фундаментальных

Актуальность проектаПреобразование графиков функции является одним из фундаментальных математических понятийОбучение учащихся

математических понятий
Обучение учащихся построению и преобразованию графиков функции является

одной из главных задач обучению математике в школе.

Слайд 3 Цель проекта
Рассмотреть графический метод решения уравнений, неравенств, систем

Цель проектаРассмотреть графический метод решения уравнений, неравенств, систем уравнений. Научиться строить

уравнений. Научиться строить графики с помощью преобразований и графики

функций с модулем.

Задачи

Рассмотреть графики различных функций и их свойства.
Научиться применять графический способ решения:
Уравнений;
систем уравнений;
неравенств.
Изучить способы преобразования графиков.
Научиться строить графики функций с модулем, графики дробно-линейной функции и квадратичной функции.
Подготовиться к сдаче ОГЭ на данную тему.
Систематизировать все знания о функциях и создать диск учебных видеороликов.


Слайд 4 Определения
Функцией называют такую зависимость
переменной у от переменной х,

ОпределенияФункцией называют такую зависимостьпеременной у от переменной х, при которой каждомузначению

при которой каждому
значению переменной x соответствует единственное
значение переменной y.



Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значению аргумента, а ординаты – соответствующим значениям функции.

Слайд 5 Из истории…
Понятие функции уходит своими

Из истории… Понятие функции уходит своими корнями в ту далёкую

корнями в ту далёкую эпоху, когда люди впервые поняли,

что окружающие их предметы взаимосвязаны. Они ещё не умели считать, но уже знали, что:
чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода;
чем сильнее натянута тетива лука, тем дальше полетит стрела;
чем дольше горит костёр, тем теплее в пещере.

Слайд 6 Понятие переменной величины было введено в науку французским

Понятие переменной величины было введено в науку французским учёным и математиком Рене Декартом (1596-1650).

учёным и математиком Рене Декартом (1596-1650).

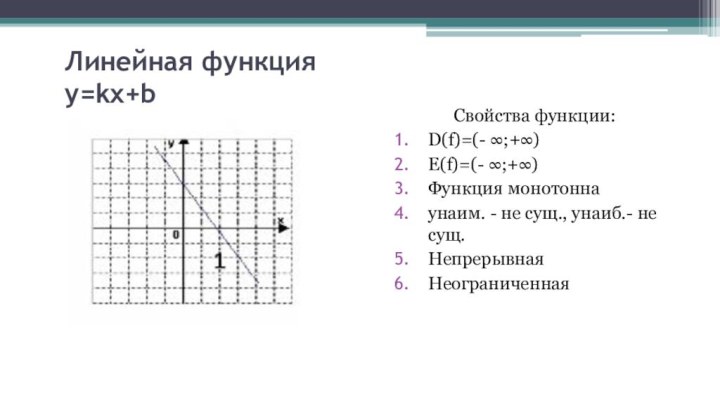
Слайд 7 Линейная функция y=kx+b
Свойства функции:
D(f)=(- ∞;+∞)
E(f)=(- ∞;+∞)
Функция монотонна
унаим. -

Линейная функция y=kx+bСвойства функции:D(f)=(- ∞;+∞)E(f)=(- ∞;+∞)Функция монотоннаунаим. - не сущ., унаиб.- не сущ.НепрерывнаяНеограниченная

не сущ., унаиб.- не сущ.
Непрерывная
Неограниченная

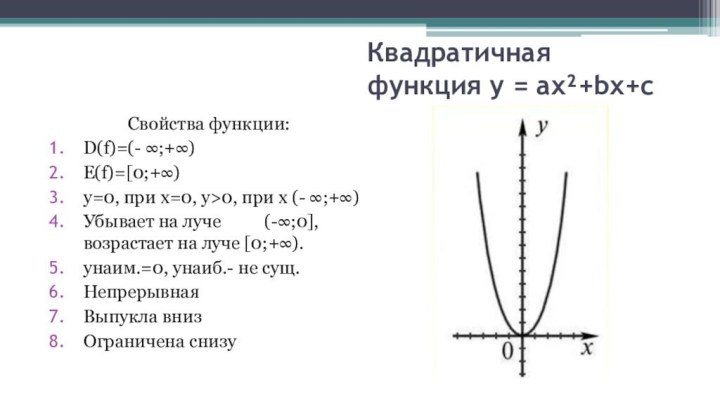
Слайд 8 Квадратичная функция у = ax²+bx+c
Свойства функции:
D(f)=(- ∞;+∞)
E(f)=[0;+∞)
y=0, при

Квадратичная функция у = ax²+bx+cСвойства функции:D(f)=(- ∞;+∞)E(f)=[0;+∞)y=0, при x=0, у>0, при

x=0, у>0, при х (- ∞;+∞)
Убывает на луче

(-∞;0], возрастает на луче [0;+∞).
унаим.=0, унаиб.- не сущ.
Непрерывная
Выпукла вниз
Ограничена снизу

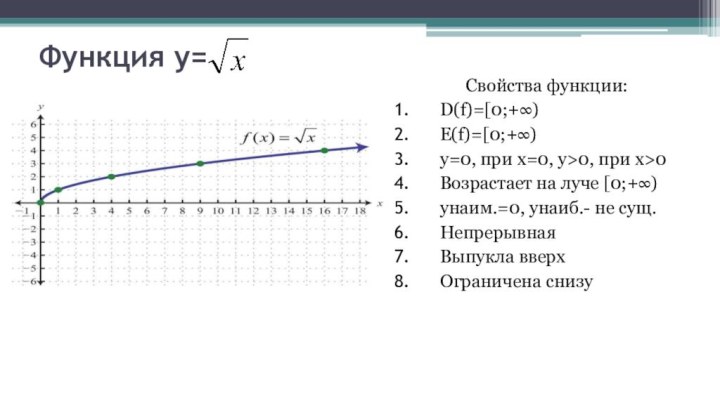
Слайд 9 Функция y=
Свойства функции:
D(f)=[0;+∞)
E(f)=[0;+∞)
y=0, при x=0, y>0,

Функция y= Свойства функции:D(f)=[0;+∞)E(f)=[0;+∞)y=0, при x=0, y>0, при x>0Возрастает на луче

при x>0
Возрастает на луче [0;+∞)
унаим.=0, унаиб.- не сущ.
Непрерывная
Выпукла вверх
Ограничена

снизу

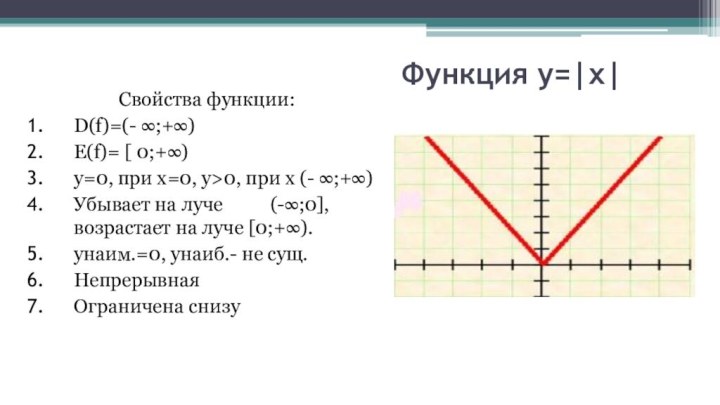
Слайд 10 Функция y=|x|
Свойства функции:
D(f)=(- ∞;+∞)
E(f)= [ 0;+∞)
у=0, при х=0,

Функция y=|x|Свойства функции:D(f)=(- ∞;+∞)E(f)= [ 0;+∞)у=0, при х=0, у>0, при х

у>0, при х (- ∞;+∞)
Убывает на луче

(-∞;0], возрастает на луче [0;+∞).
унаим.=0, унаиб.- не сущ.
Непрерывная
Ограничена снизу


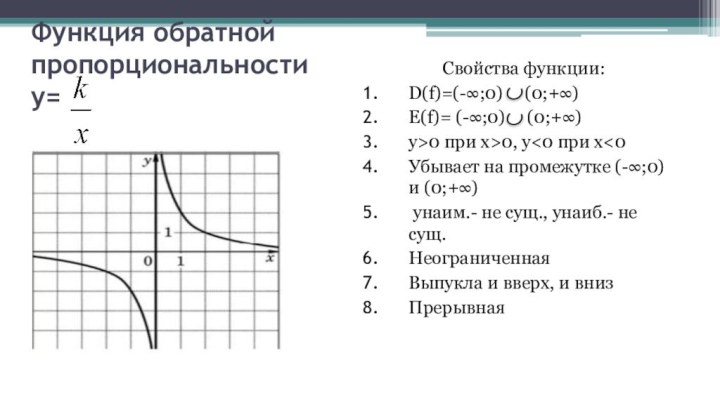
Слайд 11 Функция обратной пропорциональности у=
Свойства функции:
D(f)=(-∞;0) (0;+∞)
E(f)=

Функция обратной пропорциональности у=Свойства функции:D(f)=(-∞;0) (0;+∞)E(f)= (-∞;0) (0;+∞)у>0 при х>0, y

(-∞;0) (0;+∞)
у>0 при х>0, y

на промежутке (-∞;0) и (0;+∞)
унаим.- не сущ., унаиб.- не сущ.
Неограниченная
Выпукла и вверх, и вниз
Прерывная

Слайд 12 Алгоритм решения уравнений графическим способом.
Рассмотреть две функции.
В одной

Алгоритм решения уравнений графическим способом.Рассмотреть две функции.В одной системе координат построить

системе координат построить графики этих функций.
Найти точки пересечения

построенных графиков
Абсциссы точек пересечения – это корни уравнения. Записать их в ответ.

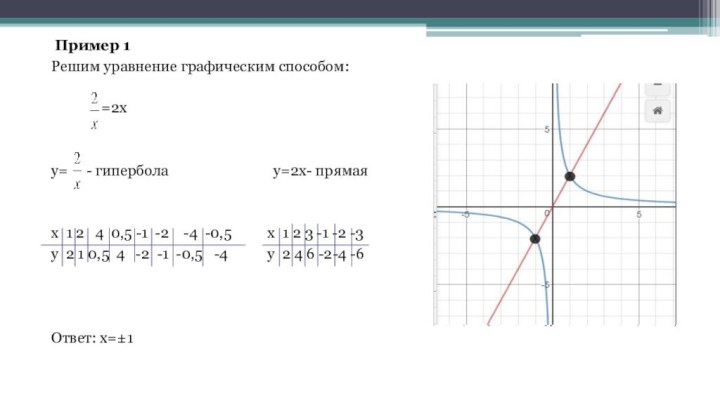
Слайд 13 Пример 1
Решим уравнение графическим способом:

Пример 1 Решим уравнение графическим способом:



=2x


y= - гипербола y=2x- прямая


x 1 2 4 0,5 -1 -2 -4 -0,5 x 1 2 3 -1 -2 -3
y 2 1 0,5 4 -2 -1 -0,5 -4 y 2 4 6 -2-4 -6



Ответ: x=±1

Слайд 14 Пример 2
Решим уравнение графическим способом:

x²=x+2

y=x²-парабола

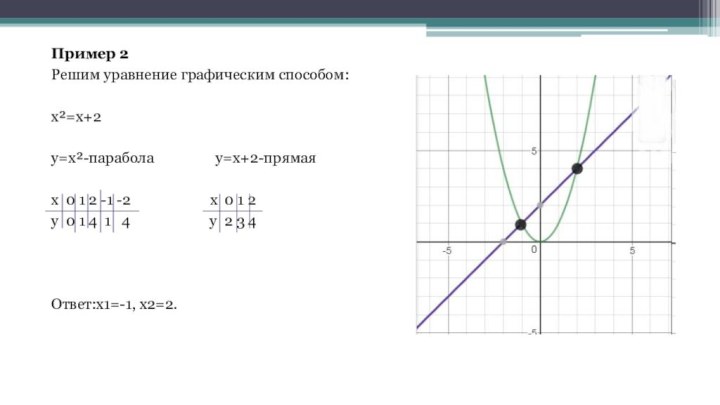
Пример 2Решим уравнение графическим способом:x²=x+2y=x²-парабола y=x+2-прямаяx 0

y=x+2-прямая

x 0 1 2

-1 -2 x 0 1 2
y 0 1 4 1 4 y 2 3 4



Ответ:x1=-1, x2=2.

Слайд 15 Алгоритм применения графического метода при решении систем уравнений
Выразить

Алгоритм применения графического метода при решении систем уравненийВыразить у через х

у через х в каждом уравнении.
Построить в одной системе

координат графики этих функций.
Определить координаты всех точек пересечений графиков (если они есть).
Координаты этих точек и будут решениями системы.

Слайд 16 Пример 1
Решим систему уравнений графическим способом:

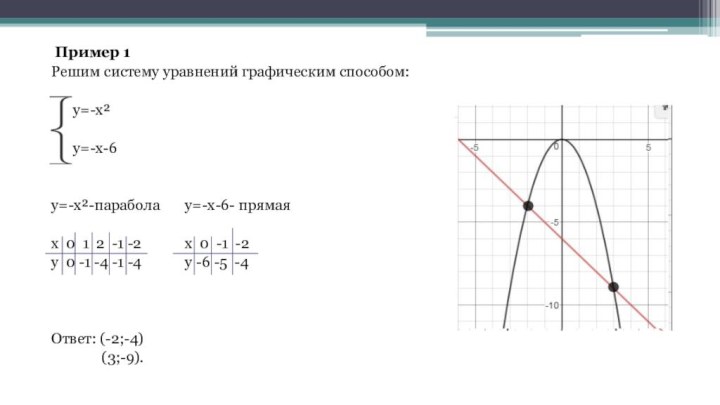
Пример 1Решим систему уравнений графическим способом: y=-x²



y=-x²


y=-x-6


y=-x²-парабола y=-x-6- прямая

x 0 1 2 -1 -2 x 0 -1 -2
y 0 -1 -4 -1 -4 y -6 -5 -4



Ответ: (-2;-4)
(3;-9).

Слайд 17 Алгоритм решения неравенств графическим методом
Рассмотреть две функции.
В одной

Алгоритм решения неравенств графическим методомРассмотреть две функции.В одной системе координат построить

системе координат построить графики этих функций.
Определить абсциссы точек

пересечения графиков (приближённо).
Определить промежуток, на котором график 1-й функции лежит выше или ниже 2-й функции (в соответствии со знаком неравенства).
Записать полученное множество в ответ.

Слайд 18 Пример 1
Решим неравенство графическим способом:

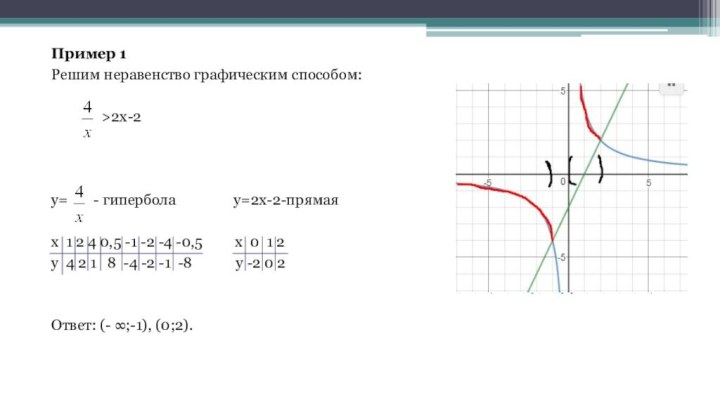
Пример 1 Решим неравенство графическим способом: >2х-2


>2х-2



у= - гипербола у=2х-2-прямая

х 1 2 4 0,5 -1 -2 -4 -0,5 х 0 1 2
у 4 2 1 8 -4 -2 -1 -8 y -2 0 2


Ответ: (- ∞;-1), (0;2).

Слайд 19 Преобразование графиков функций
Различают три вида геометрических преобразований
графика функции:
Первый вид

Преобразование графиков функцийРазличают три вида геометрических преобразованийграфика функции:Первый вид - масштабирование (сжатие или растяжение)

- масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
Второй вид

- симметричное (зеркальное) отображение относительно координатных осей.
Третий вид - параллельный перенос (сдвиг) вдоль осей Х и У.

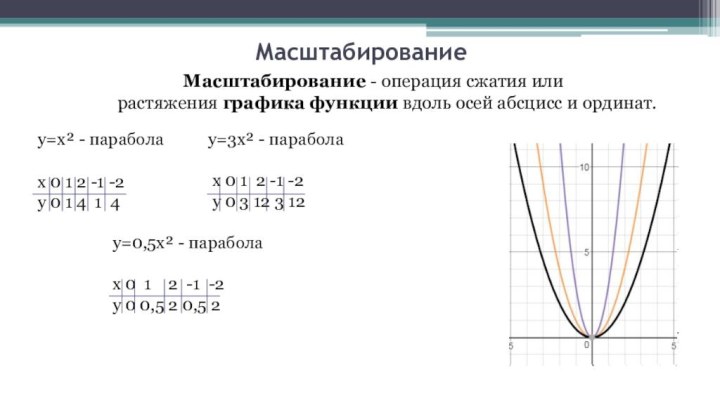
Слайд 20 Масштабирование
Масштабирование - операция сжатия или растяжения графика функции вдоль осей абсцисс и

МасштабированиеМасштабирование - операция сжатия или растяжения графика функции вдоль осей абсцисс и ординат.у=х² - парабола

ординат.
у=х² - парабола



х 0 1 2 -1 -2
у 0 3 12 3 12

у=0,5х² - парабола

х 0 1 2 -1 -2
у 0 0,5 2 0,5 2








у=3х² - парабола

х 0 1 2 -1 -2
у 0 1 4 1 4

Слайд 21 Симметричное (зеркальное) отображение относительно координатных осей
у=

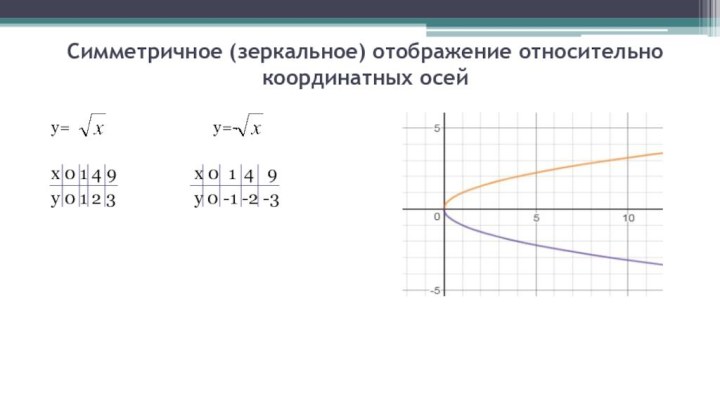
Симметричное (зеркальное) отображение относительно координатных осейу=

у=-

х 0 1 4 9 х 0 1 4 9
у 0 1 2 3 у 0 -1 -2 -3

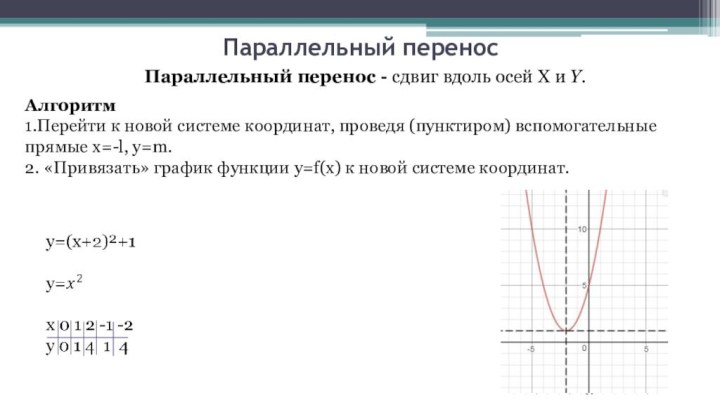
Слайд 22 Параллельный перенос
Параллельный перенос - сдвиг вдоль осей X и Y.
Алгоритм
1.Перейти к новой

Параллельный переносПараллельный перенос - сдвиг вдоль осей X и Y.Алгоритм1.Перейти к новой системе координат, проведя

системе координат, проведя (пунктиром) вспомогательные прямые x=-l, y=m.
2. «Привязать»

график функции y=f(x) к новой системе координат.

Слайд 23 Дробно-линейная функция
Дробно-линейной называют обычно функцию вида y=

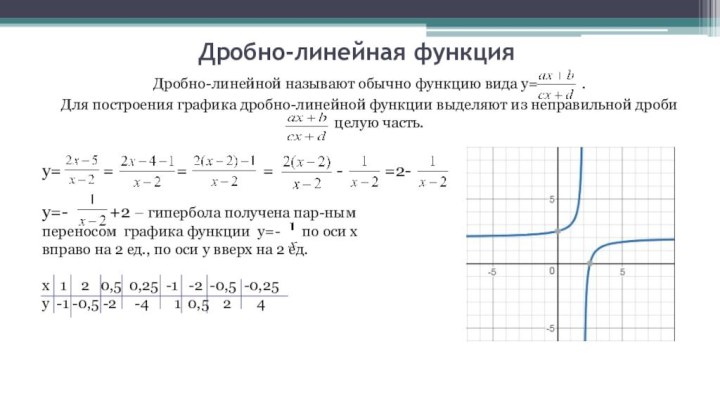
Дробно-линейная функцияДробно-линейной называют обычно функцию вида y= .Для построения

.
Для построения графика дробно-линейной функции

выделяют из неправильной дроби целую часть.

y= = = = - =2-

y=- +2 – гипербола получена пар-ным
переносом графика функции y=- по оси х
вправо на 2 ед., по оси у вверх на 2 ед.

х 1 2 0,5 0,25 -1 -2 -0,5 -0,25
у -1 -0,5 -2 -4 1 0,5 2 4








Слайд 24 Алгоритм построения графика функции y=|f(x)|
Построить график функции

Алгоритм построения графика функции y=|f(x)| Построить график функции y=|f(x)| .Оставить без

y=|f(x)| .
Оставить без изменений те части графика функции y=f(x),

которые лежат не ниже оси x.
Части графика функции y=f(x), которые лежат ниже оси x, заменить на симметричные им относительно оси x.

Алгоритм построения графика функции y=f(|x|)

Построить график функции y=f(x) при x 0.
Добавить ветви, симметричные построенным относительно оси y.


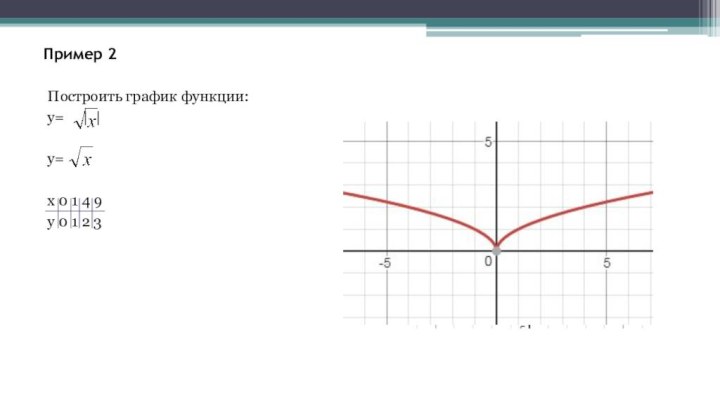
Слайд 25 Пример 1
y=| |

Построим график функции

y=

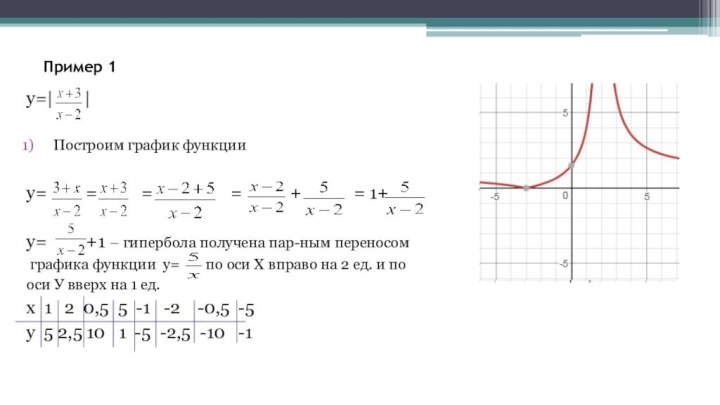
Пример 1y=| |Построим график функцииy= =

=

= = + = 1+

y= +1 – гипербола получена пар-ным переносом
графика функции y= по оси Х вправо на 2 ед. и по
оси У вверх на 1 ед.
х 1 2 0,5 5 -1 -2 -0,5 -5
у 5 2,5 10 1 -5 -2,5 -10 -1



Слайд 26 Пример 2
Построить график функции:
у= | |

у=

х

Пример 2Построить график функции:у= | |у=х 0 1 4 9у 0 1 2 3

0 1 4 9
у 0 1 2 3

Слайд 27 Алгоритм решения квадратного уравнения вида ax²+bx+c=0 графическим способом.
Рассмотреть

Алгоритм решения квадратного уравнения вида ax²+bx+c=0 графическим способом.Рассмотреть квадратичную функцию у=

квадратичную функцию у= ax²+bx+c. Найти координаты вершины параболы, построить

на координатной плоскости соответствующую точку, провести ось параболы.
Отметить на оси х 4 точки, симметричные относительно оси параболы.
Через полученные точки провести параболу.
Координаты точек пересечения параболы с осью Х и будут решением уравнения.

Слайд 28 Пример 1
х²-4x+3=0
a=1 b=-4 c=3
X0=

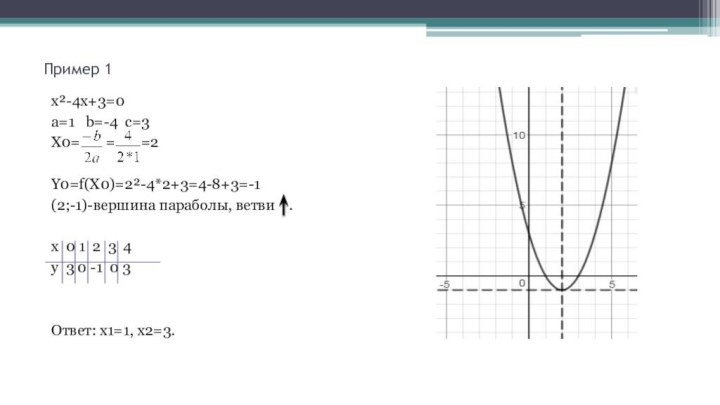
Пример 1х²-4x+3=0a=1 b=-4 c=3X0= = =2Y0=f(X0)=2²-4*2+3=4-8+3=-1(2;-1)-вершина параболы, ветви .х

= =2

Y0=f(X0)=2²-4*2+3=4-8+3=-1
(2;-1)-вершина параболы, ветви .

х

0 1 2 3 4
у 3 0 -1 0 3


Ответ: х1=1, х2=3.

Слайд 29 Решим задание из тестов ОГЭ
Построить график функции:

у=

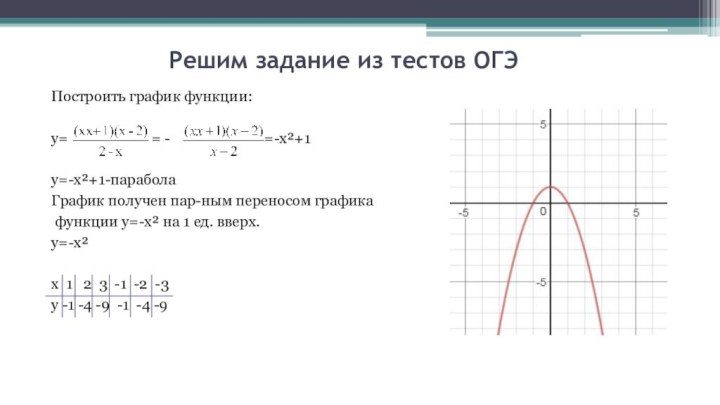
Решим задание из тестов ОГЭПостроить график функции:у=

= - =-х²+1

у=-х²+1-парабола
График получен пар-ным переносом графика
функции у=-х² на 1 ед. вверх.
у=-х²

х 1 2 3 -1 -2 -3
у -1 -4 -9 -1 -4 -9

Слайд 30 Заключение
В ходе работы над проектом мы познакомились с

ЗаключениеВ ходе работы над проектом мы познакомились с различными видами функций,

различными видами функций, систематизировали всю информацию о них. Изучили

применение графического способа при решении уравнений, неравенств, систем уравнений, квадратных уравнений, которое мы представили в своей работе. Практическая значимость нашей работы заключается в том, что мы создали диск учебных видеороликов, который может использоваться учащимися 8-х и 9-х классов.
  • Имя файла: prezentatsiya-proekt-na-temu-grafiki-funktsiy.pptx
  • Количество просмотров: 171
  • Количество скачиваний: 8
- Предыдущая Презентация к уроку окружающего мира Путешествие по странам. Италия
Следующая - Презентация по окружающему миру на тему Лекарственные растения Тамбовской области

Похожие презентации

Презентация по математике на тему Виды чисел Презентация по математике на тему Виды чисел 189
Урок 26(71). Вычитание суммы из числа Урок 26(71). Вычитание суммы из числа 105
Презентация по математике на тему Числа 6 и 7 1 класс Презентация по математике на тему Числа 6 и 7 1 класс 128
Презентация к уроку по теме: Деление с остатком Презентация к уроку по теме: Деление с остатком 118
Аттестационная работа. Графика квадратной функции, содержащей модуль методическая разработка занятия курса. 9 класс Аттестационная работа. Графика квадратной функции, содержащей модуль методическая разработка занятия курса. 9 класс 100
Деление рациональных чисел Деление рациональных чисел 112
Обыкновенные дифференциальные уравнения Обыкновенные дифференциальные уравнения 128
geom geom 167
Презентация Подготовка к ВПР 6 класс Презентация Подготовка к ВПР 6 класс 155
Презентация Игра Найди предмет похожий на прямоугольник презентация к уроку по математике (средняя группа) Презентация Игра Найди предмет похожий на прямоугольник презентация к уроку по математике (средняя группа) 146
Деление до 20 Деление до 20 92
Презентация по математике презентация к уроку по математике (1 класс) Презентация по математике презентация к уроку по математике (1 класс) 92
Дифференцирование частного и степени Дифференцирование частного и степени 81
Тригонометрические формулы (10 класс) Тригонометрические формулы (10 класс) 120
презентация От игры - к знаниям (ФЭМП) презентация к уроку по математике (старшая группа) презентация От игры - к знаниям (ФЭМП) презентация к уроку по математике (старшая группа) 55
Умножение рациональных чисел Умножение рациональных чисел 223
Степень с натуральным показателем Степень с натуральным показателем 98
НОД по ФЭМП в старшей группе для детей с ТНР презентация к занятию по математике (старшая группа) НОД по ФЭМП в старшей группе для детей с ТНР презентация к занятию по математике (старшая группа) 138
Площадь многоугольника Площадь многоугольника 102
Презентация Экологическая составляющая уроков математики Презентация Экологическая составляющая уроков математики 132
Как измерить расстояние между родственниками Как измерить расстояние между родственниками 131
Процент Процент 108
Презентация к уроку математики 3 класс по теме:Арифметические действия с трёхзначными числами презентация к уроку математики (3 класс) Презентация к уроку математики 3 класс по теме:Арифметические действия с трёхзначными числами презентация к уроку математики (3 класс) 140
Что мы знаем о числах великанах? Что мы знаем о числах великанах? 125
Проект по математике на тему Узоры и орнаменты. Проект по математике на тему Узоры и орнаменты. 109
Точки на осях координат Точки на осях координат 120
Презентации по таблице умножения и деления с числами 2-6 Для умников и умниц Презентации по таблице умножения и деления с числами 2-6 Для умников и умниц 112
Презентация к исследовательской работе на тему Лес - наше богатство Берегите лес Презентация к исследовательской работе на тему Лес - наше богатство Берегите лес 110
Отбор корней в тригонометрических уравнениях Отбор корней в тригонометрических уравнениях 166
Презентация Вычитание числа 4 Презентация Вычитание числа 4 101