∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙
3 ∙ 3 ∙ 31,5 ∙ 1,5 ∙ 1,5 ∙ 1,5 ∙ 1,5 ∙ 1,5
(-2с) ∙(-2с) ∙ (-2с) ∙ (-2с) ∙(-2с)
(х+y) ∙ (х+y) ∙ (х+y) ∙ (х+y)
= 39
=(-2с)5
= 1,56
=(х+y)4
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



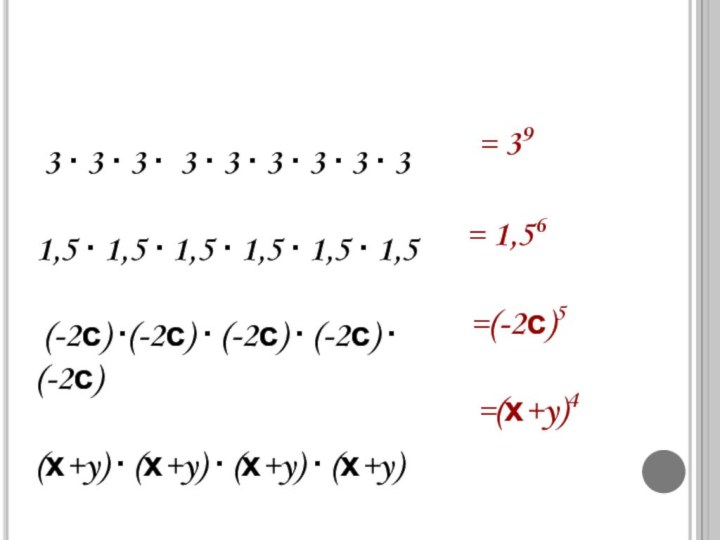




























= 39
=(-2с)5
= 1,56
=(х+y)4
= 0,36
= (-ac)5
= 510
= (x + 3)4
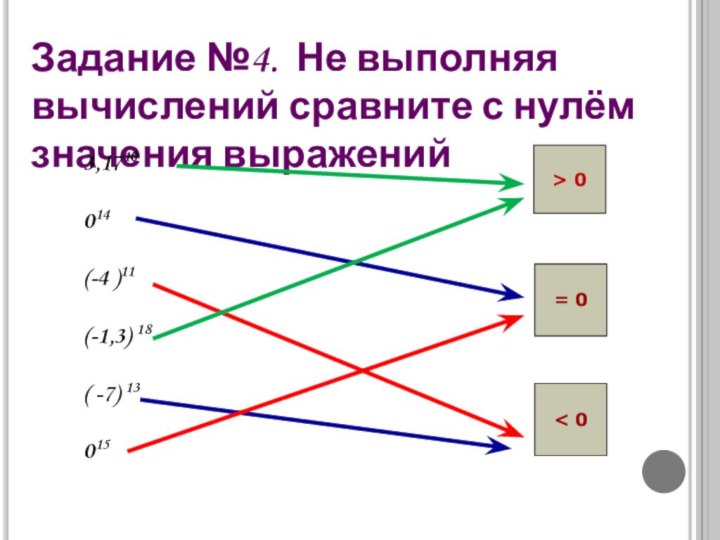
= 0
< 0
При переводе
единиц измерения:
72 км = 72000 м = 72∙103 м
5кг = 5000 г = 5∙103г