Слайд 2
Содержание
Введение.
Математические вычисления в строительстве.
История взаимосвязи математики и
строительства.
Некоторые виды математических задач в строительном деле.
Определение площади
нестандартной формы.
Определение количества и стоимости расходного материала.
Задачи на оптимизацию расходов в строительном деле.
Использование «Золотого сечения» в строительстве.
Математический смысл «Золотого сечения».
История «Золотого сечения».
Использование «Золотого сечения» в мировой архитектуре.
«Золотое сечение» в архитектурных сооружениях г.Алматы.
Проект детской игровой площадки «Құлыншақ».
Заключение.
Литература.
Слайд 3
Актуальность исследования
Объект исследования
Предмет исследования
Цель исследования
Методы исследования
Практическая значимость
Развитие взаимосвязи математики

и строительного дела; необходимость решения задач с практическим содержанием
для более глубокого, не формального изучения основ математики.
Строительство и архитектурные сооружения.
Применение математических знаний при проектировании и строительстве архитектурных сооружений.
Показать использование математических знаний в строительстве и при проектировании архитектурных сооружений, рассмотреть архитектуру с точки зрения «Золотого сечения»
Изучение и анализ теоретических сведений по данному вопросу. Наблюдение, сравнение, сопоставление, анализ, аналогия. Анкетирование, опрос. Измерительные работы и расчеты, анализ полученных результатов.
Данный материал можно использовать в школе для привития интереса учащихся к математике и формирования у них представления о прикладных возможностях математики, её связи с архитектурой. Разработанный проект детской площадки можно реализовать во дворах домов, школ, детских садов.
Слайд 4
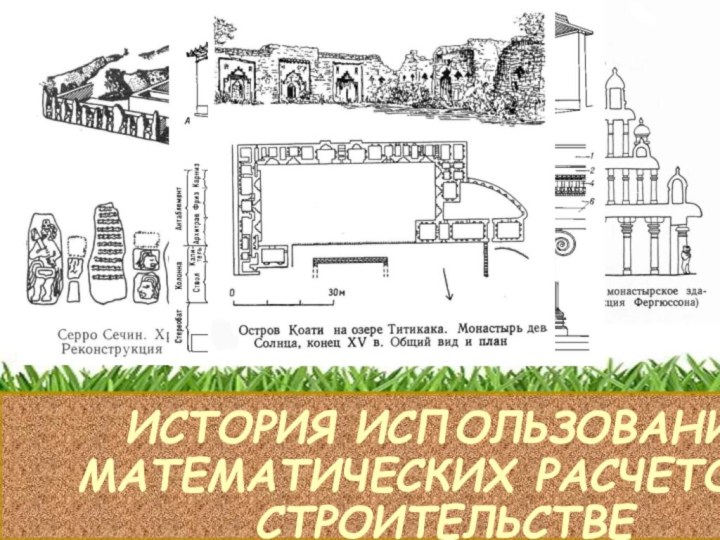
История использования Математических расчетов в строительстве
стория взаимосвязи математики
и строительства.
Слайд 5
Взаимосвязь архитектуры и математики прослеживается на протяжении
всей истории человечества.
Строительство и архитектура зарождаются вместе с
человечеством, сопровождают его в историческом развитии.
Слайд 7
Собор святого Петра в Ватикане
Слайд 8
Некоторые виды математических задач в строительном деле
В строительном
деле возникает огромное количество задач различной сложности, решаемых с
использованием математических знаний. В нашей работе мы рассмотрим только несколько простых видов прикладных задач, которые чаще встречаются в деятельности строителя-практика. С подобными вопросами может столкнуться и профессионал, и любитель, затеявший несложный капитальный ремонт.
Слайд 9
Принцип деления сложной геометрической фигуры на несколько простых
Определение
площади нестандартной формы
Слайд 10
Нахождение площадей простых фигур.
Слайд 11
ЗАДАЧА
Дано: Дом; h - 3 м.; 2 окна;
S окна - 1,5х2м; дверь; S двери - 1х2,3м
Решение.
Основание
дома составляют две геометрические фигуры: полуокружность радиусом 3,5 м и прямоугольник со сторонами 10 и 16 метров.
Чтобы найти площадь стен дома надо найти общую площадь боковой поверхности дома и вычесть площади окон и двери:
Sстен = Sбок.пов. – Sокон – Sдвери ;
S бок.пов. = Pоснов. · h ; P основ. = Pпрям + l/2 - 2r; l = 2πr;
Следовательно,
S бок.пов. = (Pпрям + πr - 2r) · h = (2ab + r(π-2))·h,
где h – высота стен, l – длина окружности, r – радиус окружности, a и b – стороны прямоугольника
Тогда
S бок.пов. = (2 · (16 + 10) + 3,5 · (3,14 – 2)) · 3 = 167,97 ≈168 (м2),
Sокон = 2 · 1,5 ·2 = 6 (м2), Sдвери = 1 · 2,5 = 2,5 (м2),
Sстен = 168 – 6 – 2,5 = 159,5 (м2).
Ответ: площадь стен дома составляет 159,5 м2.
Вычислить: площадь стен для облицовки
Слайд 12
Алгоритм решения задач вычисления площади нестандартной фигуры
Разбить фигуру
на множество стандартных фигур.
Найти площадь каждой из полученных стандартных
фигур.
Найти сумму этих площадей.
Вычесть из этой суммы площади форм, не входящих в эту фигуру (например, окна, двери и т.д.).
Слайд 13
Строители часто встречаются с задачей определения количества и
стоимости расходного материала для строительства или отделки стен или
пола.
Определение количества расходного материала
Слайд 14
Задача 1. Сколько краски понадобится, чтобы покрасить стену
размером 3м х 4м в два слоя, расход краски
0,07 кг/м2.
Решение.
1) S = 3м·4м = 12м2;
2) 0,07 · 12 = 0,84кг;
3) 0,84 · 2 = 1,68кг;
Ответ: Достаточно одной двухкилограммовой банки краски.
Задача 2.
Необходимо выложить кафельной плиткой пол в ванной комнате. Размер пола: 3х3,5м. Размер плитки 40х40см. Сколько кафельной плитки понадобится?
Решение:
1. Найдѐм площадь пола: Sпола = 3 ·3,5 = 10,5м2;
2. Площадь одной плитки: Sплитки = 0,4 · 0,4 = 0,16м2;
3. Определим, сколько плиток понадобится:
N = Sпола : Sплитки = 10,5 : 0,16 = 65,625 ≈ 66 штук.
Ответ: нужно примерно 66 плиток.
Слайд 15
Алгоритм решения задач на определение количества расходного материала
при
покраске, штукатурке, побелке и т.д.:
1. Определить общую площадь поверхности
(S) для отделки.
2. Рассчитать количество расходного материала на единицу площади (Е).
3. Полученную величину умножить на площадь поверхности (K=S·E).
при облицовке (кирпичом, плиткой и т.д.):
1. Вычислить общую площадь поверхности (S) для отделки.
2. Определить площадь единицы расходного материала (Sм – площадь одной облицовочной плитки);
3. Найти количество расходного материала (N – количество облицовочных плиток) как частное: N=S : Sм.
Слайд 16
Задачи на оптимизацию расходов материала в строительном деле
Под
"оптимизацией" мы подразумеваем выбор вариантов строительной деятельности в целях
минимизирования финансовых затрат и поиск различных путей экономии с учетом математических вычислений.
Известно, что более 60% прямых затрат в строительстве занимают материалы, поэтому задача оптимизации расходов строительства является актуальной, поскольку с ростом цен на материалы возрастает и стоимость жилья.
Слайд 17
Задача 1.
Выше был приведен пример задачи на определение
площади стен дома в целях их облицовки. Теперь решим
следующую задачу.
Перед нами стоит выбор: облицовка кирпичом или облицовка сайдингом. Найти самый экономичный вариант отделки.
Решение.
Мы определили, что общая площадь стен дома составляет 160 м2. Расчитаем стоимость материалов при облицовке кирпичом и сайдингом.
Стоимость 1 облицовочного кирпича- 40 тг. На 1 м² требуется 52 кирпича, площадь стен дома – 160 (м2), тогда 52 · 40 · 160 = 332 800 тг – стоимость кирпича на полную облицовку стен.
Стоимость сайдинга 1800 тг за 1 м², тогда 18000 · 160 = 288 000 тг – стоимость сайдинга на полную облицовку стен.
Ответ: наиболее экономичным является вариант облицовки стен сайдингом.
Слайд 18
Пусть от прежней стены сохраняется x метров, а

остальные 12 - x метров разбиваются так, чтобы из
полученного материала возвести заново часть стены нового дома. Если стоимость кладки погонного метра стены из нового материала равна а, то ремонт x метров старой стены будет стоить ах/4; возведение участка длиной 12 – х будет стоить а(12 – х)/2 ; прочей части этой стены а[у – (12 – х)], т.е. а(у + х – 12); третьей стены ах, четвертой ау. Вся работа обойдется в ax/4+a*(12-x)/2+a(y-x+12)+ax+ay=a(7x+8y)/4-6a.
Последнее выражение достигает наименьшей величины тогда же, когда будет минимальной и сумма 7х + 8у. Мы знаем, что площадь дома ху равна 112; следовательно, 7х · 8у =56 ·112. При постоянном произведении сумма 7х + 8у достигает наименьшей величины тогда, когда 7х = 8у, откуда у = 7х/8. Подставив это выражения для у в уравнение ху =112, имеем: 7x2/8=112; x2=128; x≈11,3.
А так как длина старой стены 12 м, то подлежит разборке 12 - 11,3 = 0,7 м этой стены.
Ответ: необходимо разобрать 0,7м старой стены.
Задача 2.
На месте разрушенного дома, от которого уцелела стена, надо построить новый. Длина уцелевшей стены – 12 м. Площадь нового дома должна равняться 112 кв. м. Хозяйственные условия работы таковы:
1) Ремонт погонного метра стены обходится в 25% стоимости кладки новой;
2) разбор погонного метра старой стены и кладка из полученного материала новой стены стоит 50% того, во что обходится постройка погонного метра стены из нового материала.
Как при таких условиях наиболее выгодным образом использовать уцелевшую стену?
Решение:
Слайд 19
Общий алгоритм решения задач по оптимизации расхода материала
в строительном деле
1. Выявить все подходящие типы расходного материала
(n вариантов);
2. Рассчитать количество расходного материала каждого из вариантов (K1, K2, …Kn).
3. Определить стоимость расходного материала каждого из вариантов (С1, С2, …Сn).
4. Найти наименьшее значение Сn. Значение n будет соответствовать номеру наиболее оптимального варианта.
Слайд 21
Математический смысл «Золотого сечения»
Золотое сечение — это такое пропорциональное
деление отрезка на неравные части, при котором весь отрезок
так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.
Слайд 22
Числовое значение золотого сечения
На рисунке изображены прямоугольник и
отрезки, соответствующие пропорциям:
Пусть высота h1 = 1, а расстояние от
верхнего края до средней линии обозначим за x (h2 = x). Тогда получим:
1 : x = x : (1 – x)
x2 – x – 1 = 0
Решение этого уравнения:
x1,2 = (1±√5)/2
Положительный корень этого уравнения (√5 + 1) / 2 ≈ 1,618… ,
это и есть приближенное значение «Золотого сечения».
Слайд 23
История «Золотого сечения»
Принято считать, что понятие о золотом
делении ввел в научный обиход Пифагор, древнегреческий философ и
математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.
В дошедшей до нас античной литературе золотое деление впервые упоминается в “Началах” Евклида.
Во времена Ренессанса принципы золотого сечения использовали в своих работах такие известные личности как Леонардо да Винчи и Альбрехт Дюрер.
Слайд 24
Ряд Фибоначчи
Существует тесная связь Золотого сечения с числами
Фибоначчи. Последовательностью Фибоначчи называется последовательность, первые два члена которой равны 1,
а каждый последующий - сумме двух предыдущих. Таким образом, эта последовательность (обозначим ее через {an}) определяется следующим образом:
a1=1, a2=1, an+2=an+1+an; (n=1,2,3, …).
Вот первые члены этой последовательности: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,..., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, отношение любого члена последовательности an (n>3) к предшествующему члену an-1 будет приближаться к значению φ=1.61803398875... при увеличении значения n. Например, 34 : 21 = 1,617, а 55 : 34 = 1,618. То есть это приближение тем лучше, чем больше номер взятого члена. Обратное соотношение an : an+1 = 0,618… .
Слайд 25
Золотое сечение в исторических зданиях
Одним из красивейших произведений
древнегреческой архитектуры является Парфенон.
Если принять за единицу ширину
торцового фасада храма, то основные пропорции фасада Парфенона образуют прогрессию, состоящую из 8 членов ряда: 1:а1:а2:а3:а4:а5:а6:а7 = 1,618... .
Слайд 26
Такое же соотношение наблюдается в пропорциях храма Василия
Блаженного, но в нем за единицу принята высота храма:
: 1:а1:а2:а3:а4:а5:а6:а7 = 1,618... .
Слайд 27
Золотое сечение в современной архитектуре Казахстана
Дворец мира и
согласия — пирамида, созданная архитектором сэром Норманом Фостером в
Астане.
В соответствии с принципом «Золотого сечения Фибоначчи», основанием пирамиды является квадрат, со стороной, равной высоте пирамиды – 61.803399 м., высота пирамиды также составляет 61.803399м. Т.е. в размерах дан коэффициент золотого сечения, умноженный на 100 и выраженный в метрах.
Слайд 28
Триумфальная Арка в Астане, которая символизирует успех молодой
республики за первые 20 лет ее становления и развития.
Высота арки - 20 метров, ширина - 13 метров. За ее основу принята классическая Триумфальная арка.
По размерам арки, указанным на рисунке, вычислим пропорции:
20 : 12,4 = 1,612…; 12,4 : 7,6 = 1,63…
Слайд 29
«Золотое сечение» в архитектурных сооружениях г.Алматы
Чтобы узнать, какие
архитектурные строения являются самыми примечательными, по мнению окружающих, мы
провели опрос среди учеников, предложив им на выбор двенадцать известных зданий нашего города.
Слайд 30
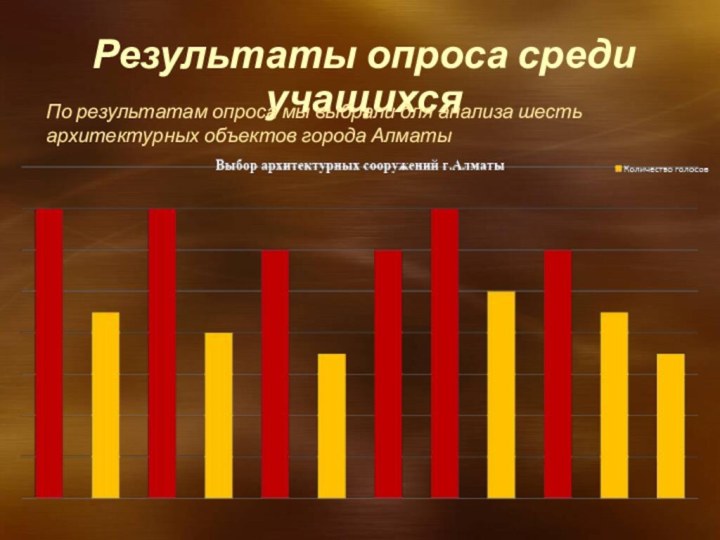
Результаты опроса среди учащихся
По результатам опроса мы выбрали
для анализа шесть архитектурных объектов города Алматы
Слайд 31
Свято-Вознесенский кафедральный собор
Главная достопримеча-тельность парка 28 гвардейцев-панфиловцев.
Уникальное
по инженерной конструкции сооружение высотой в 56 метров, построенное
в 1904 году без единого гвоздя из голубой тяньшаньской ели по проекту архитектора А.П. Зенкова.
Мы определили следующие пропорции:
а:а1:а2:а3:а4=1,618
Слайд 32
б:б1:б2:б3=1,618
Здание Государственного академического театра оперы и балета имени
Абая
Яркий пример конструктивизма, совет- ского авангардистского стиля, получившего развитие
в 1920–1930-х годах; характеризуется строгостью, геометриз- мом, лаконичностью форм и монолитностью внешнего облика.
Слайд 33
Казахстанско-Британский технический университет
Здание Бывшего Дома правительства Казахской ССР
– 5-этажное здание,
прямоугольное в плане,
поставленное на высокий
постамент.
Построено в стиле конструктивизма.
Строительство завершено в 1957 г.
1972 г. произведена реконструкция здания – были пристроеы два крыла.
Слайд 34
Центральный Государственный музей Республики Казахстан
Современное здание музея было
построено в 1985 г. по проекту архитекторов Ю.Ратушного, З.Мустафиной и Б.Рзагалиева.
Слайд 35
Парк имени первого президента
Главный вход в парк представлен
полукруглой аркадой. Архитектурно-композиционное решение входной группы основано на сочетании
декоративной колоннады, вынесенной на верхнюю отметку рельефа и полуподземного объема помещений общественного и технического назначения.
e:e1:e2:e3:e4:e5:e6=1,618
Главная идея парка – соединение уникального природного ландшафта Алматы и научных достижений ХХI века.
Слайд 36
Центральная мечеть
Главная городская мечеть Алматы была открыта в
1999 году, на сегодня, это монументальное сооружение является одним
из современных грандиозных памятников в Казахстане.
Слайд 37
Проект детской игровой площадки «Құлыншақ».
В проектировании детской игровой
площадки мы использовали результаты нашего исследования по решению простых
математических задач в строительном деле и применению пропорций «Золотого сечения».
Слайд 38
Основные этапы работы над проектом
Сбор и анализ информации
о требованиях к проектируемому объекту, изучение аналогов.
Разработка концепции будущей
площадки.
Определение формы и размеров детской площадки.
Ограждение участка и разбивка территории детской площадки на игровые зоны.
Выбор игровых элементов детской площадки и места их расположения. Расчеты занимаемой площади, зоны безопасности, стоимости и т.д.
Разработка схем и чертежей общего плана площадки и игровых элементов.
Расчет общей стоимости расходных материалов для детской площадки.
Слайд 39
Детская площадка — место, предназначенное для игры детей,
преимущественно дошкольного возраста, на котором расположены элементы детского уличного
игрового оборудования с целью организации содержательного досуга.
Основная концепция проекта детской игровой площадки:
наиболее эффективное конструирование и расположение элементов игровой площадки с использованием пропорций «Золотого сечения» при минимальных затратах на его строительство.
Тематическое оформление: использование элементов казахской национальной культуры.
Слайд 40
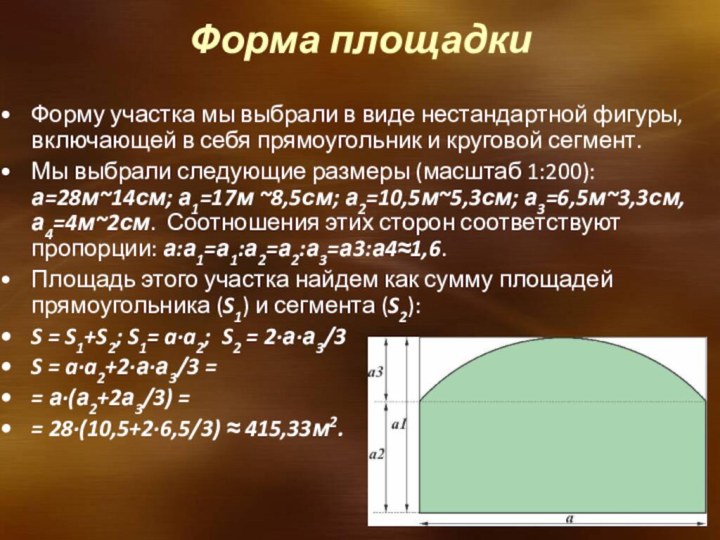
Форма площадки
Форму участка мы выбрали в виде нестандартной
фигуры, включающей в себя прямоугольник и круговой сегмент.
Мы
выбрали следующие размеры (масштаб 1:200): а=28м~14см; а1=17м ~8,5см; а2=10,5м~5,3см; а3=6,5м~3,3см, а4=4м~2см. Соотношения этих сторон соответствуют пропорции: а:а1=а1:а2=а2:а3=а3:а4≈1,6.
Площадь этого участка найдем как сумму площадей прямоугольника (S1) и сегмента (S2):
S = S1+S2; S1= a·a2; S2 = 2·а·а3/3
S = a·a2+2·а·а3/3 =
= а·(а2+2а3/3) =
= 28·(10,5+2·6,5/3) ≈ 415,33м2.
Слайд 41
Деление участка на зоны
Также по принципу «Золотого сечения»
мы поделили площадку на три части:
I – для младшей
возрастной группы,
II – для средней,
III – общая зона отдыха.
IV – в центре расположена беседка в виде юрты.
Перед обустройством детской площадки поверхность должна быть выровнена по максимуму. В нашем проекте площадка находится на готовом участке, засеянном травой.
Слайд 42
Установка ограждения
Необходимо установить ограждение по периметру и частично
обозначить границы зон . Можно установить готовое металлическое (или
деревянное) ограждение или высадить кустарники.
Найдем периметр этой нестандартной фигуры как сумму периметра прямоугольника без одной стороны и длины дуги.
P = P1 + L – a4 + а3 + 2·а4 = P1 + L + а3 + а4; P1 = 2·a2 + a = 21+28 = 49м; L = 2·15,4 + 0,93 = 31,73м; P = 49 + 31,73 + 6,5 + 4= 91,23 ≈ 91 м.
В Казахстане можно посадить кустарники для живой изгороди за 2000 тг на один квадратный метр. Примерная стоимость живой изгороди: 91 · 2000 = 182000тг.
Простое металлическое ограждение (высота 0,5 м, длина 2,5 м) стоит 9200 тг. Посчитаем какое количество таких ограждений нам понадобится: 91:2,5=36,4 ≈ 37 (округляем с избытком) , т.е. надо закупить 37 штук. Определим стоимость: 37 · 9200 = 340400 тг
Простое сравнение показывает, что выгоднее высадить живую изгородь.
Слайд 43
Для обозначения границ трех зон также применим использованные
автомобильные покрышки, наполовину вкопанные в землю. Это экономически выгодный
вариант, так как не требует затрат. Выступающую часть покрышек надо покрасить яркими экологически чистыми красками.
Определим количество краски, необходимое для покраски выступающей части автомобильных шин. Возьмем средние размеры: А=20см=0,2м (ширина профиля шины); H=12см=0,12м (высота профиля шины); D=63см=0,63м (наружный диаметр шины) R = 39см = 0,39м (посадочный диаметр). Тогда площадь поверхности половины шины равна: Sш = S1 + S2, где S1 площадь наружной поверхности, S2 площадь боковых поверхностей.
S1 = А·D·π/2 = 0,2·0,63·3,14/2 ≈ 0,2м2;
S2 = π·(D/2)2 - π·(R/2)2 = π/4·(D2-R2) = 3,14/4·(0,632-0,392) ≈ 0,19м2;
Sш = 0,2+0,19 ≈ 0,4м2.
Для 18 покрышек общая площадь для покраски составит S=9·0,4=3,6м2.
Для прочности окраски лучше всего покрасить покрышки в два слоя. Если расход краски Е=0,07кг/м2, то понадобится K=2·S·E=2·0,07·3,6≈0,5кг
Слайд 44
Игровые комплексы
На игровой площадке младшей группы (I) расположим
песочницу, горку с домиком, качель-балансир «Лошадки» и одноместные качели.
На игровой площадке средней группы (II) – турники трех видов и комплекс из трех видов качелей.
В зоне отдыха расположена беседка. Для отдыха на площадке также разместим 8 парковых скамеек со спинками. Можно установить небольшие скульптуры жеребенка и верблюжонка.
Слайд 45
Заключение
Анализируя все вышеизложенное можно еще раз подивиться грандиозности
процесса познания мира, открытием все новых его закономерностей и
сделать вывод: математика играет очень важную роль в строительстве и архитектуре.
Слайд 46
Расчет массы песка для песочницы
Рассчитаем массу песка, необходимого
для заполнения песочницы, а для этого нужно знать объем
песочницы. Заполнять будем на 2/3 от высоты бортика. Песочница имеет форму восьмиугольной призмы, поэтому ее объем вычисляем по формуле Vп = Sосн·h, где Sосн – площадь основания, h=2H/3 – высота наполнения бортика.
Основание песочницы – правильный восьмиугольник. Нам известны радиус описанной окружности R=D/2=1,5м и угол α=360º:8=45º. Площадь правильного восьмиугольника найдем как сумму площадей треугольников: S=8·S∆ABC.
S∆ABC =(1/2) ·AC·BC·sinα =(1/2) ·R2· sin45º = (√2 R2) /4≈ (1,4 ·1,52)/4 ≈ 0,788м2, тогда Sосн = 8 · S∆ABC = 8 · 0,788 ≈ 6,3м2.
Объём песочницы: V = Sосн·h = 6,3·0,2 = 1,26м3.
Теперь вычислим массу песка: mп=Vп · ρп=1,26м3 · 1500кг/м3=1890 кг ≈ 1,9т
Слайд 47
Беседка
Беседка, стилизованная под казахскую юрту, расположена в зоне
отдыха. В основании беседки лежит правильный восьмиугольник. На схеме
указаны размеры беседки в прямой проекции, а=4м, а1=2,47м, а2=1,53м, а3=0,94м, а4=0,58м. Здесь использованы пропорции «Золотого сечения»: а:а1=а1:а2=а2:а3=а3:а4=а4:а5=1,618…
Беседку можно украсить казахским национальным орнаментом, внутри беседки расположим по периметру лавки и посередине круглый стол.






















































![Конспект ООД по речевой деятельности. Тема: Звуки [м – м’] и буква М м план-конспект занятия по математике (подготовительная группа)](/img/tmb/8/743938/19612a42739b622212c7686000483545-210x.jpg)



















