Презентация на тему Применение информационных технологий при подготовке к ОГЭ и ГИА

массовых способов и приемов обработки информации во всех видах

человеческой деятельности с использованием современных средств связи, полиграфии, вычислительной техники и программного обеспечения.

Если при этом используются телекоммуникации, то появляется термин

Информационные
технологии
(ИТ)

Информационные
образовательные
технологии
(ИОТ)

все технологии в сфере образования, использующие специальные технические информационные средства для достижения педагогических целей.

С позиций информационного подхода любая педагогическая технология может быть названа информационной, так как сущность процесса обучения составляет движение и преобразование информации.

Когда компьютеры стали использовать
в образовании, появился термин

«новые
информационные
технологии»
(НИТ)

«информационно-
коммуникационные
технологии»
(ИКТ)

увиденного материала
½ часть услышанного и увиденного одновременно материала
¾ материала,

если ко всему прочему ученик вовлечён в активные действия в процессе обучения

учителя
с точки зрения ИКТ?

Разумеется, учитель должен:

уметь работать на компьютере;

должен иметь к нему неограниченный доступ;

уметь применять его в своей профессиональной
деятельности.

Информационные технологии

на уроках математики

«дружелюбность».
Компьютер позволяет усилить мотивацию учения учащегося.
1) С помощью обучающих

программ ученик может моделировать реальные процессы, а значит – видеть причины и следствия, понимать их смысл.

2) Интерес создаётся разнообразием и красочностью информации.

3) Появляется возможность устранить одну из важнейших причин отрицательного отношения к учёбе – неуспех. Ученик получает возможность довести решение любой задачи до конца, опираясь на необходимую помощь.

4) Раскрывается практическая значимость изучаемого материала, предоставляется возможность испробовать умственные силы.

5) Программное обеспечение в целом создаёт общий игровой фон общения человека с машиной.

как обучающего средства.
- 0% времени урока – обыкновенный урок,
-

100% времени урока – по существу, урока нет, есть компьютерное обучение.

- частичное использование – компьютерный урок,

Интенсивность использования компьютера:

с главной целью.
2) Отбираются наиболее эффективные средства из резервов

компьютерного обеспечения.
3) Рассматривается целесообразность их применения в сравнении с традиционными средствами.
4) Отобранные материалы оцениваются по времени, не превышающем санитарные нормы.
5) Составляется поминутный план урока.
6) При необходимости проводится поиск информации.
7) Составляется презентационная программа.
8) Предусматривается поэтапная и результирующая диагностика поставленных целей.

Этапы планирования компьютерного урока

самопроверки.
Повышение интереса учащихся к предмету.
Индивидуализированное обучение, учитывающее индивидуальные особенности

памяти, восприятия, мышления.
Расширение набора применяемых учебных задач.

Актуальность для урока с применением ИКТ

компакт-дисках
Компьютерные учебники
Презентации
Программы
Интернет

различную справочную информацию

математические построения, измерения и вычисления;
разработки уроков, задачники, учебники,

справочники; видеофрагменты, показывающие различные математические построения;
могут использоваться на отдельной части урока; и как систематизация учебного материала для подготовки учащихся к ЕГЭ.

не отвечать тем задачам, которые учитель ставит на уроке.
Большой

объем информации (информация не разбита на подразделы).
Нет навыков работы с данной программой (требуется время для обучения).
Сложная установка приложения с диска.
Сложность работы с компьютером, психологический фактор.

ходом урока.
Могут использоваться как на протяжении всего урока, так

и на отдельной его части.
Способствуют развитию интереса учащихся к предмету.
Позволяют вставлять мультимедиа объекты (видеофильмы, музыку, речь, графики и т д.).
Позволяют выиграть в оформлении урока.
Экономия времени урока.

этапах урока:

абсцисс
Ось OY – ось ординат
М(х; у)
Координаты
точки М
Ордината точки

М

Начало координат

Абсцисса точки М

I I I

I I

I V

I

М2(х2; у2)

М3(х3; у3)

М1(х1; у1)

Урок по теме: «Координатная плоскость»

при объяснении нового материала;

a=3,7 b= -5 c=1
2) a= -1 b=0

c=0
3) a=2,1 b=2 c= -2/3
4) a=7 b=0 c= -13
5) a=3 b=12 c= -1
6) a=1 b=3 c= -10
7) a=1/7 b= -3 c=0

Задание:

Ответы:

1) 3,7х2-5х+1=0,
2) -х2=0
3) 2,1х2-2/3+2х=0,
4) 7х2-13=0
5) х23+12х-1=0,
6) -10+3х+х2=0.
7) х2/7-3х=0.

Закрепление изучаемого материала

панель, работающая в комплексе с компьютером и проектором. ИД

в совокупности с персональным компьютером дает новые возможности образовательному процессу. К компьютеру, а, следовательно, и к интерактивной доске, может быть подключено любое дополнительное цифровое оборудование: цифровой фотоаппарат или видеокамера (со всеми отображенными материалами можно работать прямо во время урока).

Электронная
интерактивная доска
( ИД)

Вид панели доски

звуки, видео и т.д. можно найти во всемирной сети

Интернет.

Интернет.

Интернет

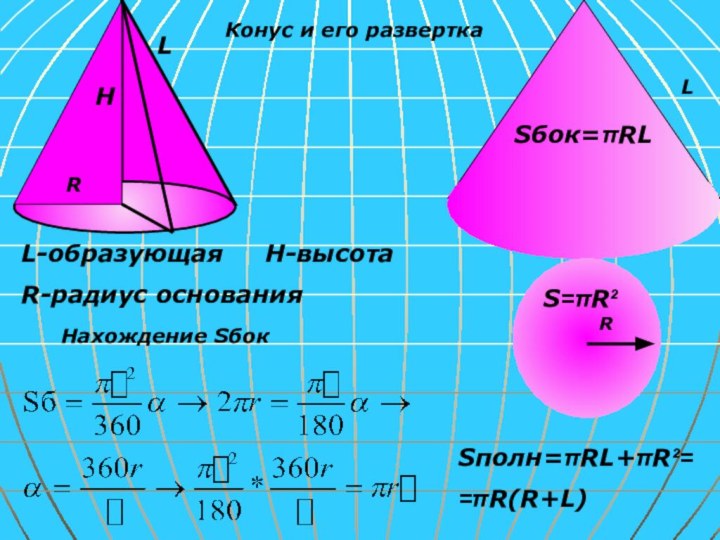
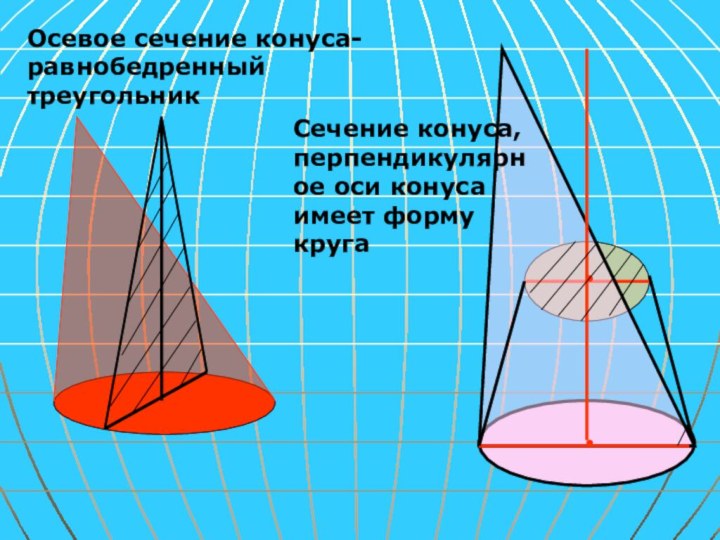
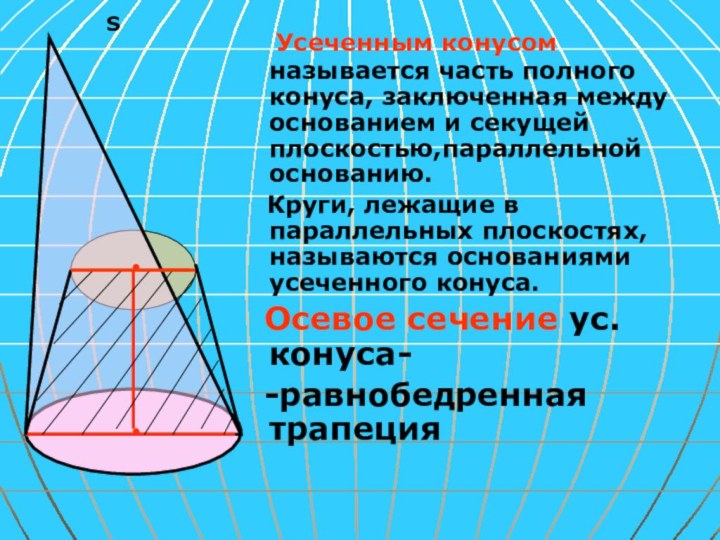
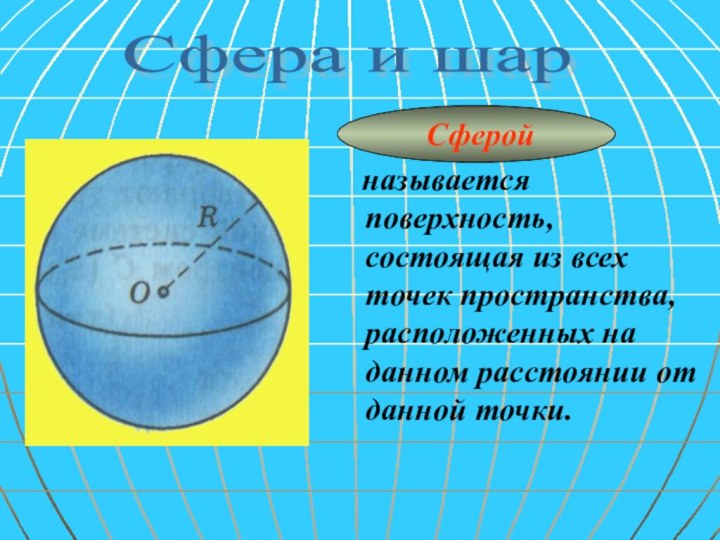
и образование
http://www.math.ru Московский центр непрерывного математического образования (МЦНМО)
http://www.mccme.ru Allmath.ru

- вся математика в одном месте
http://www.allmath.ru EqWorld: Мир математических уравнений
http://eqworld.ipmnet.ru Exponenta.ru: образовательный математический сайт
http://www.exponenta.ru Вся элементарная математика: Средняя математическая интернет-школа
http://www.bymath.net Геометрический портал
http://www.neive.by.ru/index.html Графики функций
http://graphfunk.narod.ru Дидактические материалы по информатике и математике
http://comp-science.narod.ru Дискретная математика: алгоритмы (проект Computer Algorithm Tutor)
http://rain.ifmo.ru/cat/ ЕГЭ по математике: подготовка к тестированию
http://www.uztest.ru Задачи по геометрии: информационно-поисковая система
http://zadachi.mccme.ru Задачник для подготовки к олимпиадам по математике
http://tasks.ceemat.ru Занимательная математика - школьникам
http://www.math-on-line.com Интернет-проект «Задачи»
http://www.problems.ru Математические этюды
http://www.etudes.ru Математика on-line: справочная информация в помощь студенту
http://www.mathem.h1.ru Математика в помощь школьнику и студенту (тесты по математике online)
http://www.mathtest.ru Математика для поступающих в вузы
http://www.matematika.agava.ru Математика: Консультационный центр преподавателей и выпускников МГУ
http://school.msu.ru Математика и программирование
http://www.mathprog.narod.ru Математические олимпиады и олимпиадные задачи
http://www.zaba.ru Международный математический конкурс «Кенгуру»
http://www.kenguru.sp.ru Методика преподавания математики
http://methmath.chat.ru Московская математическая олимпиада школьников
http://olympiads.mccme.ru/mmo/ Решебник.Ru: Высшая математика и эконометрика - задачи, решения
http://www.reshebnik.ru Сайт элементарной математики
http://www.mathnet.spb.ru Турнир городов - Международная математическая олимпиада для школьников
 

 
Федеральные образовательные порталы
http://www.edu.ru/
Центральный образовательный портал. Содержит нормативные документы Министерства образования и науки, стандарты, информацию о проведении экспериментов.
http://pedsovet.org
Всероссийский Интернет-педсовет. В разделе «Библиотека» имеются рубрики «Методика и опыт», «Педсовет», «Технологии».
http://www.fipi.ru/
Федеральный институт педагогических измерений. Содержит контрольные измерительные материалы, репетиционное тестирование, федеральный банк тестовых заданий.
http://www.ege.edu.ru/
Портал информационной поддержки Единого государственного экзамена.
 
Методические разработки
http://www.math.ru/
Интернет-поддержка учителей математики. Содержит электронные книги, видеолекции, материалы для уроков.
http://www.mccme.ru/
Московский центр непрерывного математического образования. Содержит варианты конкурсов для учителей и учащихся, математических олимпиад, множество задач.
http://www.it-n.ru/
Сеть творческих учителей. Содержит: библиотеку готовых учебных проектов с применением ИКТ; библиотеку методик проведения уроков с использованием разнообразных электронных ресурсов; руководства и полезные советы по использованию программного обеспечения в учебном процессе.
http://www.problems.ru/
База данных задач по всем темам школьной математики. Содержит задачи различных рубрик и степеней сложности с решением.
http://www.som.fsio.ru/
Сетевое объединение методистов. Содержит в разделе «Математика» статьи, методические разработки уроков, сценарии праздников, внеклассные мероприятия.
http://www.som.fsio.ru/
Образовательный математический сайт. Содержит материалы по работе с математическими пакетами Mathcad, MATLAB, Mathematica, Maple и др. Методические разработки, примеры решения задач, выполненные с использованием математических пакетов.

Сайты, в помощь
учителю математики

наглядности
Возможность организации проектной деятельности учащихся по созданию учебных программ
Внимание

логике изложения материала
Облегчение труда учителя на уроке

превращается в чрезвычайное событие, что мешает восприятию и усвоению

материала.
2) Если компьютер используется слишком часто, то к нему теряется интерес.
3) Использование компьютера не должно длиться на уроке подряд более 10-15 минут (начальная школа),
20-25 минут (средняя ступень),
30 минут (старшая ступень).
Общее суммарное время работы в день:
50, 120, 200 минут соответственно.

Техника безопасности

в жизнь свои идеи и задумки в виде проектов.

Мы и вам предлагаем познакомиться с этой удивительной программой, с ее инструментами, приемами и способами построения различных фигур, с теми возможностями, которые программа в себе содержит.

двигать объекты.
Также существуют еще два вида курсоров- расширяющий и

поворачивающий:

Изменяют курсор так: нажимают на кнопку «курсор» и не отпускают.
Появятся все виды курсоров справа от кнопки:
Не отпуская нажатие мы переносим курсор на
один из предложенных. Останавливаем на нужном и прекращаем нажатие.

- ставит точки в любом

месте чертежа.

Этот инструмент очень прост. Можно поставить точку в любом месте чертежа, независимо от уже построенных изображений или на них
При этом если точка начинает накладываться на некоторый объектом, то этот объект выделяется синим цветом:

- рисует окружности везде или на объектах.
Когда

мы рисуем окружность, то мы должны поставить 2 точки: ее центр и одну из точек самой окружности, то есть, фактически, поставить начало и конец одного из радиусов окружности.
Мы можем поставить эти точки где угодно и как угодно: строго на пересечении объектов, или на одном из них, или в стороне от уже нарисованных фигур.
Когда мы выбираем, куда поставить одну из вышеуказанных точек, и попадаем на какой – нибудь объект, то происходит то же, что и с простой точкой – этот объект выделяется.

Инструменты «Живой геометрии»:

- рисует отрезки прямой

в любом месте и
произвольной длины

Работает этот инструмент так же как инструмент «Окружность». Только теперь мы отмечаем точки начала и конца отрезка. У инструмента «прямая», также, как и у инструмента «курсор», есть различные вариации: стрелка и указатель длины.

Инструменты «Живой геометрии»:

- дает возможность надписать имя объекта,

или любой текст.

Здесь нет ничего проще:
выделяете объект и пишете его имя,
или
выделяете место на экране и пишете свой комментарий.

Инструменты «Живой геометрии»:

- дает возможность создавать и

использовать созданные тобой
объекты.

На мой взгляд, это самый сложный инструмент.
Объект, который мы используем достаточно часто, можно сохранить, как свои личный инструмент, и потом использовать его аналогично уже рассмотренным инструментам.
Мы просто выделяем все, что хотим иметь в качестве инструмента, нажимаем и удерживаем кнопку «инструмент» и таким образом создаем необходимый нам объект, называя его каким-либо именем .
Чтобы использовать созданный объект, выбираем его из списка «нового инструмента» и строим, как одно целое. Количество инструментов, которые можно таким образом создать, не ограничено.

Инструменты «Живой геометрии»:

все ее девять функций:
Файл, Редактор, Вид, Построения,

Преобразования, Измерения, Графики, Окно и Справка.

начать создавать чертеж с чистого листа
- открыть ранее созданный проект или чертеж

сохранить только что сделанный чертеж
сохранить чертеж с самостоятельным выбором места сохранения
- закрыть проект, который создается или редактируется

работать с последовательностью страниц и с самими страницами непосредственно

настроить работу принтера с программой и опции печати
предварительно просмотреть вид проекта перед печатью
войти в мастер печати

закрыть программу «Живая геометрия»

функция Файл позволяет :

функция Файл позволяет :

действие
вырезать выделенные объекты
копировать объекты, которые были

выделены
вставить рисунок (скриншот) рабочего стола
удалить вставленный или ненужный объект

- создавать кнопки анимации, исчезновения и др.

выделить все объекты на странице
показать то, на чем строился выделенный потомок
показать всех потомков выделенного объекта

создать или удалить зависимости
изменить значения определения функции

- определить свойства выделенного объекта

- настроить саму программу ( например:
установить единицы измерения углов и расстояний, цвет всех объектов, которые можно построить, параметры возникновения и исчезновения объектов с их цветами), а также настроить текст (разрешить или запретить устанавливать компьютеру имена всех точек, объектов, участвовавших в измерениях; настроить панель атрибутов текста и указать случаи, когда компьютеру надо ее выводить на экран).

Редактор

функция позволяет: :

линий
выбирать вид текста и его размеры
скрывать выделенные

объекты исчезнут, но не удалять их
показывать все скрытые объекты

- показывать имена всех объектов

рисовать траекторию движения объекта
стирать все следы от всех объектов

начать движение выделенных объектов произвольным образом
увеличивать скорость движения объектов
уменьшать скорость анимации
останавливать движение всех объектов

работать с панелью атрибутов текста
работать с панелью управления анимацией
спрятать все панели инструментов

функция позволяет :

кнопку для каждого простого (основного) объекта, такого как прямая,

биссектриса и др.

Преобразования:

позволяет использовать такие преобразования плоскости, как гомотетия, параллельный перенос, отражение и поворот на угол.

Измерения:

предоставляет возможность измерять расстояния между точками, длины отрезков и радиусы окружностей, углы и площади, а также отношение величин и углы наклона. Здесь также предложены действия на координатной плоскости (работа с абсциссами и ординатами точек).

Графики:

дает возможность работать с графиками. Здесь содержится большой список стандартных функций, есть таблицы значений. Можно самостоятельно задать функцию и построить ее график. При этом здесь есть возможность определять координаты точек, менять толщину, цвет и вид линий.

Названия остальных функций говорят сами за себя:

Названия остальных функций говорят сами за себя:

то их можно расположить каскадом или мозаикой. Или же

можно переключиться на один из данных проектов, и при этом в нижнем окошке клавиши, в списке всех открытых презентаций возле выбранной появится галочка (см. слева). Переключаются следующим образом:

Возле кнопок закрывания и свертывания окна «Живой геометрии», а точнее под ними вы увидите такие же:

Это кнопки свертывания и закрывания окна непосредственно самой презентации.

Справка:

На мой взгляд, совершенно ненужная кнопка. Если вы нажмете на нее, то высветится реклама – заплатка программы «Живой геометрии». Такая же высвечивается при запуске программы.

Традиционные функции :

может встретить начинающий
работу с «Живой геометрией» и советы

что и как лучше делать.

1) Существуют кнопки: анимация и презентация. Если их правильно сочетать, то можно получить такие же модели с кнопками, как на страницах 5 – 6 моей «Демонстрации возможностей в самой программе». Например, есть окружность с точкой. Если выделить точку и сделать кнопку ее анимации, а затем выделить последнюю и сделать кнопку презентации, то с помощью презентации мы можем назначить время действия анимации и объединить в одну кнопку несколько. Таким образом я смог сделать вращательное движение, которое длится некоторое времени.
2) Выделив несколько точек по периметру фигуры и нажав в меню «построения» и в этом подменю «внутренность» можете раскрасить внутреннюю область фигуры в определенный цвет.
3) Не двигайте колесиком мышки резко вверх – вниз – программа в 99% случаев зависает!!!
4) Есть огромное преимущество программы – она запоминает примерно 1000 ваших действий! То есть отменить можно не несколько предыдущих действий, как в Power Point и Paint , а все действия с начала работы!!!

интересного,
узнаете много нового и
откроете для себя

M
a
M
Построение:
1. Провести перпендикуляр MP к прямой a
P
2.

Отложить на прямой MP отрезок PM1, равный отрезку MP

M1

Итак, осевая симметрия представляет собой отражение плоскости на себя

Отложить на прямой MP отрезок PM1, равный отрезку MP
P
P
3.

Аналогично с точками N и N1

Итак, движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.

окружность, и из каждой ее точки восстановить перпендикуляр до

пересечения со второй плоскостью, то получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров, это тело называется цилиндром.

1.Как можно получить цилиндр

Круги, лежащие в параллельных плоскостях, называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей оснований –называются образующими цилиндра.

из его сторон

основания
4
Радиусом цилиндра называется радиус его основания.

боковую (цилиндрическую) поверхность цилиндра.
1
2
3
4
4
2. Образующие
Поверхность, состоящая из образующих, называется

боковой поверхностью цилиндра.

имеет форму прямоугольника и называется «осевым»
Сечение плоскостью, перпендикулярной к

оси или параллельное основаниям, является кругом.

β

α

β

о

о1

γ

3.Сечения цилиндра

Сечение , параллельное оси цилиндра-прямоугольник

проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения,

содержащей эту образующую

Н и С, где Н – высота цилиндра, а

С – длина окружности основания.

н

С=2πR

S=πR²

S=πR²

катетов, тогда второй катет описывает окружность.
Полученная при вращении фигура

называется конусом.

3. Гипотенуза данного треугольника-образующая конуса

4.Катет, вокруг которого вращается треугольник – ось конуса,
Второй катет- радиус описываемой окружности основания

Sбок
Sполн=πRL+πR²=
=πR(R+L)

имеет форму круга

заключенная между основанием и секущей плоскостью,параллельной основанию.

Круги, лежащие в параллельных плоскостях, называются основаниями усеченного конуса.
Осевое сечение ус. конуса-
-равнобедренная трапеция

полного конуса, заключенная между основаниями. Высотой усеченного конуса называется

расстояние между основаниями.

ℓ

h

R

r

Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

называется поверхность, состоящая из всех точек пространства, расположенных

на данном расстоянии от данной точки.

Сфера и шар

ОДНОЙ ОБЩЕЙ ТОЧКИ
ПЛОСКОСТЬ ПЕРЕСЕКАЕТ ШАР
о
о
о
С(0;0;d)
С(0;0;d)
С(0;0;d)
R
d
Взаимное расположение сферы и плоскости

называется касательной к сфере
Радиус сферы, проведенный к точке касания

сферы и плоскости перпендикулярен к касательной плоскости.
ОА┴α

А′

ОА=R, если ОА┴α, то любая другая ОА′- наклонная, а любая наклонная больше , чем ОА, т.е. условие не выполняется( ОА′>R)

Обратная теорема : Если ОА┴α, α-касательная плоскость

Т.к. перпендикуляр и плоскость имеют одну общую точку, то α- касательная плоскость

двумя параллельными секущими плоскостями.

него какой - нибудь плоскостью.

сектора с углом, меньшим 900, вокруг прямой, содержащей один

из ограничивающих круговой сектор радиусов.

соединяющий концы этих радиусов

лежащие углы равны, то прямые параллельны.
460
460
a
b
aIIb
c
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ.

соответственные углы равны, то прямые
параллельны.
420
a
b
aIIb
c

пересечении двух прямых секущей сумма односторонних углов равна 1800,

прямые параллельны.

b

а

Если

то

1

2

c

сумма
односторонних углов равна 1800, то прямые

параллельны.

420

1380

a

b

aIIb

c

b
a
d
c
1
3
2
4
6
5

прямых с помощью

рейсшины.

имеют общих точек.
аIIβ

а
β

какой-нибудь прямой, лежащей в этой плоскости, то она параллельна

данной плоскости.

a

b

β

Следствие из теоремы.
1°. Если плоскость проходит через данную прямую,

параллельную другой плоскости, и пересекает эту плоскость, то линии пересечения плоскостей параллельна данной плоскости.

β

из теоремы.

2°. Если одна из двух параллельных прямых параллельна

данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

двум прямым другой плоскости, то эти плоскости параллельны.
α
β
a
b
a1
b1
α׀׀β

их пересечения параллельны.
α
β
γ
a
b
a׀׀b

у него все стороны и все углы равны.
Правильный треугольник
Квадрат
Правильный

шестиугольник

Правильный восьмиугольник

можно описать окружность и притом только одну.
О
R

многоугольник можно вписать окружность и притом только одну.
О
r

их серединах.
Следствие2. Центры окружностей вписанной в правильный многоугольник и

описанной около него совпадают. Эта точка называется центром правильного многоугольника.

О

R

r

Сторона правильного многоугольника:
Радиус вписанной окружности: