- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Числа Фибоначчи
Содержание
- 2. Последовательность Фибоначчи, известная всем по фильму "Код
- 3. Кто-то поместил пару кроликов в некоем замкнутом
- 4. В итоге получается такой ряд цифр: 1, 1,
- 5. Мы начинаем с двух квадратов первого размера.
- 6. Спираль АрхимедаЕсли мы проведём плавную линий через
- 7. Ничего не напоминает?
- 9. Броколи романеско:
- 12. Скачать презентацию
- 13. Похожие презентации
Последовательность Фибоначчи, известная всем по фильму "Код Да Винчи" - ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:


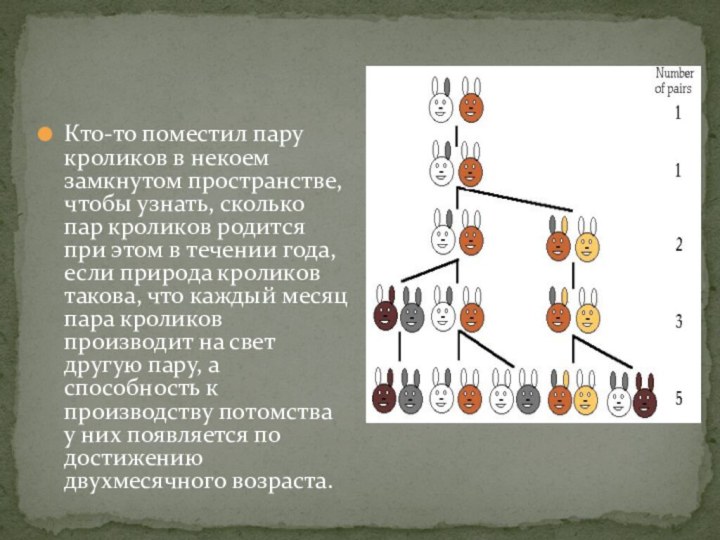








Слайд 3 Кто-то поместил пару кроликов в некоем замкнутом пространстве,
чтобы узнать, сколько пар кроликов родится при этом в
течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.Слайд 4 В итоге получается такой ряд цифр: 1, 1, 2,
3, 5, 8, 13, 21, 34, 55, 89, 144,
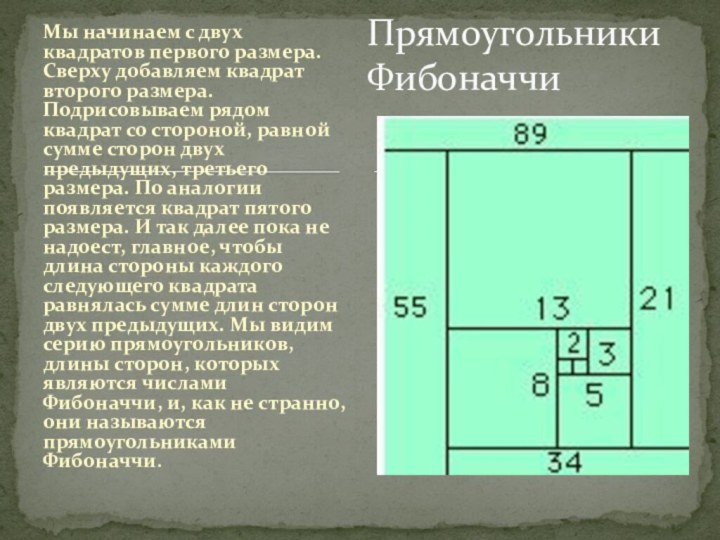
где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Его можно продолжать бесконечно долго. Его суть в том, что каждое следующее число является суммой двух предыдущих.Слайд 5 Мы начинаем с двух квадратов первого размера. Сверху
добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной,
равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.Прямоугольники Фибоначчи





























