Слайд 2
"В геометрии существует два сокровища - теорема Пифагора
и деление отрезка в крайнем и среднем отношении. Первое
можно сравнить с ценностью золота, второе можно назвать драгоценным камнем".
Иоганн Кеплер
Слайд 3
Пифагор ( 570—490 гг. до н. э.) —
древнегреческий философ,
Математик и мистик, создатель религиозно-философской школы
пифагорейцев.
Пифагор родился на острове Самос. Первым учителем Пифагора был Гермодамас. Он прививает своему ученику любовь к музыке и живописи, заставляет наизусть учить отрывки из «Илиады» и «Одиссеи».
Самос
Слайд 4
Родной остров Пифагор покинул в 18 лет,
затем много путешествовал и спустя несколько лет добрался до
Египта. Там он жил 22 года, после чего был вынужден уехать в Вавилон как пленник. В 525 до н. э персидский правитель Камбиз захватил Египет и Пифагору пришлось смириться с ролью раба. В Вавилоне он активно изучает науки, много общается со жрецами и возвращается на родной Самос только в 56-летнем возрасте. Пифагор остановился в Кротоне – греческой колонии, расположенной в Южной Италии. Постепенно ученики Пифагора создали организацию,которая весьма напоминала религиозный орден. В него входили только избранные. В Кротоне со временем данный орден практически захватил власть.
Слайд 5
В школе Пифагора впервые была выдвинута идея о
том, что Земля на самом деле является круглой. Естественно,
эта идея обществом
воспринята не была. Ряд идей, которые впоследствии произвели настоящую революцию в астрономии, были впервые озвучены именно Пифагором. В конце VI в. до н. э. начали расти антипифагорейские настроения, и в результате философ вынужден в колонию Метапонт. Здесь он прожил до самой смерти. В первом веке до нашей эры, во времена Цицерона, склеп Пифагора показывали в качестве одной из местных достопримечательностей.
Слайд 6
Теорема, названная его именем, является едва ли
не самой знаменитой теоремой геометрии, которую помнит каждый человек,
который когда-либо учился в средней школе. Теорема утверждает, что в прямоугольном треугольнике катеты a и b связаны с гипотенузой с следующим простым соотношением:
c2=a2+b2 .
a
b
с
Если дан нам треугольник И при том с прямым углом, То квадрат гипотенузы Мы всегда легко найдем: Катеты в квадрат возводим, Сумму степеней находим - И таким простым путем К результату мы придем.
Слайд 7
Одно из первых упоминаний теоремы Пифагора относится еще
к древнему Китаю: математическая книга Чу-пей (около 2400 г.
до н. э.). В этом сочинении так говорится о "пифагоровом треугольнике" со сторонами 3, 4 и 5: "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4". В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии "Лилавати" Бхаскары.
Фрагменты "Лилавати" Бхаскары и древнекитайского трактата Чжоу-би
Слайд 8
Крупнейший немецкий историк-математик Кантор считает, что теорема Пифагора
была известна египтянам около 2300г. до н.э., во времена
фараона Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5, которые назывались также "священными" или "египетскими", так как они широко использовались в египетской культуре.
"Священный" или "египетский" треугольник
Слайд 9
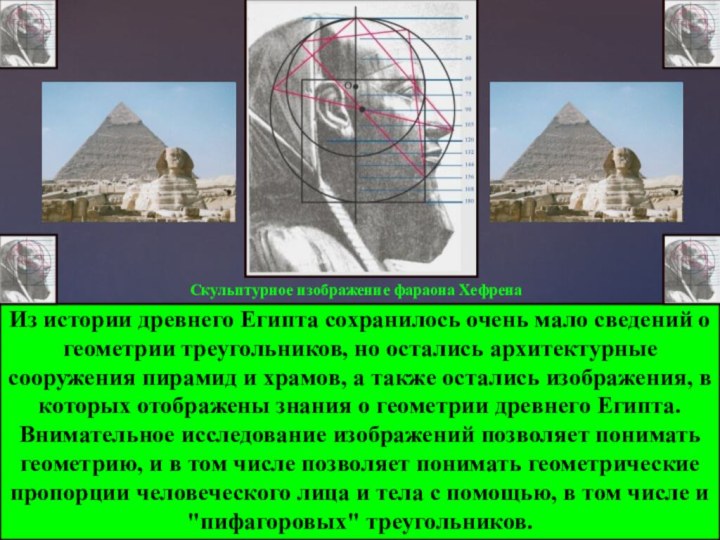
Из истории древнего Египта сохранилось очень мало сведений
о геометрии треугольников, но остались архитектурные сооружения пирамид и
храмов, а также остались изображения, в которых отображены знания о геометрии древнего Египта. Внимательное исследование изображений позволяет понимать геометрию, и в том числе позволяет понимать геометрические пропорции человеческого лица и тела с помощью, в том числе и "пифагоровых" треугольников.
Скульптурное изображение фараона Хефрена
Слайд 10
Несколько больше известно о теореме Пифагора у вавилонян.
В одном тексте, относимом ко времени Хаммурапи, т. е.
к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях. Всё это было им необходимо при астрономических наблюдениях, которые, по-видимому, главным образом и привели их к геометрическим знаниям.
Слайд 11
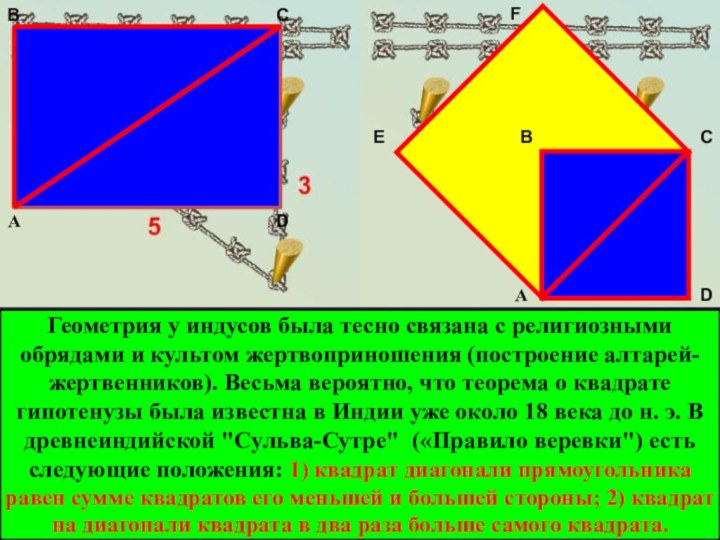
Геометрия у индусов была тесно связана с религиозными
обрядами и культом жертвоприношения (построение алтарей-жертвенников). Весьма вероятно, что
теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э. В древнеиндийской "Сульва-Сутре" («Правило веревки") есть следующие положения: 1) квадрат диагонали прямоугольника равен сумме квадратов его меньшей и большей стороны; 2) квадрат на диагонали квадрата в два раза больше самого квадрата.
А
B
C
D
А
B
C
D
E
F
Слайд 12
В настоящее время известно, что эта теорема не
была открыта Пифагором. Сегодня принято считать, что Пифагор дал
первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал".
Слайд 13
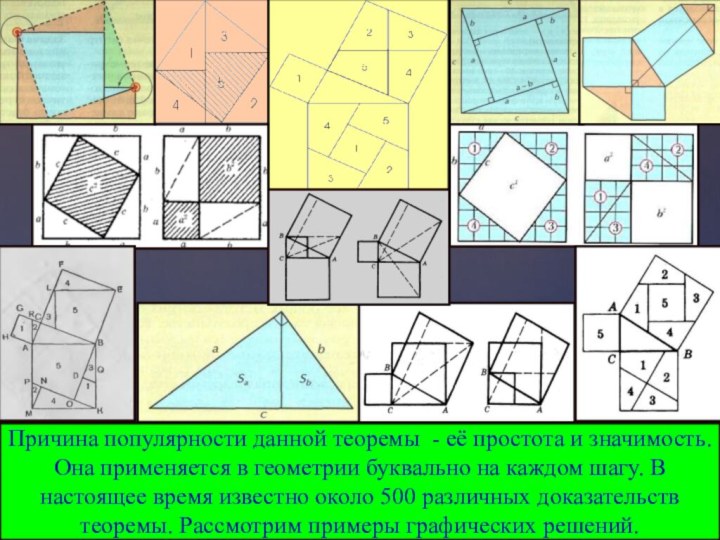
Причина популярности данной теоремы - её простота и
значимость. Она применяется в геометрии буквально на каждом шагу.
В настоящее время известно около 500 различных доказательств теоремы. Рассмотрим примеры графических решений.
Слайд 14
Рассмотрим алгебраический метод доказательства теоремы Пифагора из учебника
"Геометрия" (7-9классы)
Теорема Пифагора. В прямоугольном треугольнике
квадрат
гипотенузы равен сумме квадратов катетов.
Доказательство. Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой с (рис.1). Докажем, что с² = a² + b².
Достроим треугольник до квадрата со стороной a+b так, как показано на рис. 2.
Рис.1
Рис.2
Площадь S этого квадрата равна (a +b)². С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ ab, и квадрата со стороной с, поэтому
S = 4· ½ab + с² = 2ab + с². Таким образом,
(a +b)² = 2ab + с², откуда
с² = a² + b², и теорема доказана.
Слайд 15
Теорема Пифагора - одна из главных и, можно
сказать, самая главная теорема геометрии. Значение ее состоит в
том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна. Сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: "Квадрат гипотенузы равен сумме квадратов катетов".
Посмотрите на эти два квадрата, и все сразу становится ясно. Индусы к этому чертежу добавляли лишь одно слово: "Смотри!".
Слайд 16
Доказательство теоремы Пифагора учащиеся средних веков считали очень
трудным и называли его "Dons asinorum" - "ослиный мост",
или "elefuga" - "бегство убогих", так как некоторые "убогие" ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому "ослами", были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также "ветряной мельницей", составляли стихи вроде "Пифагоровы штаны на все стороны равны", рисовали карикатуры.
Слайд 17
Теорема используется в машиностроении; астрономии;
строительстве молниеотвода, крыш,
окон,
мобильных вышек; архитектуре.
На каком острове родился Пифагор?
А) Тасос, Б) Кротоне,
В) Самос, Г) Эвбея
Слайд 20
Ответ на задание №1
Пифагор родился на острове
Самос в 570 году до н. э.
.
Правильный ответ В)
Слайд 21
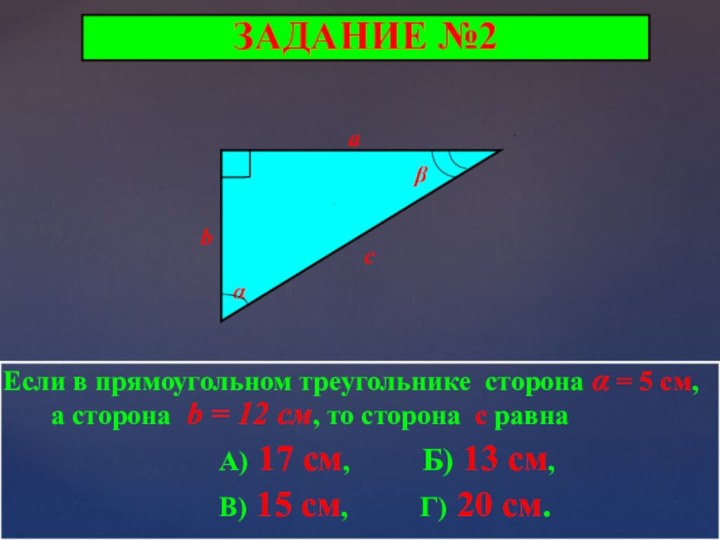
ЗАДАНИЕ №2
Если в прямоугольном треугольнике сторона α =
5 см, а сторона b = 12 cм, то
сторона с равна
А) 17 см, Б) 13 см,
В) 15 см, Г) 20 см.
Слайд 22
Ответ на задание №2
Сумма квадратов катетов равна квадрату гипотенузы. 5²+12²=25+144=169=13².
Правильный ответ Б)
Слайд 23
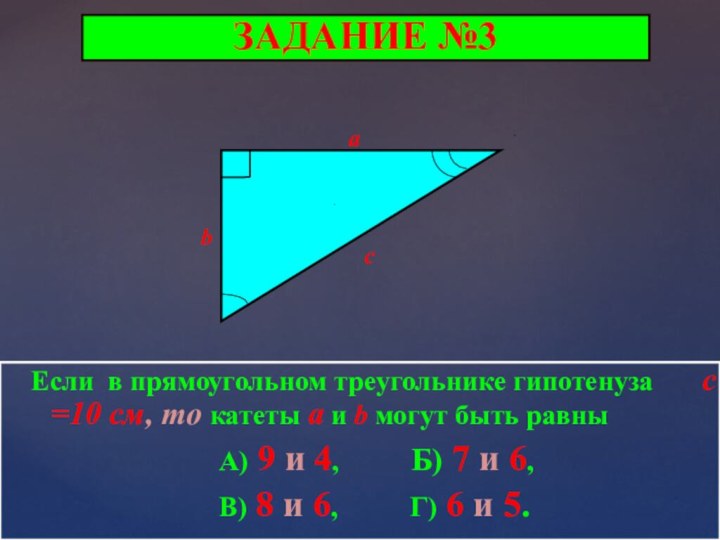
ЗАДАНИЕ №3
Если в прямоугольном треугольнике гипотенуза
с =10 см, то катеты a
и b могут быть равны
А) 9 и 4, Б) 7 и 6,
В) 8 и 6, Г) 6 и 5.
Слайд 24
Ответ на задание №3
По теореме Пифагора
с² = a² + b² = 8² + 6² = 100, откуда с = 10.
.
Правильный ответ В)
Слайд 25
ЗАДАНИЕ №4
Какой из треугольников
со сторонами
А) (1;1;√2), Б) (3;4;5),
В) (4;6;7), Г) (9;12;15)
не является "пифагоровым" треугольником?
Слайд 26
Ответ на задание №4
Действительно, 4² + 6²
= 52 ≠ 49 = 7². Стоит отметить, что
во времена Пифагора правильным был бы считался
и ответ А), так как были неизвестны
рациональные числа.
.
Правильный ответ В)
Слайд 27
ЗАДАНИЕ №5
В какой из этих
древних стран впервые
упоминаются условия теоремы Пифагора:
А) Китай, Б) Греция,
В) Египет, Г) Индия.
Слайд 28
Ответ на задание №5
Первые упоминания о теореме
Пифагора дошли до нас в древнекитайских трактатах, датированных
приблизительно 2400г.
Правильный ответ А)
Сформулируйте теорему,
обратную теореме Пифагора.
Слайд 30
Ответ на задание №6
Эта теорема звучит следующим образом:
"Если квадрат
одной стороны треугольника равен сумме квадратов
двух других сторон, то треугольник прямоугольный".
.
Слайд 31
Как знание теоремы Пифагора использовали
А) египтяне
1) для астрономических наблюдений Б)вавилоняне 2) для религиозных обрядов
В)индусы 3)для строительств
Слайд 32
.
Правильные ответы
А) - 3), Б) – 1),
В) – 2).
Слайд 33
Если вы дали правильные ответы на все
шесть заданий, можете смело требовать
пятерку по геометрии !!!
Если же ответили правильно на 3 задания или меньше, то еще раз пересмотрите презентацию и попробуйте разгадать кроссворд. Это повысит вашу оценку и самооценку. Успехов!
Слайд 35
По горизонтали:
1. Как называли египтяне треугольник со сторонами
3, 4, 5?
2. Имя древнегреческого математика, которому некоторые ученые
приписывают доказательство теоремы Пифагора.
3. Ученый, в честь которого названа теорема.
4. Страна, где впервые упоминается условие теоремы Пифагора.
5. Колония, где умер Пифагор.
6. Колония, где Пифагор создал свою школу.
7. Ученики этой эпохи рисовали карикатуры на чертежах, которые являлись доказательством теоремы Пифагора.
По вертикали:
1. Знание геометрии в этой стране люди использовали для постройки пирамид.
2. В прямоугольном треугольнике сумма квадратов 2 катетов равна квадрату…..
3. Город, в котором Пифагор перенимал знания геометрии у жрецов.
4. Вавилоняне изучали эту науку, используя знания о геометрии.
5. Этот народ использовал знание геометрии для строительства алтарей-жертвенников.