- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике к открытому уроку по теме Правильные многогранники
Содержание
- 2. ОпределениеМногогранник называется правильным, если:он выпуклый;все его грани являются равными правильными многоугольниками;в каждой его вершине сходится одинаковое число рёбер.
- 3. Немного историиПравильные многогранники известны с древнейших времён.
- 4. Каждая из шести сфер соответствовала одной из
- 5. Тетраэдр
- 6. Тетраэдры в техникеТетраэдр образует жёсткую, статически определимую
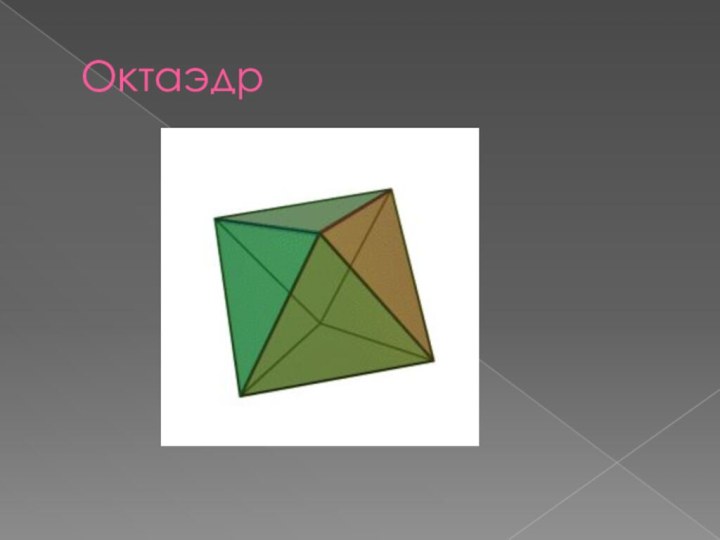
- 7. Октаэдр
- 8. Октаэдр в природе Многие природные кубические кристаллы имеют форму октаэдра.
- 9. Икосаэдр
- 10. История Евклид в предложении 16 книги XIII «Начал»
- 11. В мире Икосаэдр лучше всего из всех правильных
- 12. Додекаэдр
- 13. История Пожалуй, самый древний предмет в форме
- 14. Скачать презентацию
- 15. Похожие презентации
ОпределениеМногогранник называется правильным, если:он выпуклый;все его грани являются равными правильными многоугольниками;в каждой его вершине сходится одинаковое число рёбер.












Слайд 2
Определение
Многогранник называется правильным, если:
он выпуклый;
все его грани являются равными правильными
многоугольниками;
Слайд 3
Немного истории
Правильные многогранники известны с древнейших времён. Их
орнаментные модели можно найти на резных каменных шарах, созданных в
период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы (исключая Землю) и правильными многогранниками. В книге «Тайна мира», опубликованной в 1596 году, Кеплер изложил свою модель Солнечной системы. В ней пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер.
Слайд 4 Каждая из шести сфер соответствовала одной из планет
(Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну). Многогранники были расположены в следующем порядке (от внутреннего
к внешнему): октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб. Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками. Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера, — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников (тел Кеплера — Пуансо).
Слайд 6
Тетраэдры в технике
Тетраэдр образует жёсткую, статически определимую конструкцию.
Тетраэдр, выполненный из стержней, часто используется в качестве основы
для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр
Слайд 8
Октаэдр в природе
Многие природные кубические кристаллы имеют форму октаэдра. Это алмаз, хлорид натрия, перовскит, оливин, флюорит, шпинель.
Форму
октаэдра имеют межатомные пустоты (поры) в плотноупакованных структурах чистых
металлов (никеле, меди, магнии, титане, лантане и многих других) и ионных соединений (хлорид натрия, сфалерит, вюрцит и др.).
Слайд 10
История
Евклид в предложении 16 книги XIII «Начал» занимается построением
икосаэдра, получая сначала два правильных пятиугольника, лежащих в двух параллельных
плоскостях — из десяти его вершин, и затем — две оставшиеся противоположные друг другу вершины[2][3]:127-131. Папп Александрийский в «Математическом собрании» занимается построением икосаэдра, вписанного в данную сферу, попутно доказывая, что двенадцать его вершин лежат в четырех параллельных плоскостях, образуя в них четыре правильных треугольника
Слайд 11
В мире
Икосаэдр лучше всего из всех правильных многогранников подходит для
триангуляции сферы методом рекурсивного разбиения[6]. Поскольку он содержит наибольшее
среди них количество граней, искажение получающихся треугольников по отношению к правильным минимально.Икосаэдр применяется как игральная кость в настольных ролевых играх, и обозначается при этом d20 (dice — кости).
Тела в виде икосаэдра
Капсиды многих вирусов (например, бактериофаги, мимивирус).
Слайд 13
История
Пожалуй, самый древний предмет в форме додекаэдра был
найден в северной Италии, около Падуи, в конце XIX века, он
датируется 500 г. до н.э. и предположительно использовался этрусками в качестве игральной кости.Додекаэдр рассматривали в своих сочинениях древнегреческие учёные. Платон сопоставлял с правильными многогранниками различныеклассические стихии. О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца»[4]. Евклидв предложении 17 книги XIII «Начал» строит додекаэдр на рёбрах куба. Папп Александрийский в «Математическом собрании» занимается построением додекаэдра, вписанного в данную сферу, попутно доказывая, что вершины додекаэдра лежат в параллельных плоскостях
На территории нескольких европейских стран найдено множество предметов, называемых римскими додекаэдрами, относящихся ко II—III вв. н.э., назначение которых не совсем понятно.