Презентация на тему по математике к уроку на тему Длина окружности

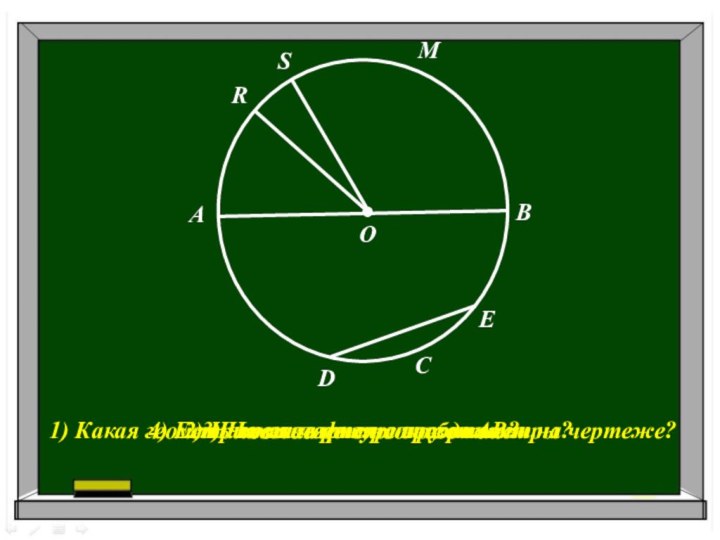
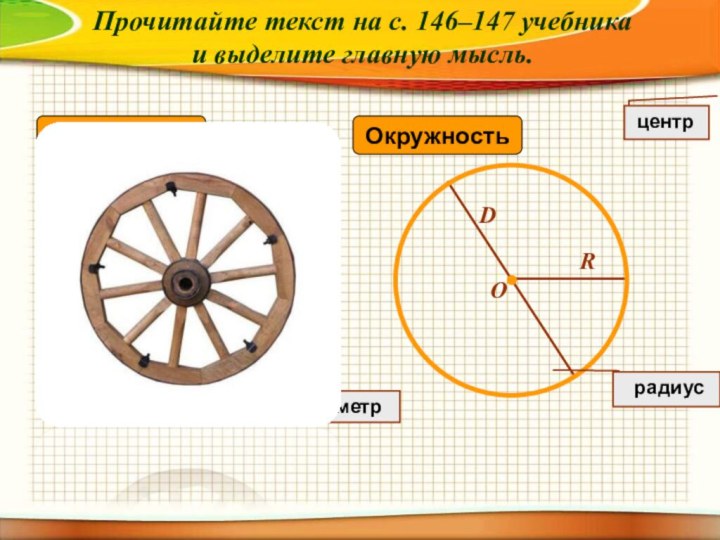
центр окружности.
3) Чем является отрезок АВ?
4) Есть ли на

чертеже еще диаметры?

A

чертеже еще радиусы?
7) Как называется отрезок DE?
8) Какой отрезок

называется хордой?

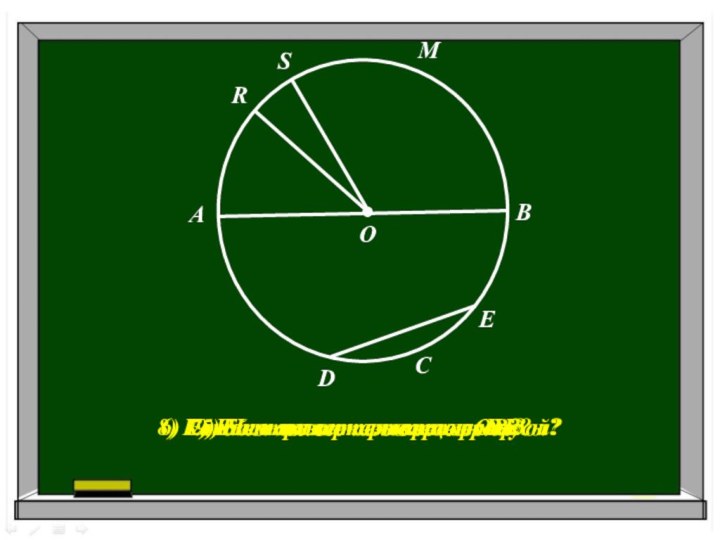
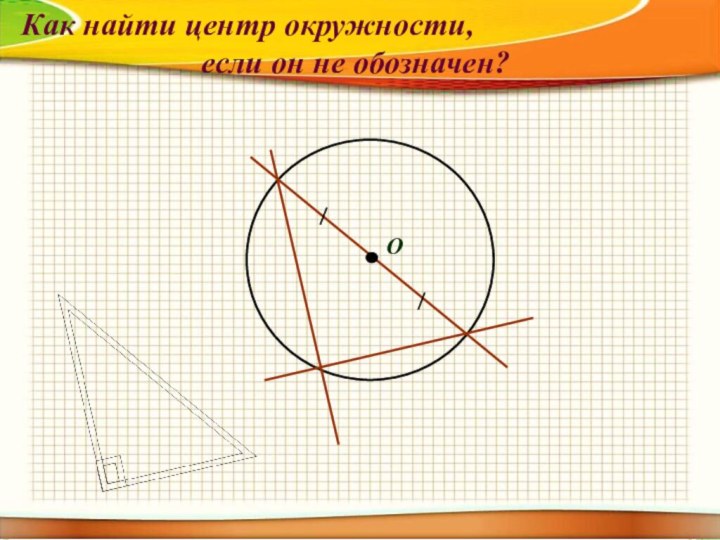
9) Есть ли на чертеже хорды?

длину радиуса?
12) С помощью какого измерительного прибора
это можно

сделать?

13) Какими единицами измерения будет
выражен результат?

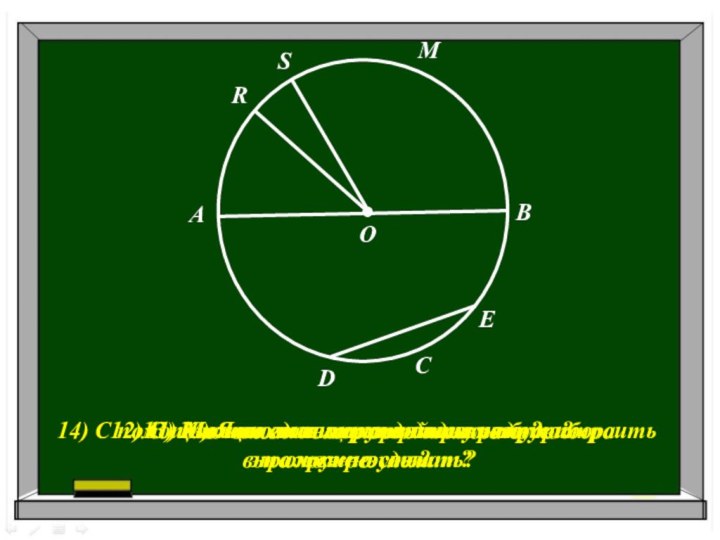
14) С помощью какого инструмента можно построить окружность?

главную мысль.
В известном романе английского писателя

- фантаста Герберта Уэллса рассказывается о вторжении на Землю марсиан. Сопротивление землян было подавлено марсианами без особого Труда, поскольку их оружие было намного эффективнее земного. К счастью, для землян всё закончилось благополучно - марсиане умерли от земного вируса, против которого у них не было иммунитета. При изучении оставшейся от марсиан техники выяснилось, что в ней отсутствуют колёса и вообще вращающиеся детали. Для нас это кажется невероятным - в наше время почти весь мир передвигается на колёсах. Но на самом деле далеко не всегда земная цивилизация была знакома с колесом. Так, например, американские индейцы и некоторые другие племена и народы Земли не знали колеса, пока туда не добралась европейская цивилизация. Однако, какому народу принадлежит первенство в изобретении колеса, доподлинно не известно.
Сравните рисунки 87, а и 87, б.

146–147 учебника
и выделите главную мысль.

изображено колесо, а на рисунке 87, б - его

математическая модель - окружность. У колеса, как и у окружности, есть радиус, диаметр и центр. Поскольку колесо ограничено двумя окружностями, внутренней и внешней, у него рассматривают два радиуса и два диаметра: для внутренней и для внешней окружностей. Измерить радиусы или диаметры внешней и внутренней окружностей колеса несложно. Но уже с древних времён перед людьми встала необходимость определять длину окружности колеса. Например, для того чтобы деревянное колесо дольше служило, его обивали металлическим ободом. Чтобы его изготовить, естественно, надо было знать длину этого обода, т. е. длину окружности колеса. Как же её определить?
Для внешней окружности это несложно: достаточно взять верёвку, обмотать ею колесо и измерить длину намотанной части верёвки. А как быть с внутренней окружностью? Можно, конечно, исхитриться и придумать какой-то способ, может быть, даже не один. Но ясно, что это гораздо сложнее, чем для внешней окружности.
Есть и другие примеры того, как сложно бывает измерить длину окружности. Но, как вы, наверное, уже убедились, математики ищут и зачастую находят простые способы решения разных проблем. Неизвестно, кому первому пришло в голову сравнить длину окружности с её диаметром, в частности узнать, во сколько раз длина окружности больше её диаметра. Ведь диаметр измерить значительно проще и, умножив длину диаметра на эту величину, можно было бы определить длину окружности

Прочитайте текст на с. 146–147 учебника
и выделите главную мысль.

стакана и запишите результаты измерений в таблицу
2. Положите

стакан на лист бумаги и обведите карандашом.
3. Измерьте с помощью линейки диаметр получившейся окружности и запишите результат измерения в таблицу.
4. Определите во сколько раз длина окружности больше ее диаметра, результат округлите до сотых и внесите в таблицу.

Лабораторная работа.

начальной буквы греческого слова περιφέρεια — окружность, периферия.
π=3,141592653589793238462643…

греческого слова περιφέρεια — окружность, периферия.
π=3,141592653589793238462643…
Архимед
≈3,142857142857143

греческого слова περιφέρεια — окружность, периферия.
π=3,141592653589793238462643…
Уильям Джонс
(1675 – 1749)
в

1706 году

начальной буквы греческого слова περιφέρεια — окружность, периферия.
π=3,141592653589793238462643…
Леонард Эйлер
(1707

– 1783)

начальной буквы греческого слова περιφέρεια — окружность, периферия.
π=3,141592653589793238462643…

в ласточек и облетим земной шар по экватору?
Давайте вычислим

длину экватора.

Задача:

Решение:

С ≈ 2 · 3,14 · 6370 ≈ 40003,6 м

С=2· π · r

Ответ: 40003,6 м.

1,5 см 

2. Найдите диаметр окружности, длина которой равна 7,85

м.

3. Найдите радиус окружности, длина которой 21,98 дм.

Применение понятия длина окружности в повседневной жизни.

3)Творческое задание: «Найти

интересные факты о числе π.

Домашнее задание:

запомнить цифры эти,
Нужно правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и

шесть.

π

π ≈ 3,1415926