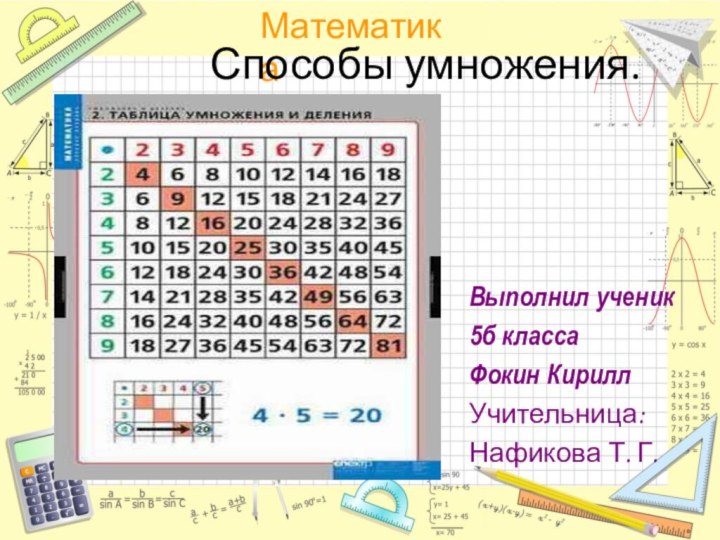
Слайд 2
Введение.
Во все времена математика была и остается

одним из основных предметов в школе, потому что математические
знания необходимы всем людям. Не каждый школьник, обучаясь в школе, знает, какую профессию он выберет в будущем, но каждый понимает, что математика необходима для решения многих жизненных задач: расчеты в магазине, оплата за коммунальные услуги, расчет семейного бюджета и т.д. Кроме того, всем школьникам необходимо сдавать экзамены в 9-м классе и в 11-м классе, а для этого, обучаясь с 1-го класса, необходимо качественно осваивать математику и прежде всего, нужно научиться считать.
Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Освоение вычислительных навыков развивает память и помогает усваивать предметы математического цикла. Существует много приемов упрощения арифметических действий.
Я хочу остановиться на способах умножения, для производства которых достаточно устного счета или применения карандаша, ручки и бумаги. Мотивацией для выбора темы послужило желание продолжения формирования вычислительных навыков, умения быстро и чётко находить результат математических действий. Правила и приёмы вычислений не зависят от того, выполняются они письменно или устно. Однако, владение навыками устных вычислений представляет большую ценность не потому, что в быту ими пользуются чаще, чем письменными выкладками. Это важно ещё и потому, что они ускоряют письменные вычисления, приобретают опыт рациональных вычислений, дают выигрыш в вычислительной работе. На уроках математики приходится, много делать устных вычислений и когда учитель показал нам приём быстрого умножения на числа 11 у меня возникла идея, а существуют ли ещё приёмы быстрого вычисления. Я поставил перед собой задачу, найти и опробовать другие приёмы быстрого вычисления.
Слайд 3
Цель исследования:
Изучить способы умножения, для производства которых достаточно устного
счета или применения карандаша и бумаги;
Помочь себе и товарищам
овладеть в совершенстве вычислительными навыками, и при этом, развивая память и внимание;
совершенствовать исследование и поисковые навыки учащихся.
В соответствии с поставленной целью были определены задачи:
1.Исследовать, применяют ли школьники приемы умножения.
2.Изучить старинные способы умножения, которые можно использовать, упрощая вычисления.
3.Составить памятку для учащихся 5-6 классов для применения приемов быстрого счета.
Слайд 4
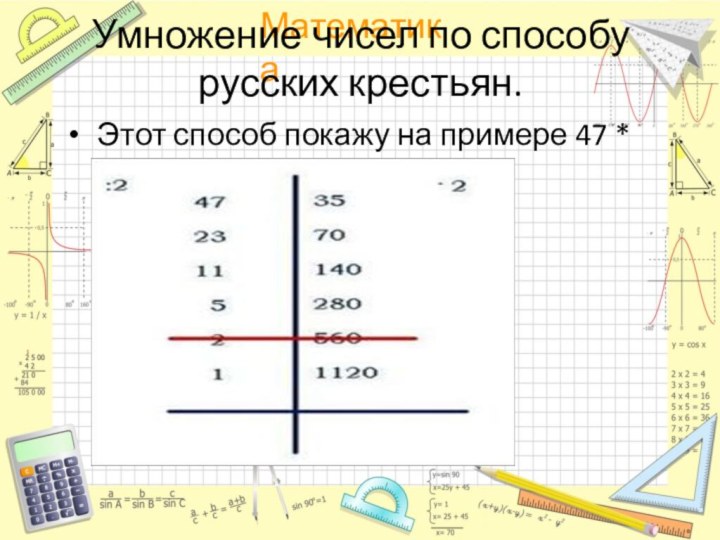
Этот способ покажу на примере 47 *
35:
Умножение чисел по способу русских крестьян.
188 + 3008 = 3196
Слайд 5
Индийский способ умножения
Американцам он настолько понравился, что они
его даже так и назвали «Американский способ». Однако им
пользовались жители Индии еще в VI в. н. э., и правильнее его назвать «индийским способом». Перемножить два каких - либо двузначных числа, скажем 23 на 12. Я сразу пишу, что получится.
х23
12
276
Вы видите: очень быстро получен ответ. Но как он получен?
Первый шаг: х23 говорю: «2 х 3 = 6»
12
…6
Второй шаг: х23 говорю: « 2 х 2 + 1 х 3 = 7»
12
.76
Третий шаг: х23 говорю: «1 х 2 = 2».
12 пишу 2 левее цифры 7
276 получаем 276.
Слайд 6
Египетский способ умножения
Обозначения чисел, которые использовались в древности,
были более или менее пригодны для записи результата счета.
А вот выполнять арифметические действия с их помощью было очень сложно, особенно это касалось действия умножения (попробуй, перемножь: ξφß*τδ). Выход из этой ситуации нашли египтяне, поэтому способ получил название египетского. Они заменили умножение на любое число - удвоением, то есть сложением числа с самим собой.
Пример: 34 ∙ 5=34∙ (1 + 4) = 34∙ (1 + 2 ∙ 2) = 34 ∙ 1+ 34 ∙ 4.
Т. к. 5 = 4 + 1, то для получения ответа оставалось сложить числа, стоящие в правом столбике против цифр 4 и 1 , т. е. 136 + 34 = 170.
Слайд 7
- запишем числа на одной строчке, проведём
между ними вертикальную черту;
- левое число будем делить на
2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);
- деление заканчивается, когда слева появится единица
- вычёркиваем те строчки, в которых стоят слева чётные числа;
- далее оставшиеся справа числа складываем – это результат; 35 + 70 + 140 + 280 + 1120 = =1645.
Слайд 8
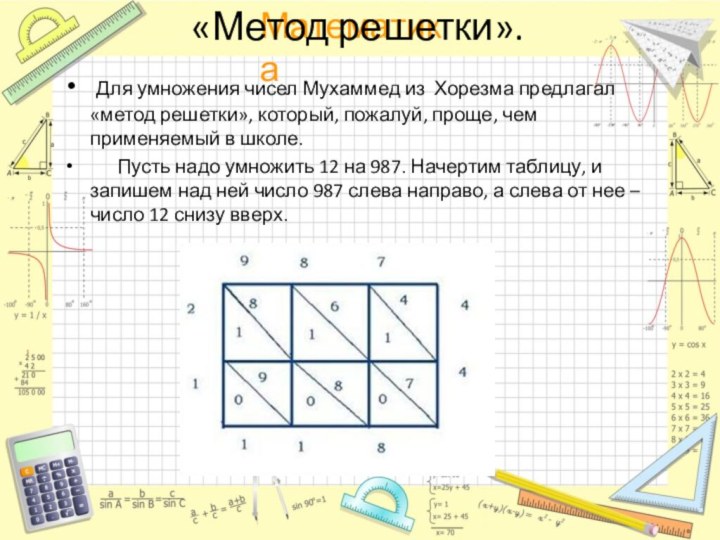
«Метод решетки».
Для умножения чисел Мухаммед из Хорезма
предлагал «метод решетки», который, пожалуй, проще, чем применяемый в
школе.
Пусть надо умножить 12 на 987. Начертим таблицу, и запишем над ней число 987 слева направо, а слева от нее – число 12 снизу вверх.
Слайд 9
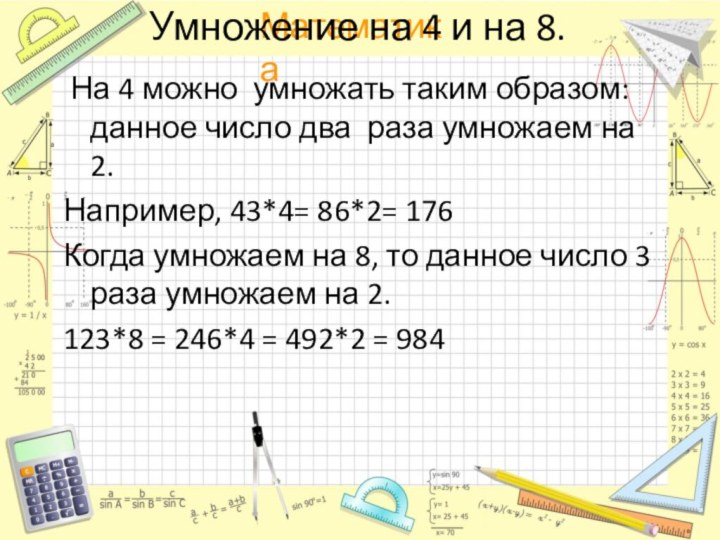
Умножение на 4 и на 8.
На 4
можно умножать таким образом: данное число два раза умножаем
на 2.
Например, 43*4= 86*2= 176
Когда умножаем на 8, то данное число 3 раза умножаем на 2.
123*8 = 246*4 = 492*2 = 984
Слайд 10
Умножение на 5.
Для того, чтобы умножать число на
5, надо это число разделить на 2 и полученному
результату приписать 0: 86 * 5 = 430
Если же число не делится на 2, то к неполному частному добавляем 5: 49*5 = 245
Слайд 11
Умножение на 9.
Чтобы умножать число на 9, его
надо сначала умножать на 10, потом из полученного числа
вычисть данное число. 345 * 9 = 3450 – 345= 3 105
Слайд 12
Умножение на 11.
А) Число умножать на 10
и прибавить это же число:
567 * 11
= 5670 + 567= 6237
Б) Если двузначное число умножаем на 11, то между цифрами этого числа вставить сумму цифр этого числа:
34 * 11= 3(3+4)4= 374
78 * 11 = 7 (3+8) 8 = 818
Слайд 13
Для умножения трёхзначных чисел на 11 так же

можно умножить трёхзначное или четырёхзначное число на 10 и
к произведению прибавить это же число, т.е. употребить первый из рассмотренных приёмов умножения на 11.
Познакомимся с приёмом умножения трёхзначного числа на 11 при помощи второго способа, он вытекает из письменного приёма умножения на 11.
758∙11=8338.
справа нужно записать число единиц множимого, т.е 8, затем к 8 прибавить следующее за ним слева число 5;
5 + 8 = 13; запишем 3, а 1 держим в уме.
далее 1 в уме прибавляем к 5 и складываем со следующим числом слева, с 7;
6 + 7 = 13, 3 пишем, а 1 добавим к 7, получим 8.
Можно этот приём применять и для четырёх- пятизначных чисел (и с большим числом знаков)
137542∙11=1512962
При известной сноровке такой приём умножения на 11 может быть полезен.
Умножения двузначного числа на 111 так же полезно запомнить
35∙111=3885 Мы видим, что по краям стоят числа 3 и 5 , а посредине повторяются дважды сумма цифр 3 и 5.
Также можно рассмотреть приём умножения двузначного числа на 1111:
52∙1111=57772
Умножения трёхзначных чисел на 11
Слайд 14
Умножения двузначного числа на 111
полезно запомнить
35∙111=3885
Мы
видим, что по краям стоят числа 3 и 5
, а посредине повторяются дважды сумма цифр 3 и 5.
Также можно рассмотреть приём умножения двузначного числа на 1111:
52∙1111=57
Слайд 15
Умножение на 25.
Для того, чтобы число умножать
на 25, данное число делим на 4 и умножаем
на 100.
44 * 25 = 1100
36 * 25 = 900
Если же число не делится нацело на 4, то поступаем таким образом: находим неполное частное и остаток от деления на 4, потом этот остаток умножаем на 25 и к неполному частному приписываем полученное произведение.
65 * 25 = 1625 (ост 1, 1*25= 25)
34*25 = 850 (ост 2, 2* 25=50)
67*25 = 1675 ( ост 3, 3*25 = 75)
Слайд 16
Умножение на 125.
Для того, чтобы число умножать
на 125, данное число делим на 8 и умножаем
на 1000.
328*125= 41000
256 * 125=32000
Слайд 17
Заключение.
Я знаю, что существуют много интересных способов вычислений.
И я соберу целою коллекцию таких примеров рационального вычисления.
Слайд 18
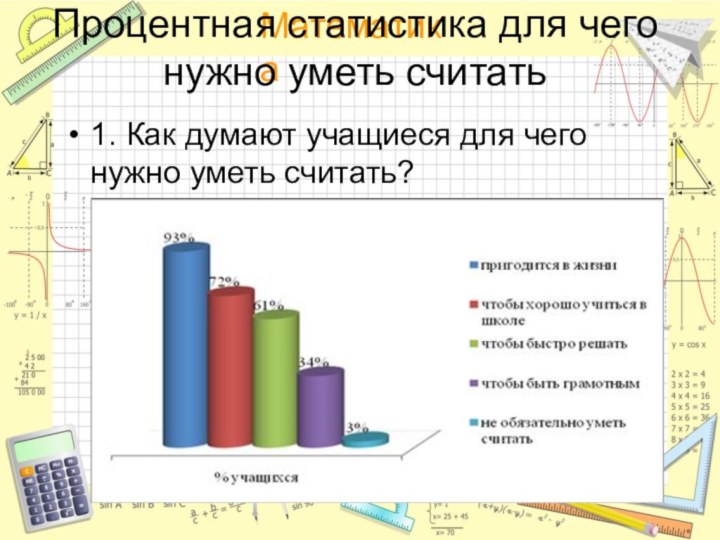
Процентная статистика для чего нужно уметь считать
1. Как
думают учащиеся для чего нужно уметь считать?
Слайд 19
При изучении каких школьных предметов тебе понадобится правильно
считать?
Слайд 20
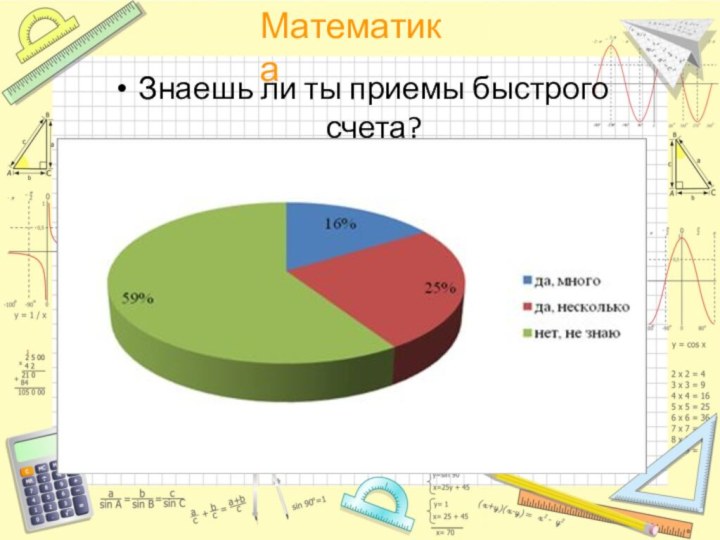
Знаешь ли ты приемы быстрого счета?
Слайд 21
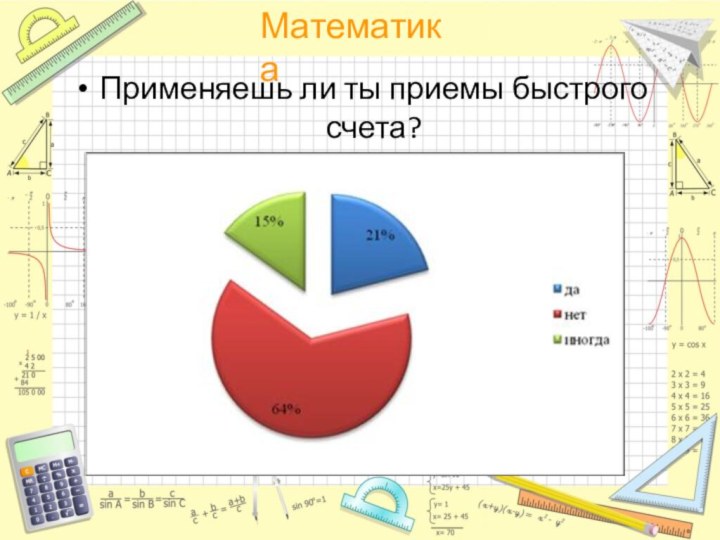
Применяешь ли ты приемы быстрого счета?
Слайд 22
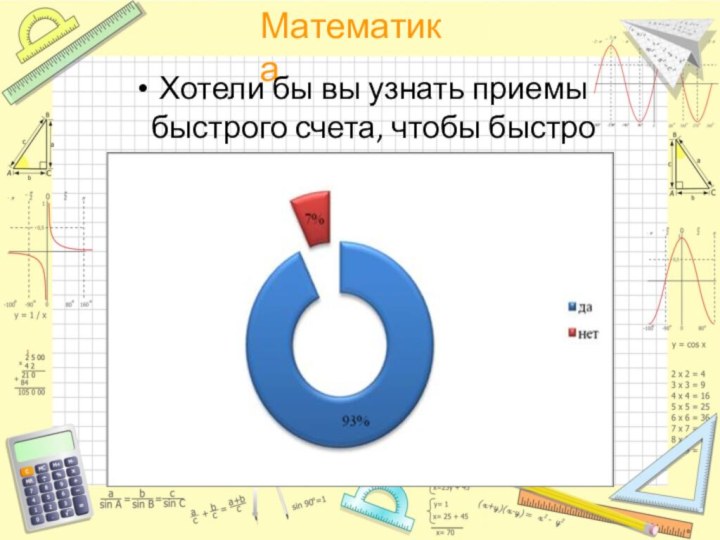
Хотели бы вы узнать приемы быстрого счета, чтобы
быстро решать?
Слайд 23
Литература.
Перельман.Я.И. Живая математика.-М.:Астрель:АСТ, 2005
Балаян.Э.Н.1001 олимпиадная и занимательная задачи
по математике. -3-е изд. – Ростов н/д:Феникс,2005
Чупиков П.В. Математика:
Школьные олимпиады: Методическое пособие.5-6 классы.- М.: ЭНАС,2004
Фарков А.В.Математика.Олимпиады в школе.5-11 класс. – 4-е изд. –М.:Айрис-пресс,2005.