Презентация на тему Презентація для студентів з математики Лінійна алгебра

у будівельній справі
Визначники. Властивості визначників
Правило трикутників
МінориМінори та алгебраїчні доповнення
Обернена

матриця
Системи лінійних рівнянь. Системи лінійних рівнянь. Метод Крамера

матриць у будівельній справі.
Визначники. Властивості визначників.
Правило трикутників.
Мінори та алгебраїчні

доповнення.
Обернена матриця.
8. Системи лінійних рівнянь. Метод Крамера.

– столбец
мінор - минор

де m – число рядків,

n - число стовпців
називається
матрицею.

*

і д п о в і д ь










Визначити

місце
елемента

А і В треба додати кожен елемент матриці А

з відповідним елементом матриці В







! можна додавати тільки матриці однакових розмірів

A+B=B+A

С+Д =








?

1

к = 3 ; кД =

К = -2; кД =

2

тільки тоді, коли кількість стовпчиків матриці А дорівнює кількості

рядків матриці В (матриці А і В називаються конформними) (4х3) ∙ (3х2) = (4х2) (3х2) ∙ (4х3) = ....

А (2х3)

В (4х2)

С (3х1)

D (4х5)
M (2х1)

AxC

BxA , BхM

Cx?

Dx?

Mx?

м а т р и ц ь

(2х2)∙(2х3)=(2х3)

3

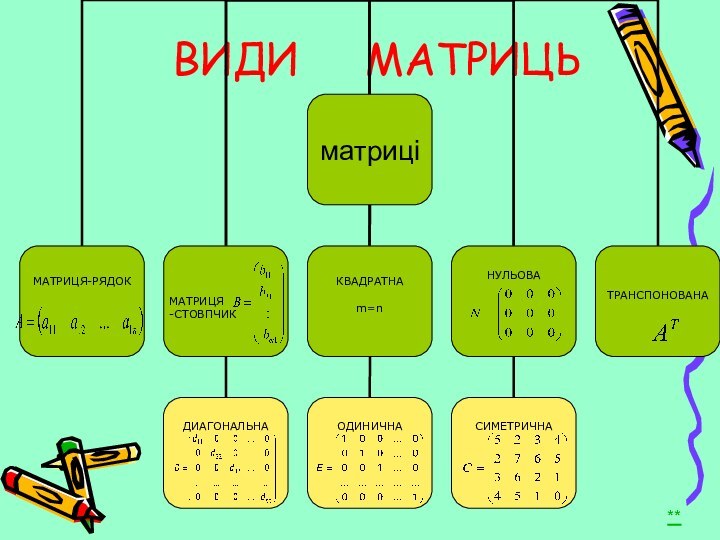
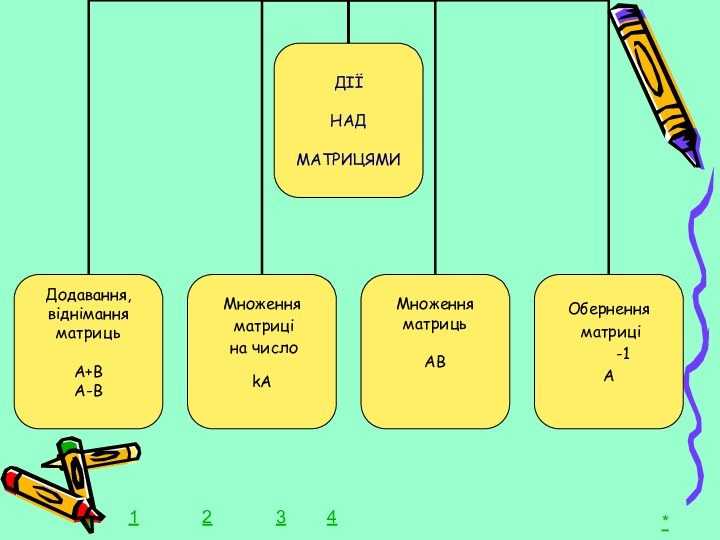
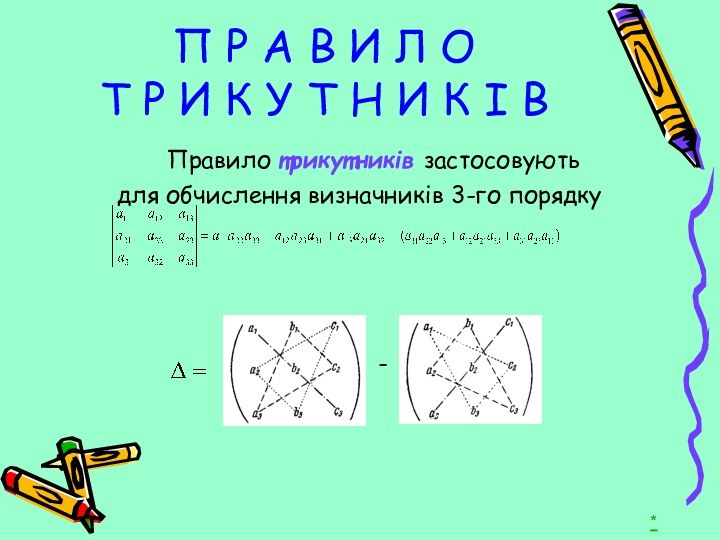
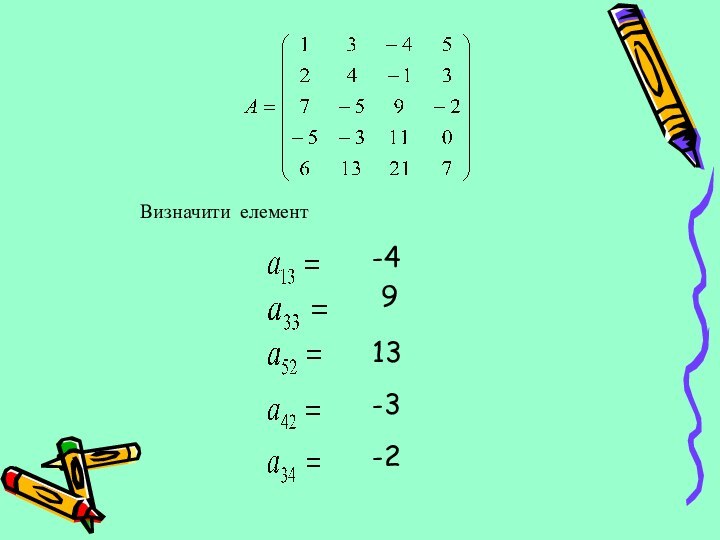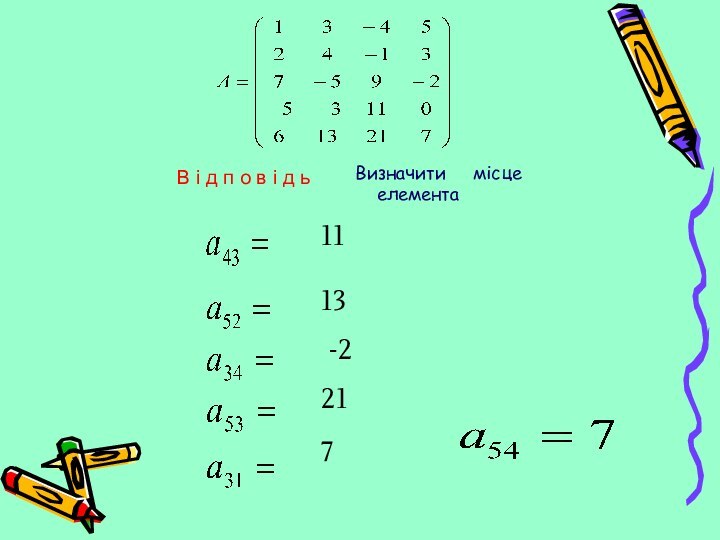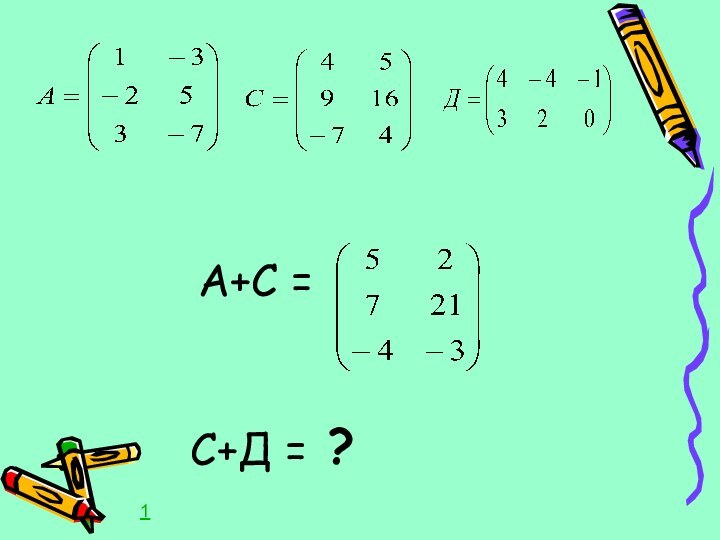множення матриць між собою звернемось до прикладу з виробництва.

ЗАДАЧА Комбінат ЖБК має три цехи в кожному з яких виготовляють різні види виробів.
Об’єм виробництва за квартал задається таблицею 1.
За цей час витрати на виробництво 1 тисячі штук виробів по сировині, електроенергії і води задаються таблицею 2
Знайти матрицю витрат на виробництво по цехах для сировини, електроенергії і води за І квартал











таблиця 1













таблиця 2

Перейдемо до матриць, позначивши
матрицю таблиці 1 через А,
таблиці 2 – через В

Очевидно, щоб визначити витрати І цеху на сировину ми повинні відповідно поелементно перший рядок матриці А помножити на перший стовпчик матриці В і знайти суму.
Далі перейдемо до ІІ цеху, візьмемо другий рядок матриці А і по черзі помножимо його на перший, другий і третій стовпчики матриці В. Аналогічно знайдемо витрати для ІІІ цеху

квадратною матрицею пов`язана певна числова

характеристика - визначник, який відповідає цій матриці.

Визначник квадратної матриці A позначається одним із символів:

det A, ∆, ∆(A),



Порядок визначника визначається за порядком квадратної матриці
для якої обчислюється визначник.
Визначником другого порядку, який відповідає матриці


називають число

В И З Н А Ч Н И К И

в л а с т и в о с

т і в и з н а ч н и к і в

Визначник транспонованої матриці дорівнює визначнику початкової матриці;
Якщо один з рядків (стовпчиків) складається тільки з нулів, то визначник дорівнює нулю;
При перестановці місцями двох рядків ( стовпчиків) визначника дістаємо визначник протилежного знаку;
Визначник. який має два однакові рядки (стовпчика), дорівнює нулю;
Якщо всі елементи деякого рядка(стовпчика) визначника помножити на число К, то сам визначник помножується на К;
Якщо один з рядків (стовпчиків) визначника пропорційний другому рядку, то визначник дорівнює нулю.
Визначник не змінюється, якщо до елементів одного з рядків (стовпчиків) додаються елементи другого рядка(стовпчика) помножені на одне й те саме число.

*

Т Р И К У Т Н И К

І В

Правило трикутників застосовують
для обчислення визначників 3-го порядку




-

*

називається визначник порядку(n-1), який одержується із матриці А

викреслюванням i-го рядка і j-го стовпчика.
Мінор позначається Мij

А=

М І Н О Р И

35

-29

10

-32

*

Ч Н І Д О П О В Н

Е Н Н Я

Алгебраїчним доповненням елемента матриці А на називається мінор цього елемента взятий зі знаком “ + “, якщо (i+j) - парне число або зі знаком “-”, якщо (i+j) - непарне
Алгебраїчне доповнення позначається

М21=51; М31=-39; М13=35;
А=
М23=10; М32=-29; М33=-32

А21=-51 ; А31=-39 ; А13=35

А23 = А33 =
А32 =

*

-10

29

-32

МАТРИЦЯ
Матриця А-1 називається оберненою до

матриці А, якщо АА-1=А-1А=Е.

де алгебраїчні доповнення
відповідних елементів матриці А.




А= ; det А=185

*

називають
системою лінійних
алгебраїчних рівнянь
загального виду

Якщо bi=0 лінійну систему називають однорідною

Існують системи з єдиним розв’язком , з кількома розв`язками,
і такі які не мають розв`язків.

*

СЛАР при m=n відмінний від нуля, то система рівнянь

має один єдиний розв`язок , який знаходиться за формулами,


; j = 1, 2,…, n.

Відповідь (1;0;-1)

*

т и с и с

т е м у

= - 31

= -31;

= 31;

= - 62;

*