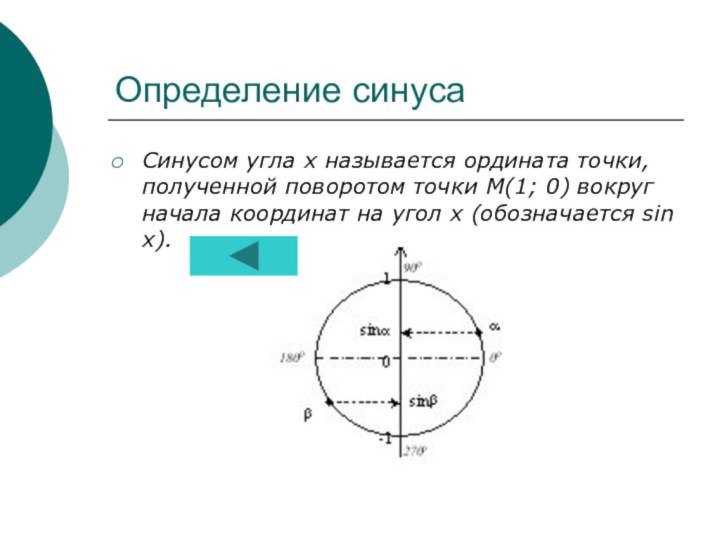
синуса...................................10
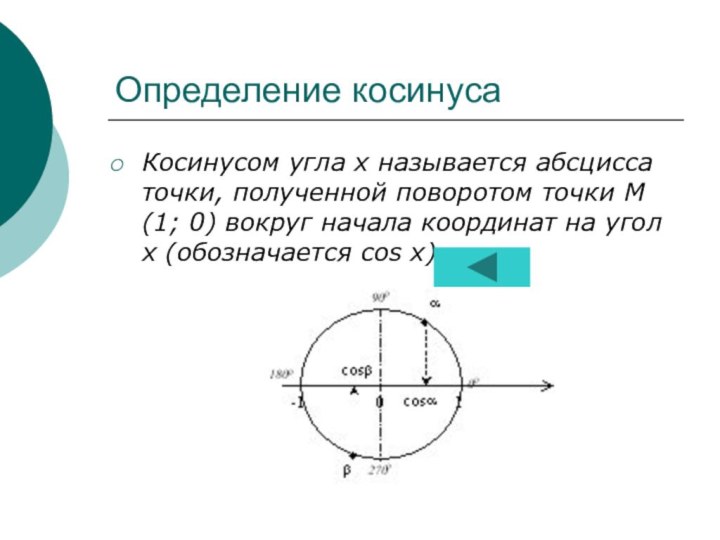
Определение и график косинуса...............................11
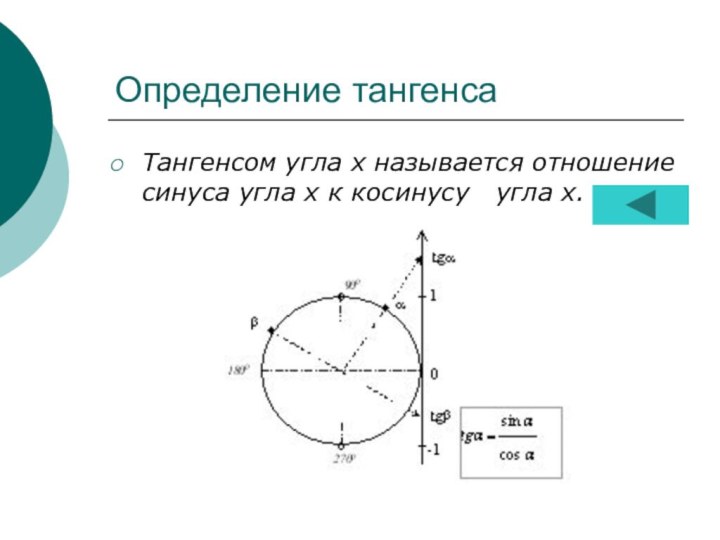
Определение и график тангенса...............................12
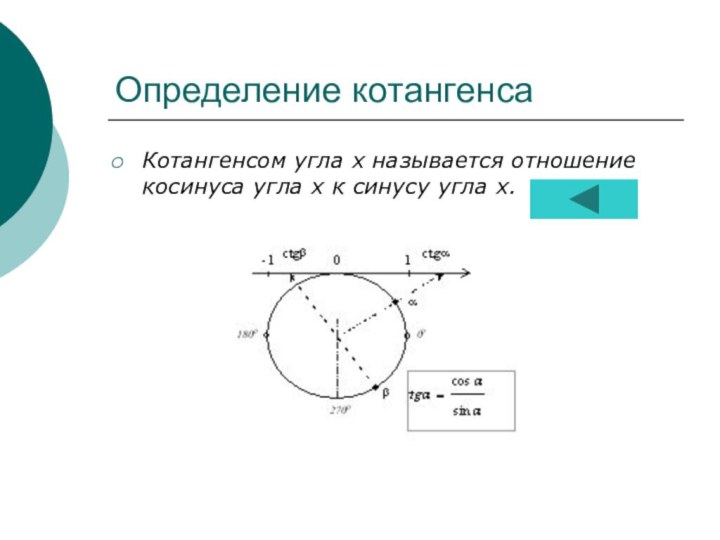
Определение и график
котангенса...........................13Обратные тригонометрические функции..................14
Основные формулы................................................15-16
Значение тригонометрии...........................................17
Используемая литература.........................................18