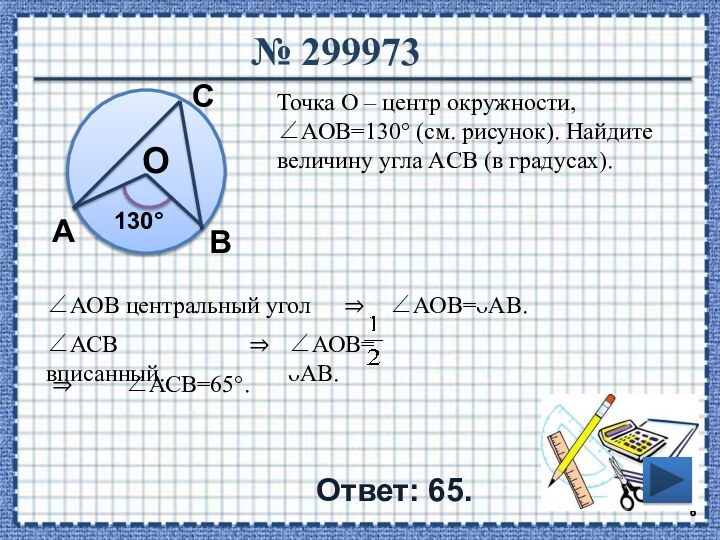
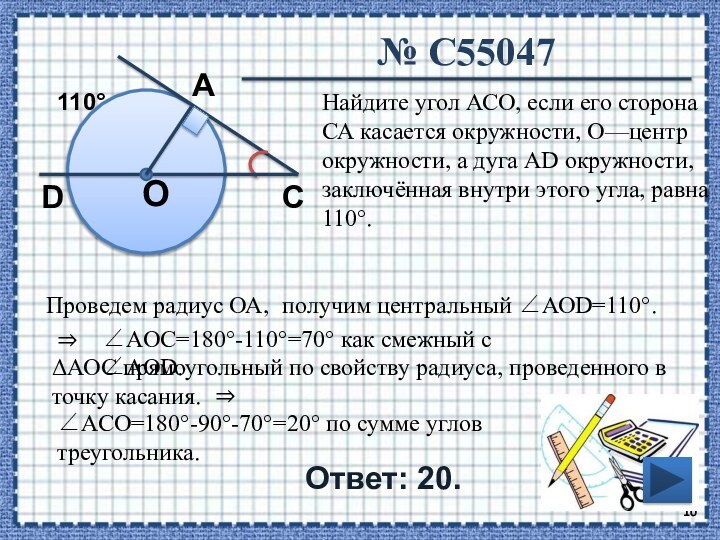
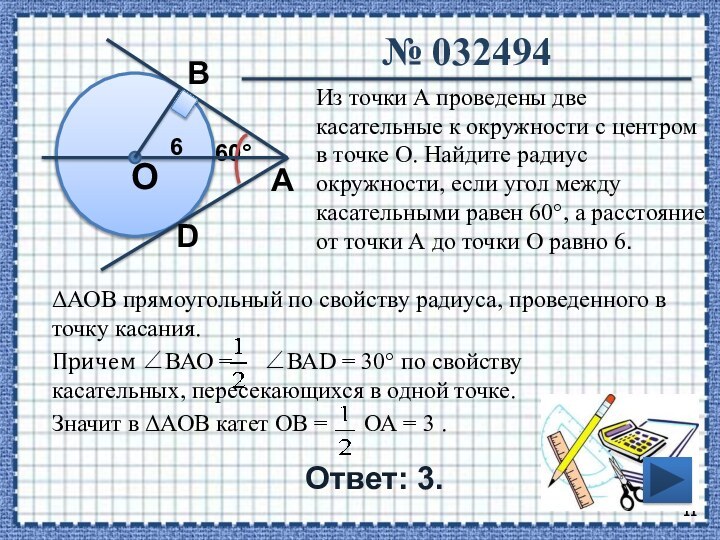
АВ так, что угол ОАВ равен 60°. Найдите длину
хорды АВ, если радиус окружности равен 8.В
А
ΔОАВ равнобедренный (ОА=ОВ=r), ⇒ ∠А=∠В.
О
60°
8
По сумме углов треугольника ∠О = 180°- (60°+ 60°) =60° .
В треугольнике против равных углов лежат равные стороны, ⇒
АВ=8.