х^2 – 3х + 4
у = 3 cosx
у = sin5x
у = tg(2 – 5х)
у = (х – 3)^2
у = (3 – 4х)^2
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



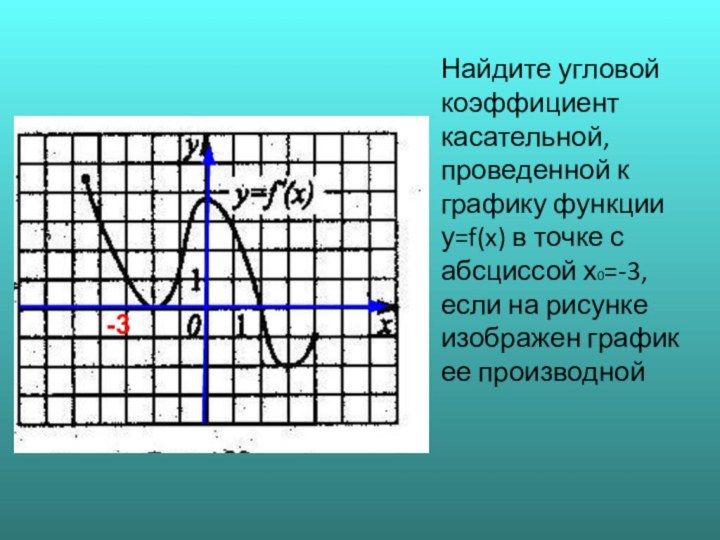
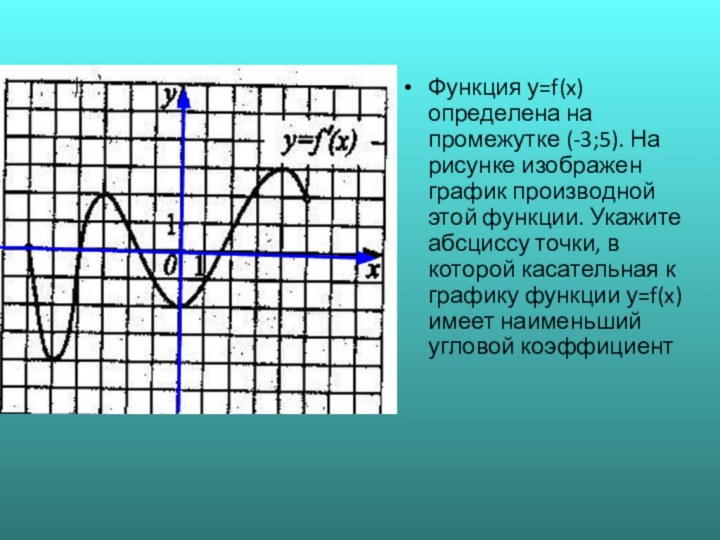




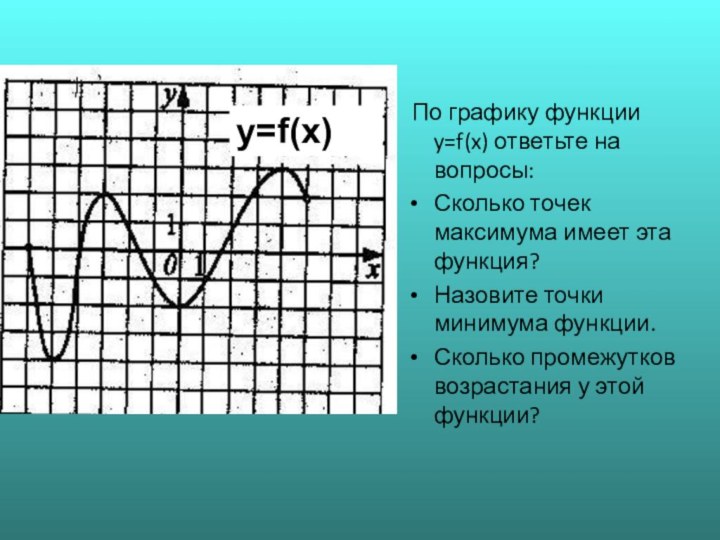




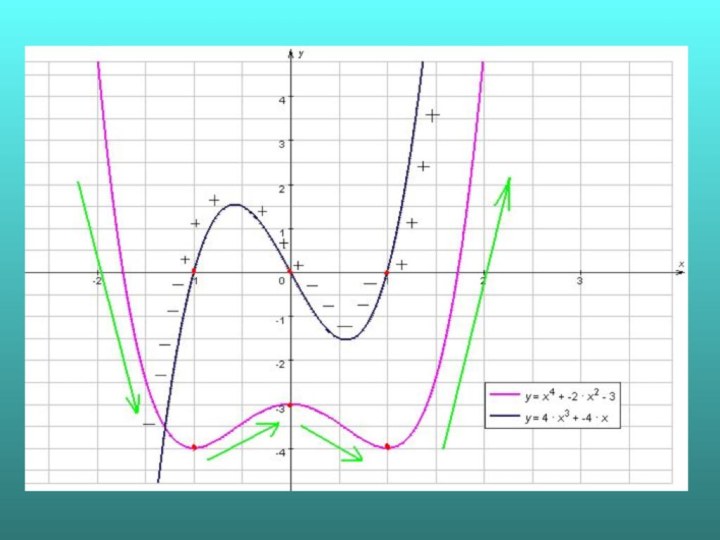
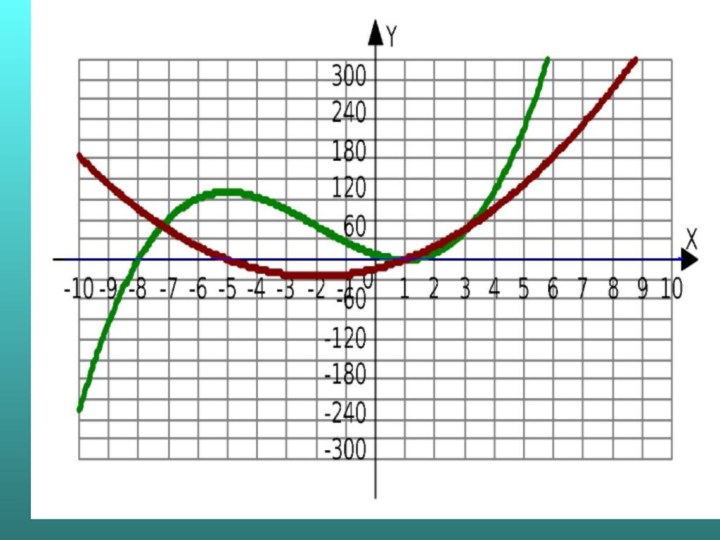


![Исследование функций на монотоноость №1. Непрерывная функция y=f(x) задана на [-6;5]. На рисунке изображён](/img/tmb/6/572969/b554b00ac4c779a6f06d51c488602fc8-720x.jpg)
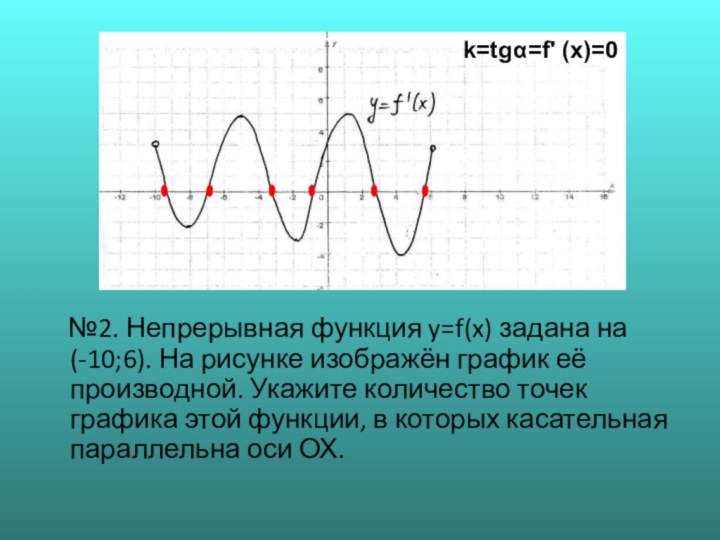




3
-3
1. Обозначить буквой a абсциссу точки касания.
2. Найти f(a).
3. Найти f '(x) и f '(a).
4. Подставить найденные числа a, f(a), f '(a) в общее уравнение касательной y = f(a) - f '(a)(x – a).
y=f(x)
k=tgα=f' (x)=0
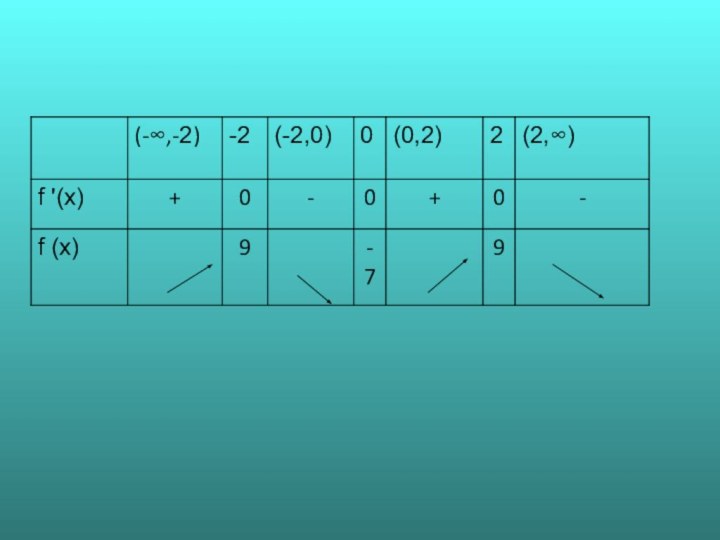
-2
0
2
+
-
+