Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Понятия математической статистики

Содержание

Случайные величиныСлучайной величиной Х (СВ) называется величина, которая в результате опыта может принять то или иное значение, причем заранее до опыта неизвестно, какое именно. Делятся на два типа: дискретные СВ (ДСВ) и непрерывные СВ (НСВ)
План занятия:Случайные величины Дискретная случайная величина (ДСВ)Закон распределения СВЧисловые характеристики ДСВТеоретические моменты Случайные величиныСлучайной величиной Х (СВ) называется величина, которая в результате опыта может Дискретная случайная величина (ДСВ)ДСВ – такая величина ,число возможных испытаний которой либо Законом распределения СВ называется соотношение, устанавливающее связь между возможным значением СВ и Закон распределения ДСВPiXix1x2x3x4p1p2p3p4Многоугольник распределенияСумма ординат многоугольника распределения, представляющая собой сумму вероятностей всех Повторение. Понятие вероятности. Вероятностью события А называется Р(А) =где п – множество Повторение. Теоремы о вероятностях. Теорема сложения вероятностей. Если события А и В Задача. Вероятности того, что студент сдаст экзамены в сессию по математике и Итак, закон распределения случайной величины Х задается таблицей:Контроль: 0,06+0,38+0,56=1.0,060,380,56 Числовые характеристики ДСВ1. Математическое ожидание М – сумма произведений значений СВ на Числовые характеристики ДСВСвойства математического ожидания: Числовые характеристики ДСВ2. Дисперсией ДСВХ называется математическое ожидание квадрата отклонения случайной величины План занятия:Случайные величины Дискретная случайная величина (ДСВ)Закон распределения СВЧисловые характеристики ДСВТеоретические моменты
Слайды презентации

Слайд 2 Случайные величины
Случайной величиной Х (СВ) называется величина, которая

Случайные величиныСлучайной величиной Х (СВ) называется величина, которая в результате опыта

в результате опыта может принять то или иное значение,

причем заранее до опыта неизвестно, какое именно.
Делятся на два типа: дискретные СВ (ДСВ) и непрерывные СВ (НСВ)

Слайд 3 Дискретная случайная величина (ДСВ)
ДСВ – такая величина ,число

Дискретная случайная величина (ДСВ)ДСВ – такая величина ,число возможных испытаний которой

возможных испытаний которой либо конечно, либо бесконечное множество, но

обязательно счетное.
Например, частота попаданий при 3 выстрелах – X
x1=0, x2=1, x3=2, x4=3
ДСВ будет полностью описана с вероятностной точки зрения, если будет указано, какую вероятность имеет каждое из событий.

Слайд 4 Законом распределения СВ называется соотношение, устанавливающее связь между

Законом распределения СВ называется соотношение, устанавливающее связь между возможным значением СВ

возможным значением СВ и соответствующими вероятностями.

Формы задания закона распределения:

1.

Таблица

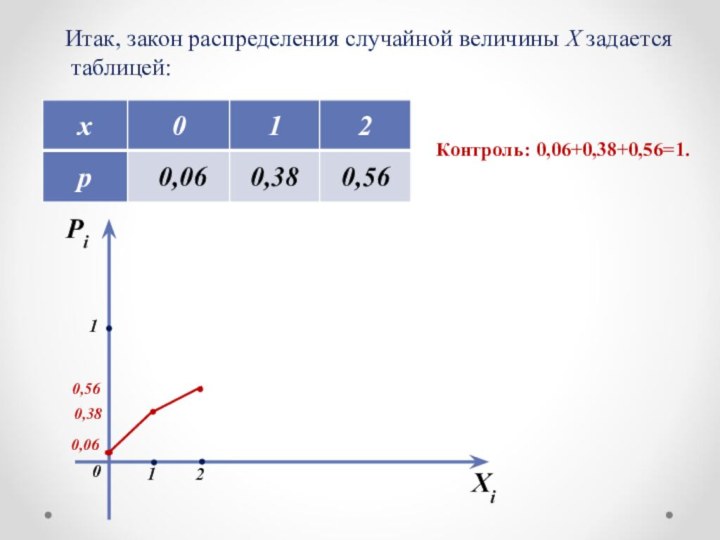
Закон распределения СВ

(Сумма всех вероятностей
равна 1)

Слайд 5
Закон распределения ДСВ
Pi
Xi
x1
x2
x3
x4
p1
p2
p3
p4
Многоугольник распределения
Сумма ординат многоугольника распределения, представляющая

Закон распределения ДСВPiXix1x2x3x4p1p2p3p4Многоугольник распределенияСумма ординат многоугольника распределения, представляющая собой сумму вероятностей

собой сумму вероятностей всех возможных значений СВ всегда равна

1.

Слайд 6 Повторение. Понятие вероятности. Вероятностью события А называется Р(А) =
где

Повторение. Понятие вероятности. Вероятностью события А называется Р(А) =где п –

п – множество всех исходов некоторого опыта;

т – множество положительных исходов некоторого опыта.

т
п


!Вероятность любого события не может быть больше 1 (или 100%)!

 

 

Слайд 7 Повторение. Теоремы о вероятностях.
Теорема сложения вероятностей. Если

Повторение. Теоремы о вероятностях. Теорема сложения вероятностей. Если события А и

события А и В несовместны, то вероятность их объединения

равна сумме их вероятностей.
Р(АUВ)= Р(А)+ Р(В).


Теорема умножения вероятностей. Если события А и В таковы, что они наступают одновременно, то вероятность совмещения событий равна произведению их вероятностей. Р(А∩В)=Р(А)∙Р(В).

Слайд 8 Задача. Вероятности того, что студент сдаст экзамены в

Задача. Вероятности того, что студент сдаст экзамены в сессию по математике

сессию по математике и органической химии соответственно равны 0,7

и 0,8.
Составить закон распределения случайной величины Х - числа экзаменов, которые сдаст студент.

Решение.
Рассматриваемая случайная величина X в результате экзамена может принять одно из следующих значений: x1=0, x2=1, х3=2.

 

 

 

 

Слайд 9 Итак, закон распределения случайной величины Х задается
таблицей:
Контроль:

Итак, закон распределения случайной величины Х задается таблицей:Контроль: 0,06+0,38+0,56=1.0,060,380,56

0,06+0,38+0,56=1.



0,06
0,38
0,56

Слайд 10 Числовые характеристики ДСВ
1. Математическое ожидание М – сумма

Числовые характеристики ДСВ1. Математическое ожидание М – сумма произведений значений СВ

произведений значений СВ на их вероятности.



Математическое ожидание является

характеристикой среднего значения случайной величины.

Слайд 11 Числовые характеристики ДСВ
Свойства математического ожидания:




Числовые характеристики ДСВСвойства математического ожидания:

Слайд 12 Числовые характеристики ДСВ
2. Дисперсией ДСВХ называется математическое ожидание

Числовые характеристики ДСВ2. Дисперсией ДСВХ называется математическое ожидание квадрата отклонения случайной

квадрата отклонения случайной величины от математического ожидания.


Дисперсия характеризует меру

рассеяния значений СВ от математического ожидания

(читать: дельта от икс)

При решении задач дисперсию удобно вычислять по формуле:



- Среднеквадратичное отклонение

  • Имя файла: ponyatiya-matematicheskoy-statistiki.pptx
  • Количество просмотров: 150
  • Количество скачиваний: 0
- Предыдущая Презентация к план-конспекту Роспись имбирного пряника по мокрой глазури.
Следующая - Презентация по ОБЖ на тему Повязки

Похожие презентации

Презентация по математике на тему Леонард Эйлер и его вклад в математическую науку. Презентация по математике на тему Леонард Эйлер и его вклад в математическую науку. 148
Часы. Секреты старого мастера. презентация к уроку по математике Часы. Секреты старого мастера. презентация к уроку по математике 61
Решение простейших геометрических задач (В4) Решение простейших геометрических задач (В4) 122
Вертикальные углы Вертикальные углы 193
Построение информационной модели метода изготовления изделия Построение информационной модели метода изготовления изделия 109
Таблица умножения и деления на 5. презентация к уроку по математике (2 класс) Таблица умножения и деления на 5. презентация к уроку по математике (2 класс) 210
Определение вероятности Определение вероятности 101
Графический диктант тренажёр по математике (2 класс) Графический диктант тренажёр по математике (2 класс) 63
Параллельные прямые в пространстве Параллельные прямые в пространстве 142
Экономический смысл производной Экономический смысл производной 140
Презентация урока математики по теме Коэффициент Презентация урока математики по теме Коэффициент 128
Презентация по математике на тему Сложение и вычитание десятичных дробей (5 класс) Презентация по математике на тему Сложение и вычитание десятичных дробей (5 класс) 111
Конспект мероприятия по познавательно-речевому развитию для детей старшего возраста Остров сокровищ презентация к занятию по математике (старшая группа) по теме Конспект мероприятия по познавательно-речевому развитию для детей старшего возраста Остров сокровищ презентация к занятию по математике (старшая группа) по теме 115
Геометрия в кристаллах Геометрия в кристаллах 169
Математическое лото Математическое лото 136
Найди фигуру презентация к уроку по математике (средняя группа) Найди фигуру презентация к уроку по математике (средняя группа) 141
Развёртки куба Развёртки куба 126
Решение неравенств с одной переменной и решение систем неравенств Решение неравенств с одной переменной и решение систем неравенств 100
Презентация Повторение пройденного вычисления вида +/-1,2,3. Решение тестовых задач. Презентация Повторение пройденного вычисления вида +/-1,2,3. Решение тестовых задач. 208
Презентация ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ Г.АЛАТЫРЬ Презентация ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ Г.АЛАТЫРЬ 147
Применение непрерывности Применение непрерывности 133
Доли.Урок математики в 3 классе презентация к уроку по математике (3 класс) Доли.Урок математики в 3 классе презентация к уроку по математике (3 класс) 128
Изучение таблицы деления Изучение таблицы деления 112
Презентация к фрагменту урока в 1 классе. Тема Числа и цифры 1 и 2 презентация к уроку по математике (1 класс) по теме Презентация к фрагменту урока в 1 классе. Тема Числа и цифры 1 и 2 презентация к уроку по математике (1 класс) по теме 116
Умножение рациональных чисел Умножение рациональных чисел 223
Математические тесты Математические тесты 124
Математический квест Путешествие в замке П для учащихся 6 классов Математический квест Путешествие в замке П для учащихся 6 классов 152
Презентация Математика и физика в хокее Презентация Математика и физика в хокее 153
Презентация к уроку математики Устный счет в 3 классе презентация к уроку по математике (3 класс) Презентация к уроку математики Устный счет в 3 классе презентация к уроку по математике (3 класс) 117
Звездный математический час Звездный математический час 111