красотой - красотой отточенной и строгой, возвышенно чистой и
стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».Бертран Рассел
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















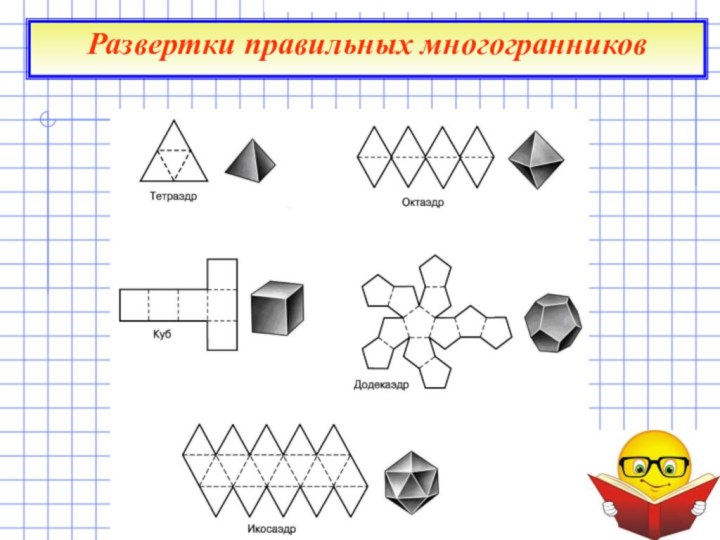

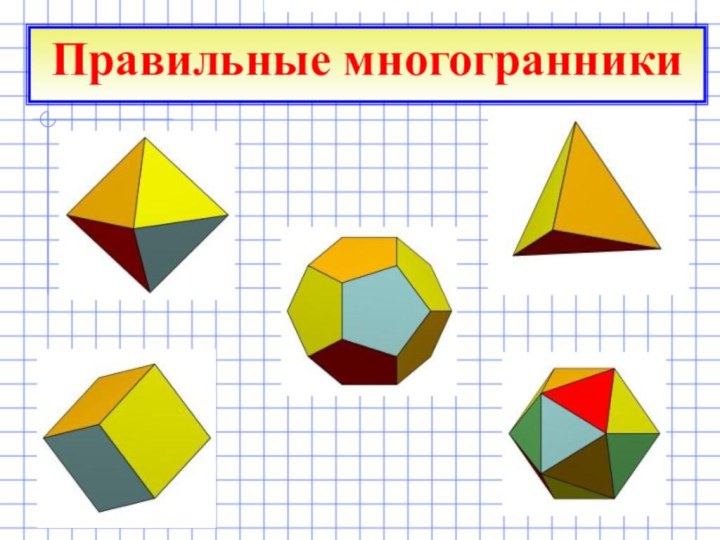

Задачи работы
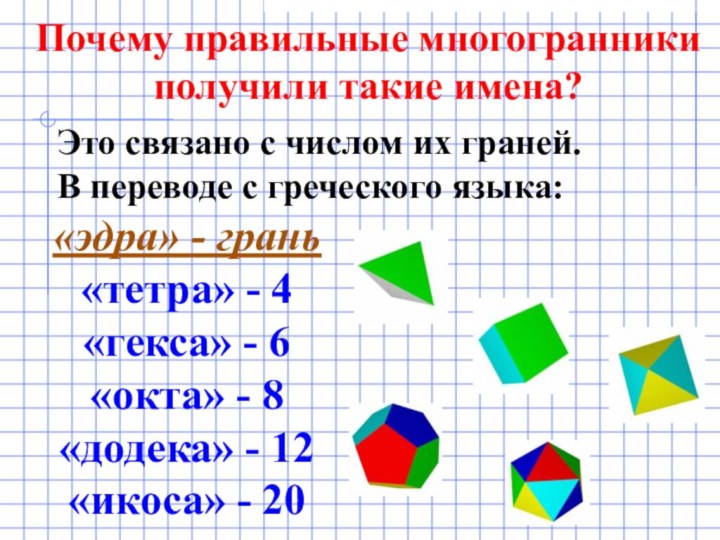
Это связано с числом их граней.
В переводе с греческого языка:
Г + В – Р = 2
Теорема Эйлера
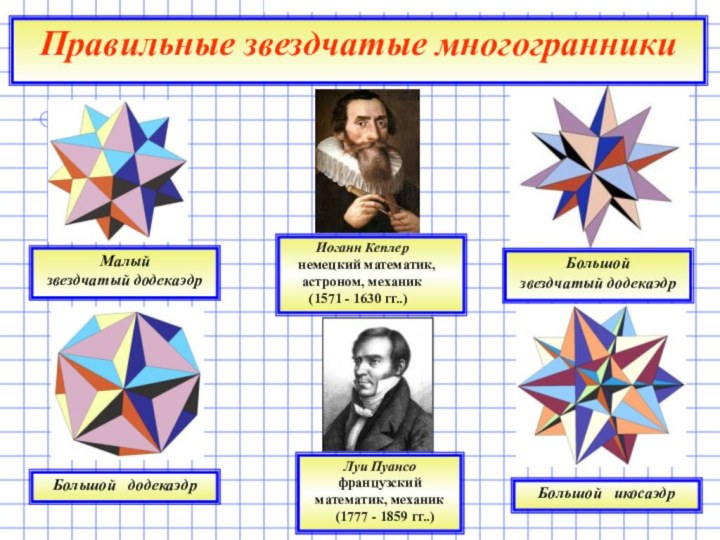
Луи Пуансо
французский
математик, механик
(1777 - 1859 гг..)