Презентация на тему по математике Проценты

двух чисел»,
переносить полученные знания, умения и навыки в

новую ситуацию,
выработать умения выполнять действия и преобразования, используя данные понятия.

Образовательная задача:

геометрическое моделирование;
положительная учебная мотивация;
разноуровневое обучение.

Краеугольные камни успешности в

изучении темы:

ему дробь:

фразу в правом

некоторой величины – это ее 50 %;

30 % величины

втрое больше, чем ее 10 %;

Эквиваленты

и 40 % пути на автобусе. Весь ли путь

они проехали?

Должны уметь отвечать на вопросы:

2. В классе 40 % девочек. Кого в классе больше – мальчиков или девочек?

3. Что больше:
а) 60 % всего класса или половина класса?

б) 10 % зарплаты или четверть зарплаты?

в) половина или 45 % всего населения страны?

была 100 руб., а стала 250 руб; б)

была 250 руб., а стала 100 руб.
2. Сколько было, если:
а) после увеличения на 30% стало 520 руб;
б) после уменьшения на 10% стало 450 руб.
3. В каком случае процентное отношение больше:
8 отличников из 40 учащихся или 9 отличников из 50 учащихся?
4. Сколько будет, если:
а) 150 руб. увеличить на 300%; б) 500 руб. уменьшить на 10%.
5. Сравни результаты:
150 руб. увеличили на 50% и 100 руб. увеличили на 100%.

Блиц-опрос

если известно несколько его процентов;
находить, сколько процентов одно

число составляет от другого.

Три вида задач на проценты

задач:

путем перевода числа процентов в дробь (десятичную или обыкновенную)

и далее умножения или деления на дробь,

использования пропорций.

Второй этап изучения – 6-й класс

процентов альбом дешевле книги?

Классические олимпиадные задачи

отрезком. Увеличим этот отрезок на 25 %, т.е. на

1/4 его часть; получим отрезок, соответствующий цене книги.
Теперь цена книги составляет 100%. Она изображена большим отрезком. Цена альбома меньше цены книги на 1/5 этого отрезка. Так как 1/5 составляет 20 %, то альбом дешевле книги на 20 %.









Ответ: на 20 %

Решение:

75%. Во сколько раз уменьшились цены?
(в 4 раза).

2)

На сколько процентов изменилась цена, если она была 100 руб., а стала 250 руб.?
(на 150% возросла)

Постройте графическую модель и решите следующие задачи:

автомобилей, в следующем месяце она увеличила выпуск игрушек на

200 %. Сколько игрушечных автомобилей стала выпускать фабрика? Во сколько раз увеличился выпуск игрушечных автомобилей? (480 игрушек; в 3 раза)

этого числа равны 90?

от числа 120?

х = 30.
Ответ: 30 г

Сколько граммов воды надо добавить к 50 г раствора, содержащего 8% соли, чтобы получить 5%-й раствор?

90% воды,
а сушеный 15%.
Сколько получится сушеных

грибов из 17 кг свежих?
Сколько надо взять свежих грибов, чтобы получить 3,54 кг сушеных?

Сколько получится сушеных грибов из 17 кг свежих?


100 –

90 = 10 (%) - приходится на сухое вещество в свежих грибах.
17 : 10 =1,7(кг) - масса сухого вещества в 17 кг свежих грибов и в сушёных грибах.
100 – 15 = 85(%) - приходится на сухое вещество в сушёных грибах.
1,7 : 85 = 0,02 (кг) - приходится на 1% массы сушёных грибов.
0,02 · 100 = 2 (кг) - масса сушёных грибов.

Ответ: 2 кг сушёных грибов получится из

17 кг свежих грибов.

и ширину увеличить на 10%? (увеличится на 21%)
2. Как

изменится площадь прямоугольника, если его длину и ширину уменьшить на 10%? (уменьшится на 19%)
3. Как изменится площадь прямоугольника, если его длину увеличить на 30%, а ширину уменьшить на 30%? (уменьшится на 9%)
4. Как изменится объем куба, если длину его ребра увеличить на 20? (увеличится на 72,8%)

Классические задачи на проценты для 7-9 классов

а затем снизили на 15%. Сравните окончательную и первоначальную

цену товара
(уменьшилась на 2,25%)
6. На распродаже цену на костюм снизили на 20%.
На сколько процентов надо повысить новую цену, чтобы вернуться к первоначальной?
(на 25%)

задачи на проценты»

это 0,01 или 1/100
Полезно также запомнить: при решении задач

на проценты число,
с которым сравнивают другое число, принимают за 100%.

Напомним основные соотношения и выражения, встречающиеся при решении задач на проценты.
Предложение «Число a составляет р% от числа b» выражается равенством а= b/100*р
Предложение «Число а увеличили на р%» представляется выражением а(1+0,01р).
Предложение «Число а увеличили сначала на р%, а потом еще на q % » представляется выражением
а(1+0,01р)(1+0,01q).
Предложение «Число а уменьшили на р%» представляется выражением
а(1-0,01р).
Предложение «Число а увеличили на р%, а потом уменьшили на q%» представляется выражением
а(1+0,01р)(1-0,01q).
При ответе на вопрос «На сколько процентов число а больше числа b?» требуется найти значение выражения (а- b)/ b *100%

Учимся решать задачи на проценты

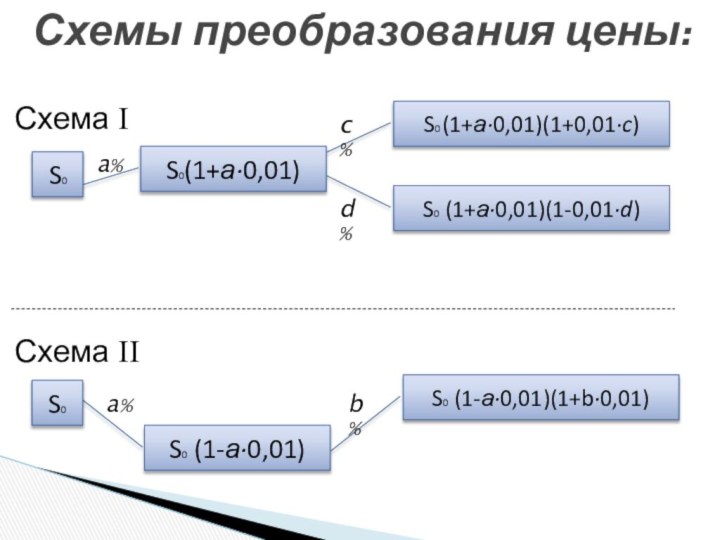
S – новая (окончательная)

цена.
Решение подавляющего большинства задач этого вида опирается на применение следующих формул: 
1. После повышения цены товара на а% ее новое значение
S= S0(1+а·0,01),
а после понижения цены на а%
S= S0 (1-а·0,01).
2. В результате повышения цены товара на а% и последующего понижения на b% ее новое значение
S = S0 (1+а·0,01)(1-b·0,01).
Аналогично, если цена сначала понизилась на а %, а потом повысилась на b%, то
S = S0(1-а·0,01)(1+b·0,01).
3. Если цена товара повышалась n раз на a%, то ее окончательное значение S = S 0(1+а·0,01)n
а если цена понижалась n раз на b%, то
S= S 0(1-b·0,01)n

Задачи, связанные с изменением цены

цены:

= S0 (1- 25 ·0,0001)=
=S0(1- 0,25·0,01).

Ответ: цена понизилась

на 0,25%.

Решение. Составим схему преобразований исходной цены

Задача 1. Цена товара сначала понизилась на 5%, а затем повысилась на 5%.
Изменилась ли (повысилась или понизилась) первоначальная цена товара, и если «да», то на сколько процентов.

·0,01)(1+ 30·0,01) = 1,25(1+ 30 ·0,01),

S 0 = 1.

Ответ: 1 тыс.руб.

Преобразования цены на первый товар

Преобразования цены на второй товар

Задача 2. Цена на некоторый товар сначала поднялась на 25%, а потом еще на 30%. Другой товар поднялся в цене на 30%, и его новая цена стала равна новой цене первого товара. Какова исходная цена первого товара, если второй до повышения цены стоил 1,25 тыс. руб.?

х = 160 или х = 20.
При х=20 получим, что товар стоил после первого понижения 2520 руб.

Задача 3. Некоторый товар стоил 3150 руб. После двух последовательных понижений цены он стал стоить 1512 руб. Сколько стоил товар после первого понижения, если второе понижение было на 20% больше, чем первое?

Решение. Пусть x – процент первого понижения, тогда (х+20) - процент второго понижения.

Схема преобразований цены товара:

Уравнение ¾ S0(1+ х·0,01)(1+2х·0,01)= 2,64 S0
x²+150x-12600=0 x = 60, x = -210.
Новый процент по вкладу составил 120%.
Ответ: 120%.

Решение. Пусть S0 - положенная в банк сумма,
x% - первоначальный процент годовых.

Задача 1. Клиент положил деньги в банк под определенный процент годовых и через год снял ¼ часть получившейся суммы. На следующий год банк увеличил процент годовых в два раза. К концу второго года сумма вклада превысила первоначальную сумму на 164%. Чему равен новый процент годовых, установленный банком?

S0 - сумма выданного кредита.
Уравнение: 0,25S0 (1+x·0,01)²=1,21S0

x=120, x= -300
Ответ: 120%.

Задача 2. Фермер взял в банке кредит под некоторый процент годовых. Через год в счет погашения кредита он вернул банку ¾ всей суммы, которую был должен к этому времени, а еще через год в счет полного погашения кредита внес сумму, на 21% превышающую величину полученного кредита. Чему равен процент годовых по выданному кредиту?

а затем новая цена понижена на 10%. Найти процентное

отношение последней цены к первоначальной.