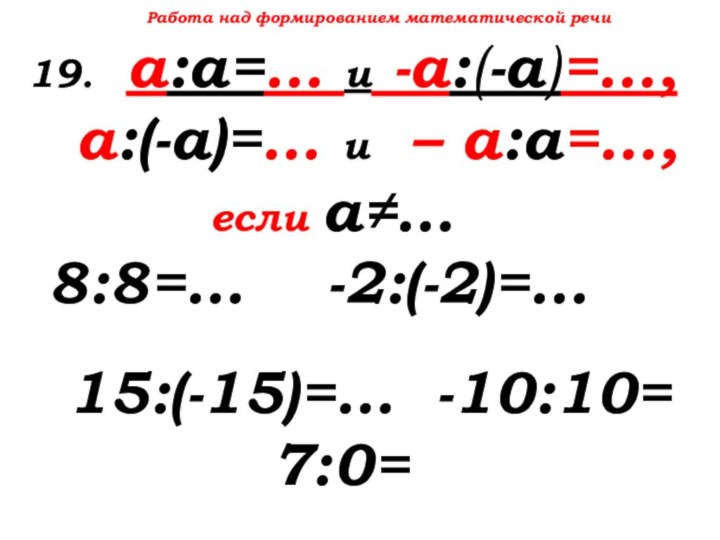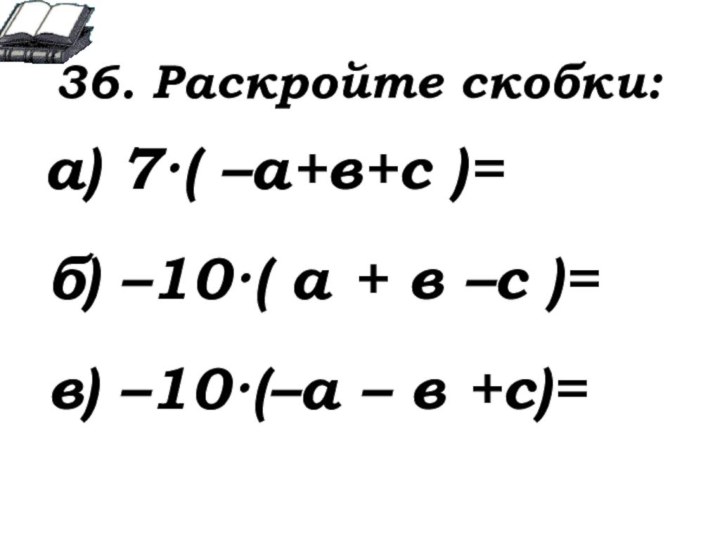Успешного
усвоения нового материала
Решение трудной математической проблемы можно сравнить с взятием крепости.
Наум Яковлевич Виленкин
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок №154 Подобные слагаемые, 6 класс
Содержание
- 2. Девиз урока
- 3. Блиц-опрос
- 4. Работа над формированием математической речи1. Сумма 0
- 5. Работа над формированием математической речи3. Сумма противоположных
- 6. Работа над формированием математической речи5. Произведение 0
- 7. Работа над формированием математической речи7. Числа при
- 8. Работа над формированием математической речиа·(-1) = …
- 9. Работа над формированием математической речи11. Произведение взаимно
- 10. Работа над формированием математической речи13. Частное 0
- 11. Работа над формированием математической речи16. Частное любого
- 12. Работа над формированием математической речи17. Частное любого
- 13. Работа над формированием математической речи19. а:а=… и
- 14. Работа над формированием математической речи20. При возведении
- 15. Работа над формированием математической речи22. Чтобы сложить
- 16. Работа над формированием математической речи23. Чтобы сложить
- 17. Работа над формированием математической речи24. Чтобы перемножить
- 18. Работа над формированием математической речи25. Чтобы разделить
- 19. Работа над формированием математической речи27. При делении
- 20. 29. При возведении в куб: - положительного
- 21. 31. Если ху= 0,то имеем 3 случая:1)
- 22. 33. Если перед скобками стоит знак+ ,
- 23. 34.Если перед скобками стоит знак – ,
- 24. 35. Коэффициентами в
- 25. 36. Раскройте скобки:
- 26. Проверка Д.Р № 127 на 05.04.18
- 27. Стр. 224, №1280Д.Р № 127, на
- 28. Стр. 227, № 1295Д.Р № 127, на 05.04.18
- 29. Стр. 227, № 1295Д.Р № 127, на 05.04.18
- 30. Стр. 227, № 1295Д.Р № 127, на 05.04.18
- 31. Стр. 228, № 1304 (а,б,в)Д.Р №
- 32. Оцените
- 33. Подобные слагаемые п.4105.04.2018К.Р.
- 34. Цели урока:Ввести понятие «подобные слагаемые».Учиться складывать подобные слагаемые. Развивать письменную и устную математическую речь.
- 35. Стр. 225, №1281(в,г,д)Письменно в тетради c пояснением
- 36. Стр.
- 37. Стр.
- 38. Стр.
- 39. Стр.
- 40. Стр.
- 41. Стр. 225, №1281(в,г,д)Письменно в тетради г) –а·(6b –3c +4)=…–…+…
- 42. Стр.
- 43. Стр.
- 44. Стр.
- 45. Стр.
- 46. Стр.
- 47. Стр.
- 48. Стр.
- 49. Стр.
- 50. Стр.
- 51. Стр.
- 52. Стр.
- 53. Стр.
- 54. Стр.
- 55. Стр.
- 56. Стр.
- 57. Стр.
- 58. Стр. 225, №1282(а,б,в,г)С пояснением Вынесение общего
- 59. Стр.
- 60. Изучение нового материала
- 61. Изучение нового материала
- 62. Изучение нового материала
- 63. Изучение нового материала
- 64. Изучение нового материала
- 65. Стр. 225, №1283(а,г,ж)Письменно в тетради c пояснением
- 66. Стр.225,
- 67. Стр.225,
- 68. Стр.225,
- 69. Стр.225,
- 70. Стр.225,
- 71. Стр.225, №1283(а,г,ж)Письменно в тетради c пояснением г) –3,8k–k+3,8k+k==(–3,8–1+3,8+1)·k=
- 72. Стр.225, №1283(а,г,ж)Письменно в тетради c пояснением г) –3,8k–k+3,8k+k==(–3,8–1+3,8+1)·k=
- 73. Стр.225, №1283(а,г,ж)Письменно в тетради c пояснением г) –3,8k–k+3,8k+k==(–3,8–1+3,8+1)·k=
- 74. Стр.225, №1283(а,г,ж)Письменно в тетради c пояснением г) –3,8k–k+3,8k+k==(–3,8–1+3,8+1)·k= 00
- 75. Стр.225,
- 76. Стр.225,
- 77. Стр.225,
- 78. Стр.225, №1283(а,г,ж)Письменно в тетради c пояснением
- 79. Стр.225, №1283(а,г,ж)Письменно в тетради c пояснением
- 80. Стр.225, №1283(а,г,ж)Письменно в тетради c пояснением
- 81. Устная работа. Итоги урока 1. Вычислите: а) 7·14+7·6=б) 7·16 – 7·6=
- 82. Итоги урока 2.
- 83. Итоги урока 3.
- 84. Итоги урока Оцените свое настроение по итогам урока: Все понятно Остались некоторые вопросы Требуетсяпомощь
- 85. Скачать презентацию
- 86. Похожие презентации
Девиз урока Успешного усвоения нового материала Решение трудной математической проблемы можно сравнить с взятием крепости. Наум Яковлевич Виленкин
Слайд 2
Девиз урока
Слайд 4
Работа над формированием математической речи
1. Сумма 0 и
любого числа равна этому же …
0+ (-а ) =…
а + 0 =…0+ (-3)=… 5+ 0 =…
2. Если произведение двух чисел ху<0,
то х и у имеют …знаки
Слайд 5
Работа над формированием математической речи
3. Сумма противоположных чисел
равна …
а+(-а )= … -
а+ а=…6+(-6)=… - 7+ 7=…
4.Если произведение двух чисел ху>0,
то х и у имеют … знаки
Слайд 6
Работа над формированием математической речи
5. Произведение 0 и
любого числа равно …
0 · а= … 0·(-
а)= …0 · 8= … 0·(- 9)= …
6. Числа при вычитании называются …,…,… .
а – в = с
Слайд 7
Работа над формированием математической речи
7. Числа при сложении
называются …,…,… .
а + в = с
8. Произведение числа
и 1 равно … … . а·1= … 1·(- а)= …
9·1= … 1·(- 7)= …
Слайд 8
Работа над формированием математической речи
а·(-1) = … -
а·(-1)= …
5·(-1) = … - 7·(-1)= …
10. Числа при
делении называются …,…,… . а : в = с
9. Произведение числа и -1 равно … … .
Слайд 9
Работа над формированием математической речи
11. Произведение взаимно обратных
чисел равно …
12. Числа при умножении называются …,…,…
.а · в = с
Слайд 10
Работа над формированием математической речи
13. Частное 0 и
любого числа,
отличного от 0, равно…
0:а=…и 0:(-а)=…,если а≠…
0 : 5=… ; 0:(-2)=…
14. Если х:у= 0, то:
х…0, а у…0.
0:3=… 0:(-5)=…
Слайд 11
Работа над формированием математической речи
16. Частное любого числа
и 1 равно… … а:1=…;–а:1=…
2:1=…
-3:1 15. Чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, … вычитаемому.
а – в= а + (– …)
3 – 4=… –9 – 6=…
Слайд 12
Работа над формированием математической речи
17. Частное любого числа
и -1 равно … …а:(-1)=…; –а:(-1)=…
7 :(-1)=…и
-6:(-1) =… Чтобы перемножить два отрицательных числа, надо перемножить их … .
– 7·(– 9)=
Слайд 13
Работа над формированием математической речи
19. а:а=… и -а:(-а)=…,
а:(-а)=… и – а:а=…,
если а≠… 8:8=… -2:(-2)=…
15:(-15)=… -10:10=
7:0=
Слайд 14
Работа над формированием математической речи
20. При возведении в
квадрат любого числа получается
либо положительное число, либо…
3²=…
(-3)²=… 0²=… 21.Раскройте скобки:
а + ( –т+с –к)= …
-а – ( в –п – с)= …
Слайд 15
Работа над формированием математической речи
22. Чтобы сложить два
отрицательных числа, надо:
1) сложить их …
2) поставить перед полученным
числом знак …–5+(–7)=… (–6) + (–4)=…
–5 – 7=… –6 – 4 =…
Слайд 16
Работа над формированием математической речи
23. Чтобы сложить два
числа с разными знаками, надо:
найти … каждого слагаемого;
из… модуля
вычесть … ;поставить перед полученным числом знак …, модуль которого…
–5+8=… –10+8=…
–5+2=… –10+18=…
Слайд 17
Работа над формированием математической речи
24. Чтобы перемножить два
числа с разными знаками, надо перемножить их … и
поставить перед полученным произведением знак …– 7·2=…
9·(– 3)=…
– 0,7·10=…
5·(–1,1)=…
0·(–3,1)=…
Слайд 18
Работа над формированием математической речи
25. Чтобы разделить отрицательное
число на отрицательное, надо разделить модуль … на …
делителя.– 8:(–2)=…
26.Раскройте скобки:
-а + (- в – с –р)= …
а – ( в – с+т)= …
Слайд 19
Работа над формированием математической речи
27. При делении чисел
с разными знаками, надо:
разделить …делимого на модуль … ;
поставить
перед полученным числом знак … .–8:2=…
9:(–3)=…
2:(–3)=…
28. Раскройте скобки:
а + ( т+с –к)= …
-а – ( в –п – с)= …
Слайд 20
29. При возведении в куб:
- положительного
числа
получается … число;
- отрицательного числа
получается … число,
- 0, получается … .
1³=… (-1)³=… 0³=…
30. Запись выражения без скобок называется … скобок
Слайд 21
31. Если ху= 0,то имеем 3 случая:
1)
х=0, а у…0;
2) х…0, а у=0;
3) х…0 и
у…0.32.Реши уравнение:
1) 5х=0; 2) – 7х=0; 3) ах=0
Слайд 22
33. Если перед скобками стоит знак
+ , то
нужно
опустить … и … + , сохранив знаки слагаемых,
… в скобках;если первое … в скобках записано без …, то это … надо записать со знаком +.
а+(в-с)=…
а+(-в+с)=…
Слайд 23
34.Если перед скобками стоит знак
– , то
нужно
… знаки слагаемых, стоящих в скобках на …
;если первое … в скобках записано без …, то это … надо записать со знаком … .
а–(в–с)= …
а–(–в+с)=…
Слайд 31
Стр. 228, № 1304 (а,б,в)
Д.Р № 127,
на 05.04.18
а) (х +у –z)·3=3х+3у–3z
в) –8·(a – b
– c)=–8а+8b+8cб) 4·(т –п –р)=4т–4п–4р
Слайд 32 Оцените ДР: - все ответы верны и подробно
записано решение
«5» - все ответы верны и подробно записано решение, но допущены вычислительные ошибки «4» - ответы верны, но решение либо неполное, либо его нет совсем «3» -домашняя работа отсутствует- «2»
Слайд 34
Цели урока:
Ввести понятие «подобные слагаемые».
Учиться складывать подобные слагаемые.
Развивать письменную и устную математическую речь.
Слайд 36
Стр. 225,
№1281(в,г,д)
Письменно в тетради
в) а·(b – m
+ n)= Сколько слагаемых должно получиться в результате ?
Слайд 39
Стр. 225,
№1281(в,г,д)
Письменно в тетради
в) а·(b – m +
n)=аb–ат +ап 3 слагаемых
3 слагаемых
Слайд 45
Стр. 225,
№1281(в,г,д)
Письменно в тетради
г) –а·(6b –3c +4)=
= –а·6b
– (–а·3с)+ (–а·4)== – 6аb +3ас – 4а
Слайд 50
Стр. 225,
№1281(в,г,д)
Письменно в тетради
д) (3т –2k +1) ·(–3)=
=(3т·(–3))–(2k·(–3))+(1·(–3))=
Слайд 51
Стр. 225,
№1281(в,г,д)
Письменно в тетради
д) (3т –2k +1) ·(–3)=
=(3т·(–3))–(2k·(–3))+(1·(–3))=
=(–9т)–(–6k)+(–3)=
Слайд 52
Стр. 225,
№1281(в,г,д)
Письменно в тетради
д) (3т –2k +1) ·(–3)=
=(3т·(–3))–(2k·(–3))+(1·(–3))=
=(–9т)–(–6k)+(–3)=
= –9т+6k–3
Слайд 54
Стр. 225,
№1282(а,б,в,г)
С пояснением
Вынесение общего множителя за скобки
ас+вс =(а+в)·с
ас - вс =(а - в)·с
Слайд 55
Стр. 225,
№1282(а,б,в,г)
С пояснением
Вынесение общего множителя за скобки
ас+вс =(а+в)·с
ас - вс =(а - в)·са) 9·13+9·7=
письменно
Слайд 56
Стр. 225,
№1282(а,б,в,г)
С пояснением
Вынесение общего множителя за скобки
ас+вс =(а+в)·с
ас - вс =(а - в)·са) 9·13+9·7=
Слайд 57
Стр. 225,
№1282(а,б,в,г)
С пояснением
Вынесение общего множителя за скобки
ас+вс =(а+в)·с
ас - вс =(а - в)·са) 9·13+9·7=9·(13+7)=
Слайд 58
Стр. 225, №1282(а,б,в,г)
С пояснением
Вынесение общего множителя
за скобки
ас+вс =(а+в)·с ас - вс =(а - в)·с
а)
9·13+9·7=9·(13+7)=9·20=
Слайд 59
Стр. 225,
№1282(а,б,в,г)
С пояснением
Вынесение общего множителя за скобки
ас+вс =(а+в)·с
ас - вс =(а - в)·са) 9·13+9·7=9·(13+7)=9·20=180
б,в,г- устно
Слайд 60
Изучение нового материала
Назовите выражения с одинаковой буквенной частью
4а; -0,03авс; 7,2ва
-8ав; -ху; авс; 9авс;12а; -7ав; -авс; 3,1а
Слайд 62
Изучение нового материала
4а; -0,03авс; 7,2ва
-8ав; -ху; авс; 9авс;
12а; -7ав; -авс;
3,1аВыражения, имеющие одинаковую буквенную часть называются
подобными.
Слайд 63
Изучение нового материала
4а; -0,03авс; 7,2ва
-8ав; -ху; авс; 9авс;
12а; -7ав; -авс;
3,1аЧем могут отличаться
подобные выражения?
Слайд 64
Изучение нового материала
4а; -0,03авс; 7,2ва
-8ав; -ху; авс; 9авс;
12а; -7ав; -авс;
3,1аЧаще всего
подобные выражения будут рассматриваться как
слагаемые.
Слайд 66
Стр.225, №1283(а,г,ж)
Письменно
в тетради c пояснением
а) -9х+7х-5х+2х
Какими являются
слагаемые в данной сумме?Что надо сделать, чтобы их сложить?
Назовите коэффициенты.
Слайд 68
Стр.225, №1283(а,г,ж)
Письменно
в тетради c пояснением
а) -9х+7х-5х+2х=
= (-9+7-5+2)·х=
= (-14+9) ·х =
Слайд 69
Стр.225, №1283(а,г,ж)
Письменно
в тетради c пояснением
а) -9х+7х-5х+2х=
= (-9+7-5+2)·х=
= (-14+9) ·х = -5х
Слайд 70
Стр.225, №1283(а,г,ж)
Письменно
в тетради c пояснением
г) -3,8k-k+3,8k+k=
Какими являются
слагаемые в данной сумме?Что надо сделать, чтобы их сложить?
Назовите коэффициенты.
Слайд 74
Стр.225, №1283(а,г,ж)
Письменно
в тетради c пояснением
г) –3,8k–k+3,8k+k=
=(–3,8–1+3,8+1)·k=
0
0
Слайд 75
Стр.225, №1283(а,г,ж)
Письменно
в тетради c пояснением
г) –3,8k–k+3,8k+k=
=(–3,8–1+3,8+1)·k=
=0 ·k
=0
0
Слайд 76
Стр.225, №1283(а,г,ж)
Письменно
в тетради c пояснением
г) –3,8k–k+3,8k+k=
=(–3,8–1+3,8+1)·k=
=0 ·k
=00
0
Слайд 77
Стр.225, №1283(а,г,ж)
Письменно
в тетради c пояснением
Какими являются слагаемые в
данной сумме?Что надо сделать, чтобы их сложить?
Назовите коэффициенты.
Слайд 83
Итоги урока
3. Сложите
подобные слагаемые:
а) а+4а+7а=
б) –10а+5а –5а+10а=
в)
10а – в+ а + в=
Слайд 84
Итоги урока
Оцените свое настроение по итогам
