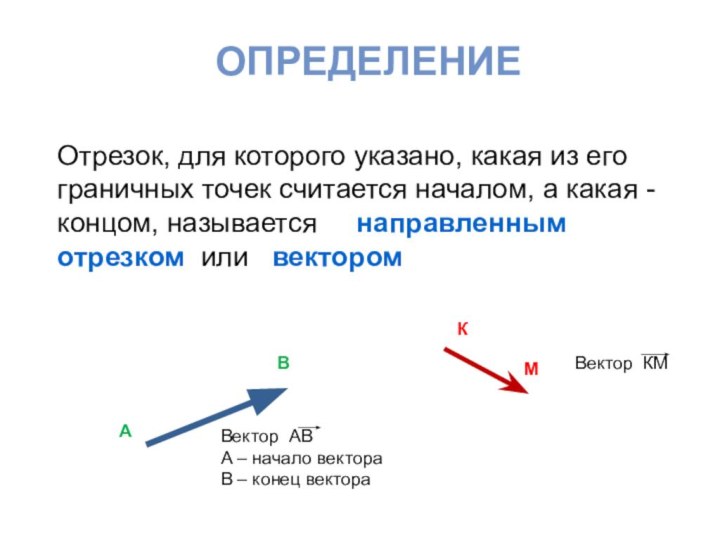
граничных точек считается началом, а какая - концом, называется
направленным отрезком или векторомА
В
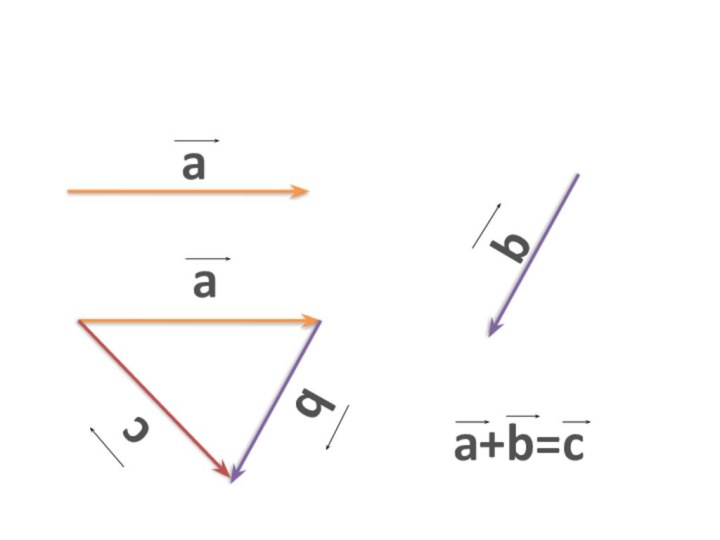
Вектор АВ
А – начало вектора
В – конец вектора
К
М
Вектор КМ
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

















А
В
Вектор АВ
А – начало вектора
В – конец вектора
К
М
Вектор КМ
с
К
Р
М
ОТКЛАДЫВАНИЕ ВЕКТОРА ОТ ДАННОЙ ТОЧКИ
F
Свойства:
Для любых чисел k, l и любых векторов а и в справедливы равенства
(kl)a=k(la) (сочетательный закон)
(k+l)а=ka+la (первый распределительный закон)
k(a+b)=ka+kb (второй распределительный закон)