Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике на тему Рационал теңдеулер мен рационал теңсіздіктер

Содержание

Сабақтың мазмұны.Рационал теңдеулерді шешу.Рационал теңдеуді көбейткіштерге жіктеу әдісімен шешу.Жаңа айнымалы енгізу әдісімен шешу.Рационал теңсіздіктерді шешу.
Сабақтың тақырыбы. Рационал теңдеулер мен рационал теңсіздіктер Сабақтың мазмұны.Рационал теңдеулерді шешу.Рационал теңдеуді көбейткіштерге жіктеу әдісімен шешу.Жаңа айнымалы енгізу әдісімен шешу.Рационал теңсіздіктерді шешу. Рационал теңдеулерді шешу.Егер Р пен Q көпмүшеліктер 2-мысал. Теңдеуді шешу керек: Шешуі: Теңдеуді түрге келтірейік: Бұл теңдеуді өзімен мәндес түрдегі теңдеумен алмастырамыз: Квадрат теңдеудің Көбейткіштерге жіктеу әдісі мынаған негізделген: егер түріндегі көбейтінді болса, онда Теңдеудің Теңдеулер жиынтығының да шешімі болады. Кері тұжырым, жалпы жағдайда дұрыс емес, яғни теңдеуді көбейткіштерге жіктеу әдісімен шешкенде теңдеулер жиынтығынан табылған түбірлердің тек 2-мысал. Теңдеуді шешу керек: деп алып теңдеудің сол жағын көбейткіштерге Теңдеуді жаңа айнымалы енгізу әдісімен шешу 1-мысал. Теңдеуді шешу керек: Шешуі: Бұл теңдеудің түбірлері: және Сонымен берілген теңдеу келесі теңдеулер жиынтығына мәндес екен:Бұл теңдеулердің түбірі жоқ.Жауабы: Рационал теңсіздіктерді шешу. 1-мысал. Теңсіздікті шешу керек: Шешуі: Рационал теңсіздіктер жүйелері мен жиынтықтарын шешу мысалдары 1-Мысал. Теңсіздіктер жүйесін шешу керек: Екінші теңсіздікті шешеміз: Бұдан теңсіздіктің шешімі (-8,8) болатыны көрінеді:Екі теңсіздіктің шешімдерін сан
Слайды презентации

Слайд 2 Сабақтың мазмұны.
Рационал теңдеулерді шешу.
Рационал теңдеуді көбейткіштерге жіктеу әдісімен

Сабақтың мазмұны.Рационал теңдеулерді шешу.Рационал теңдеуді көбейткіштерге жіктеу әдісімен шешу.Жаңа айнымалы енгізу әдісімен шешу.Рационал теңсіздіктерді шешу.

шешу.
Жаңа айнымалы енгізу әдісімен шешу.
Рационал теңсіздіктерді шешу.

Слайд 3 Рационал теңдеулерді шешу.
Егер Р пен Q

Рационал теңдеулерді шешу.Егер Р пен Q көпмүшеліктер болса, онда

көпмүшеліктер болса, онда

түріндегі теңдеуді рационал теңдеу деп атайды. Теңдеуді шешу теңдеуінің шартын қанағаттандыратын түбірлерін табуға алып келеді







=0



Слайд 4

1-мысал. Теңдеуді шешу керек:

1-мысал. Теңдеуді шешу керек:


­




Жауабы: x=3/2

Шешуі:

Слайд 5 2-мысал. Теңдеуді шешу керек:
Шешуі: Теңдеуді
түрге

2-мысал. Теңдеуді шешу керек: Шешуі: Теңдеуді түрге келтірейік:

келтірейік:

Слайд 6 Бұл теңдеуді өзімен мәндес
түрдегі теңдеумен алмастырамыз:

Бұл теңдеуді өзімен мәндес түрдегі теңдеумен алмастырамыз: Квадрат теңдеудің түбірлері


Квадрат теңдеудің түбірлері
және

Екінші шартты

қанағаттандырмайды,өйткені,

0

Ал

саны оны қанағаттандырады.

Жауабы: х=4

-8


Слайд 7
Көбейткіштерге жіктеу әдісі мынаған негізделген: егер
түріндегі

Көбейткіштерге жіктеу әдісі мынаған негізделген: егер түріндегі көбейтінді болса, онда Теңдеудің

көбейтінді болса, онда

Теңдеудің кез-келген шешімі





функциясы




теңдеуін көбейткіштерге жіктеу.

Слайд 8 Теңдеулер жиынтығының да шешімі болады. Кері тұжырым,
жалпы

Теңдеулер жиынтығының да шешімі болады. Кері тұжырым, жалпы жағдайда дұрыс емес,

жағдайда дұрыс емес, яғни
теңдеулер жиынтығының шешімдерінің әрбіреуі


теңдеуінің шешімі болмауы мүмкін.





Мысалы.

Теңдеулер жиынтығының шешімдері


Бірақ х=1 х=0 мәндері


Теңдеуінің түбірі бола алмайды

Слайд 9
теңдеуді көбейткіштерге жіктеу әдісімен шешкенде

теңдеуді көбейткіштерге жіктеу әдісімен шешкенде теңдеулер жиынтығынан табылған түбірлердің тек

теңдеулер жиынтығынан табылған түбірлердің тек
теңдеудің анықталу аймағында

жататындығы ғана

теңдеудің де түбірлері болады.

1-мысал. Теңдеуді шешу керек:


Шешуі: теңдеудің сол жағын көбейткіштерге жіктейміз.


Бірінші теңдеудің түбірі х=-2. Екінші теңдеудің түбірі жоқ.

Жауабы:-2

Слайд 10 2-мысал. Теңдеуді шешу керек:
деп

2-мысал. Теңдеуді шешу керек: деп алып теңдеудің сол жағын көбейткіштерге

алып теңдеудің сол жағын көбейткіштерге жіктеуге болар еді. Біз

теңдеудің
бүтін түбірін табуға мүмкіндік беретін таңдау әдісін көрсетеміз. Бүтін түбірдің
бар болуының қажетті шартын пайдаланып,бос мүшенің бөлгіштерін жазып
шығарамыз.

Шешуі:


мұнда


Енді іріктеуді бастаймыз. Берілген теңдеудегі х-тің орнына

қоямыз:

Демек, х=1 теңдеудің түбірі емес,
іріктеуді жалғастырамыз


Бұдан

теңдеудің түбірі болатынын көреміз.

көпмүшенің ‘x-2’-ге қалдықсыз бөлінетінін пайдаланамыз.

Енді

Слайд 11











Сонымен

олай болса бастапқы теңдеу мына
түрге ие болады:


Одан әрі,


Екінші теңдеудің түбірі жоқ

ал біріншіден х=2 аламыз.

Жауабы: х=2.

Слайд 12 Теңдеуді жаңа айнымалы енгізу әдісімен шешу
1-мысал. Теңдеуді

Теңдеуді жаңа айнымалы енгізу әдісімен шешу 1-мысал. Теңдеуді шешу керек: Шешуі:

шешу керек:
Шешуі: Бұл теңдеудің ерекшелігі- оның бірінші

коэффицентінің бос мүшеге
қатынасы,екінші коэффицентінің соңының алдындағы коэффиценттке
қатынасының квадратына тең:

Мұндай ерекшелігі бар теңдеуді
Қайтымды деп айтады.

Симметриялы теңдеулер қайтымды теңдеулердің дербес түрі. Қайтымды
теңдеулерді шешу әдісі симметриялы теңдеулерді шешу әдісіндей.
Теңдеудің екі жағын

-қа бөлеміз:



Енді

деп алсақ

болады. Бұларды

-теңдеуге қоямыз.

немесе

Слайд 13 Бұл теңдеудің түбірлері:
және
Сонымен берілген

Бұл теңдеудің түбірлері: және Сонымен берілген теңдеу келесі теңдеулер жиынтығына мәндес екен:Бұл теңдеулердің түбірі жоқ.Жауабы:

теңдеу келесі теңдеулер жиынтығына мәндес екен:

Бұл теңдеулердің түбірі жоқ.
Жауабы:

Слайд 14 Рационал теңсіздіктерді шешу.
1-мысал. Теңсіздікті шешу керек:

Рационал теңсіздіктерді шешу. 1-мысал. Теңсіздікті шешу керек: Шешуі: болғандықтан:


Шешуі:
болғандықтан:


Мұндағы функцияның нөлдер


үзіліс нүтелері жоқ. Сан өсіне

мен

мәндерін боялған дөңгелекшелермен белгілейміз де
жоғарыдағы схеманың 3n бойынша толқын тәрізді жүргіземіз.

Бұл суреттен теңсіздіктің шешімі

екенін көреміз.

Жауабы:

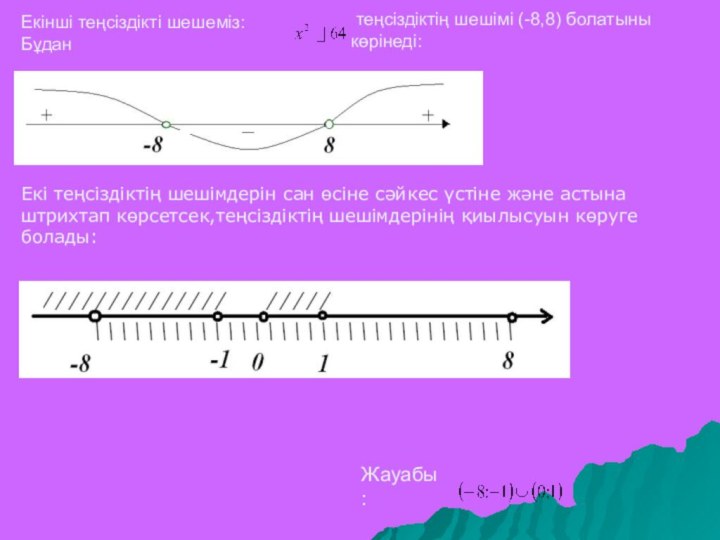
Слайд 15 Рационал теңсіздіктер жүйелері мен жиынтықтарын шешу мысалдары
1-Мысал.

Рационал теңсіздіктер жүйелері мен жиынтықтарын шешу мысалдары 1-Мысал. Теңсіздіктер жүйесін шешу

Теңсіздіктер жүйесін шешу керек:
Шешуі: Теңсіздіктерді жеке-жеке шешеміз

Сонымен,

теңсіздіктің шешімі:

.

  • Имя файла: prezentatsiya-po-matematike-na-temu-ratsional-teңdeuler-men-ratsional-teңsіzdіkter.pptx
  • Количество просмотров: 342
  • Количество скачиваний: 12
- Предыдущая плавание судов
Следующая - Презентация по информатике на темуОператоры присваивания, ввода и вывода

Похожие презентации

Презентация по математике, кроссворд-филворд. 6 класс. Можно использовать при проведение внеклассного мероприятия. Презентация по математике, кроссворд-филворд. 6 класс. Можно использовать при проведение внеклассного мероприятия. 158
Диаграммы и их применение в школьной практике Диаграммы и их применение в школьной практике 177
Замечательные кривые в математике Замечательные кривые в математике 157
Законы Арифметических действий Законы Арифметических действий 105
Натуральные числа. Подготовка к контрольной работе Натуральные числа. Подготовка к контрольной работе 161
Подобие треугольников Подобие треугольников 96
Математика в архитектуре и живописи Математика в архитектуре и живописи 146
Второй признак равенства треугольников Второй признак равенства треугольников 123
Дни недели и цвета радуги. методическая разработка по математике по теме Дни недели и цвета радуги. методическая разработка по математике по теме 134
Сложение и вычитание многозначных чисел Сложение и вычитание многозначных чисел 92
Проценты в нашей жизни Проценты в нашей жизни 109
Урок математики в 4 классе по теме Решение математических выражений, уравнений. презентация к уроку по математике (4 класс) по теме Урок математики в 4 классе по теме Решение математических выражений, уравнений. презентация к уроку по математике (4 класс) по теме 45
Противоположные числа Противоположные числа 106
В мире числовых суеверий В мире числовых суеверий 126
Шифры (7 класс) Шифры (7 класс) 146
Презентация к уроку Счёт в пределах 20 презентация к уроку по математике (1 класс) по теме Презентация к уроку Счёт в пределах 20 презентация к уроку по математике (1 класс) по теме 107
Признаки параллельности прямых Признаки параллельности прямых 175
Число і цифра 7 Число і цифра 7 105
Презентация по математике на тему: Основное свойство дроби (5 класс) Презентация по математике на тему: Основное свойство дроби (5 класс) 121
Дидактическая игра как один из методов обучения на уроках математики начальной школы презентация по математике по теме Дидактическая игра как один из методов обучения на уроках математики начальной школы презентация по математике по теме 119
Измерения, погрешности и точности Измерения, погрешности и точности 117
ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА (9 КЛАСС) ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА (9 КЛАСС) 114
Нод по познавательному развитию (ФЭМП) Сказка Теремок план-конспект занятия по математике (средняя группа) Нод по познавательному развитию (ФЭМП) Сказка Теремок план-конспект занятия по математике (средняя группа) 110
Урок математики Умножение на 1 и на 0, 3 класс, ФГОС, Школа России план-конспект урока по математике (3 класс) Урок математики Умножение на 1 и на 0, 3 класс, ФГОС, Школа России план-конспект урока по математике (3 класс) 228
Движения Движения 130
Конспект урока с презентацией по математике Проценты (5 класс) Конспект урока с презентацией по математике Проценты (5 класс) 124
Витаминный коктейль. Подготовка к ЕГЭ Витаминный коктейль. Подготовка к ЕГЭ 98
Решение составных задач презентация к уроку по математике по теме Решение составных задач презентация к уроку по математике по теме 125
урок математики во 2 классе УМК Перспективная начальная школа план-конспект урока по математике (2 класс) урок математики во 2 классе УМК Перспективная начальная школа план-конспект урока по математике (2 класс) 129
округление чисел до указаного розряда округление чисел до указаного розряда 97