- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Отношения и пропорции 6 класс
Содержание
- 3. « Я слышу- я забываю,Я вижу –
- 4. Цель:Узнать что такое пропорции и отношения. Понять прямая и обратная пропорциональные зависимости.
- 5. Отношения2:10=0,2 Отношение 2к10 равно 0,239:3=13Отношение 39к3 равно 13
- 6. На самом деле что же такое отношения?Отношения
- 7. Что показывает отношение двух чисел?Оно показывает во
- 8. ЗадачаКакую часть урока занимала самостоятельная работа ,
- 9. Пропорции20:4=0,5:0,15=5
- 10. Слово «пропорция» (от латинского propotio) означает «соразмерность»,
- 11. Верная и неверная пропорции.1,5:3=2,5:50,5=0,5Верная пропорция7:2=12,8:43,5 ? 3,2Неверная пропорция
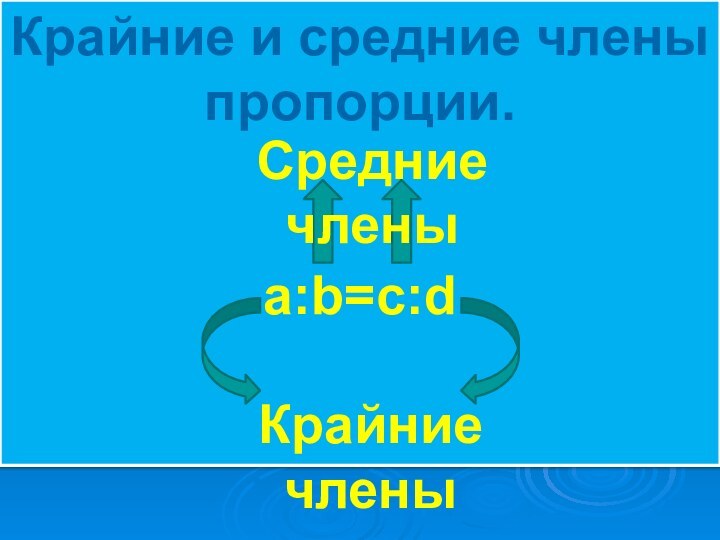
- 12. Крайние и средние члены пропорции.a:b=c:dСредние членыКрайние члены
- 13. Основное свойство пропорции.В верной пропорции произведение крайних
- 14. Имеется ещё одно свойство! Если в верной
- 15. Золотым сечением и даже «божественной пропорцией» называли
- 16. Золотое сечение в архитектуре Перенесемся теперь в
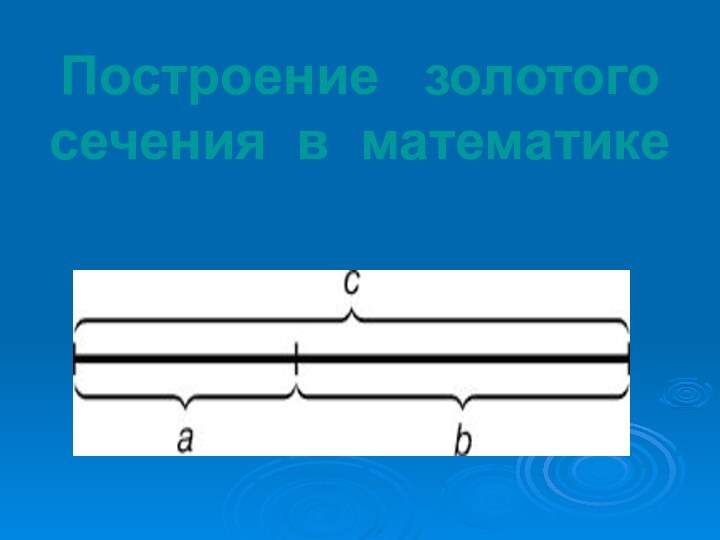
- 17. Построение золотого сечения в математике
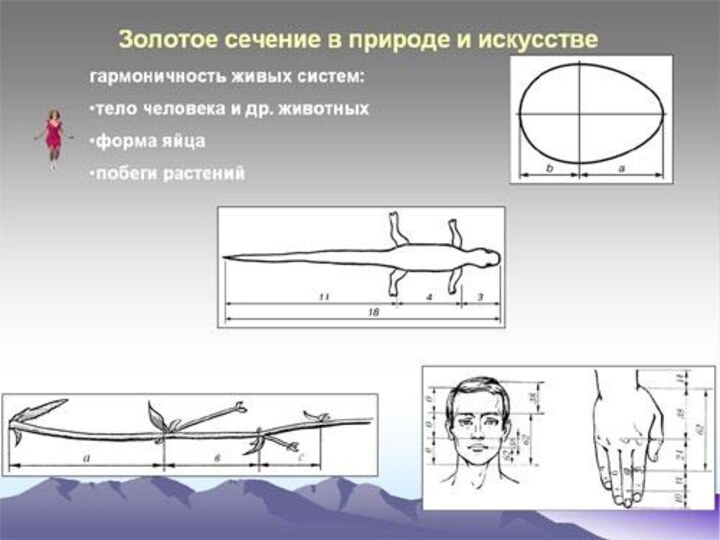
- 18. Золотое сечение в изобразительном искусстве
- 20. Число «пи» Произносится «пи») — математическая константа,
- 21. Длина окружности больше её диаметра примерно в П = 3.1415…
- 22. Сегодня исполняется ровно 250 лет с того
- 23. На первый взгляд, что здесь такого важного?
- 24. История Символ константыВпервые обозначением этого числа греческой
- 25. История числа π шла параллельно с развитием
- 26. Свойствоπ — иррациональное число, то есть его
- 27. π — трансцендентное число, то есть оно
- 28. Известно много формул числа π:Франсуа Виет:Формула Валлиса:Ряд
- 29. Решаем устно!1.Найдите не верную пропорцию: А)18:6=24:8
- 30. Прямая и обратная пропорциональные зависимости.3,2:1,5=115,2:xX=1,5*115,2:3,2=54Ответ:54.
- 31. На самом деле что же такое прямая
- 32. Задача!Для варки варенья из вишни на 6
- 33. Найдите длины сторон четырехугольника, если они пропорциональны
- 34. В 35 г пюре содержится 35 x
- 35. 1 площадь поля 80 га. Кукурузой засеяли
- 36. Маленькое колесо повозки имеющая окружность 2,4 м
- 37. МасштабМасштаб – отношение длины
- 38. Особенности масштаба! Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта.
- 39. 1 : 100 Линейный масштаб представляет собой линию разделенную на равные отрезки.Виды масштаба.1) Линейный.2)Численный.
- 40. Задача на масштаб.Расстояние между г.Кемерово и Москва
- 41. Скачать презентацию
- 42. Похожие презентации






































Слайд 4
Цель:
Узнать что такое пропорции и отношения.
Понять прямая
и обратная пропорциональные зависимости.
Слайд 6
На самом деле что же такое отношения?
Отношения –
это частное двух чисел . Оно показывает во сколько
одно число больше второго , или какую часть одно число составляет от второго
Слайд 7
Что показывает отношение двух чисел?
Оно показывает во сколько
раз первое число больше второго , или какую часть
первое число составляет от второго.
Слайд 8
Задача
Какую часть урока занимала самостоятельная работа , которая
длилась 20 минут , если продолжительность урока 45 минут?
20/45=4/9=0,44=44%
Ответ:
самостоятельная работа занимает 44%урока.Слайд 10 Слово «пропорция» (от латинского propotio) означает «соразмерность», определённое
соотношение частей между собой.
В математике: Равенство двух отношений.
На самом деле что же такое пропорция?
Слайд 11
Верная и неверная пропорции.
1,5:3=2,5:5
0,5=0,5
Верная пропорция
7:2=12,8:4
3,5 ? 3,2
Неверная пропорция
Слайд 13
Основное свойство пропорции.
В верной пропорции произведение крайних членов
равно произведению средних.
Признак : Если произведение крайних равно
произведению средних членов , то пропорция верна
Слайд 14
Имеется ещё одно свойство!
Если в верной пропорции
поменять местами средние и крайние члены , то получившиеся
новые пропорции тоже верны. 1)a:b=c:d
d:b=c:a
2)a:b=c:d
a:c=b:d
3)d:c=b:a
3:4=6:8
8:4=6:3
3:6=4:8
8:6=4:3
Слайд 15 Золотым сечением и даже «божественной пропорцией» называли математики
древности и средневековья деление отрезка, при котором длинна всего
отрезка так относится к длине его большей части, как длинна большей части к меньшей. Приближенно это отношение равно 0, 618 ≈5/8. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается и в природе.Золотое сечение
Слайд 16
Золотое сечение в архитектуре
Перенесемся теперь в эпоху
классической Греции. Великолепные памятники архитектуры оставили нам зодчие древней
Греции. И среди первое место по праву принадлежит Парфенону. Храм Афины - Парфенон был построен в честь победы эллинов над персами. Для создания гармонической композиции на холме его строители даже увеличили холм в южной части, соорудив для этого мощную насыпь .
Слайд 20
Число «пи»
Произносится «пи») — математическая константа, выражающая
отношение длины окружности к длине её диаметра. Обозначается буквой
греческого алфавита «пи». Старое название — лудольфово число.Слайд 22 Сегодня исполняется ровно 250 лет с того дня,
как немецкий физик и математик Иоганн Генрих Ламберт, отвлёкшись
от своих трактатов по оптике и астрономии, доказал, что Пи является иррациональным числом. Это значит, что не существует таких целых чисел p и q, для которых было бы верно равенство Пи = p/q.История
Слайд 23 На первый взгляд, что здесь такого важного? Рациональное
число или иррациональное — какая разница? В практическом инженерном
применении это ничего не меняет, потому что при конструкции любого цилиндра или хирургической иголки они всё равно аппроксимируют Пи с погрешностью, допустимой для каждой конструкции. Это могли делать инженеры Римской империи почти так же успешно, как мы, оснащённые мощной компьютерной техникой (хотя у Пифагора, например, понятие иррациональных чисел вызывало столь сильное отвращение, что он вообще отрицал их существование).История
Слайд 24
История
Символ константы
Впервые обозначением этого числа греческой буквой
воспользовался британский математик Джонс в 1706 году, а общепринятым
оно стало после работ Леонарда Эйлера в 1737 году.Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.
Слайд 25 История числа π шла параллельно с развитием все
геометрии
й математики. Некоторые авторы разделяют весь процесс на 3
периода: древний период, в течение которого π изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке, и эра цифровых компьютеров.История
Слайд 26
Свойство
π — иррациональное число, то есть его значение
не может быть точно выражено в виде дроби m/n,
где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа π была впервые доказана Иоганном Ламбертом в 1761 году путём разложения числа в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел π и π2.Слайд 27 π — трансцендентное число, то есть оно не
может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность
числа π была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году.Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа π, то доказательство трансцендентности π положило конец спору о квадратуре круга, длившемуся более 2,5 тысяч лет.
Свойство
Слайд 28
Известно много формул числа π:
Франсуа Виет:
Формула Валлиса:
Ряд Лейбница:
Тождество
Эйлера:
Т. н. «интеграл Пуассона» или «интеграл Гаусса»
Интегральный синус:
Выражение через
полилогарифм:Соотношения
Слайд 29
Решаем устно!
1.Найдите не верную пропорцию: А)18:6=24:8
В)30:5=42:7 Б)36:9=50:10 Г)63:9=28:4
2.Назовите крайние и
средние члены пропорций(из задания 1)Слайд 31 На самом деле что же такое прямая и
обратная пропорциональная зависимости?
Прямая пропорциональная зависимость – это две величины
, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) в столько же раз.Обратная пропорциональная зависимость-это две величины , если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается(увеличивается)во столько же раз.
Слайд 32
Задача!
Для варки варенья из вишни на 6 кг
ягод берут 4 кг сахарного песку . Сколько сахарного
песку надо взять на:1)12 кг ягод? 2) 3 кг ягод?Решение:
6 кг ягод – 4кг песку
12 кг ягод – х кг песку
х = 12*4/6=8(кг)-надо взять;
Ответ:8кг.
6кг ягод-4кг песку
3кг ягод-х кг песку
х = 3*4/6=2(кг)-надо взять;
Ответ:2кг.
Слайд 33 Найдите длины сторон четырехугольника, если они пропорциональны числам
1, 3, 3 и 5, а самая длинная сторона
больше самой короткой на 12 см.х - самая короткая сторона
х + 12 - самая длинная сторона,
а также
остальные стороны 3х, 3х, и последняя 5х, то есть
х + 12 = 5х
4х = 12
х = 3 - самая короткая сторона четырехугольника
3*3 = 9 вторая и третья
3*5 = 15 самая длинная сторона.
ЗАДАЧА
Слайд 34 В 35 г пюре содержится 35 x 0,08
= 2,8 г воды и 35 – 2,8 =
32,2 г сухого вещества.Добавим в пюре х грамм воды, тогда всего пюре станет (35 + х) г, воды в нем – (2,8 + х) г
Заметьте, что сухого вещества останется по-прежнему 32,2 г.
Составим пропорцию:
35 + x = 100%
2,8 + x = 86%
Решим пропорцию: (35 + x) x 86=(2,8 + x) x 100.
Получим: 3010 + 86x = 280 + 100x; 2730 = 14x; x = 195
Сколько надо добавить воды (в граммах) к 35 г сухого картофельного пюре с содержанием 8% воды, чтобы получить пюре с содержанием 86% воды?
1) 195 г;
2) 250 г;
3) 215 г;
4) 230 г.
Слайд 35 1 площадь поля 80 га. Кукурузой засеяли 45%
всей площади. Сколько гектаров поля засеяно кукурузой
80/100 * 0.45
= 0.36 -то есть засеяно кукурузой 36 га ЗАДАЧА
Слайд 36 Маленькое колесо повозки имеющая окружность 2,4 м обернулось
на некотором расстоянии 1250 раз. Сколько раз обернулось на
этом расстоянии0 большое колесо имеющая окружность 3мЗадача
1/2,4 — 1250 раз
1/3 — ? раз
Из пропорции получится 1000 оборотов
Можно и без пропорции, расстояние равно 2,4 м (на один оборот)* 1250(оборотов)=3000 м (всего)
3000 м / 3 м = 1000
Слайд 37
Масштаб
Масштаб – отношение длины отрезка
на карте к длине соответствующего отрезка на местности .
Масштаб бывает : числовой, линейный.Масштаб (нем. MaВstab, букв. «мерная палка»: MaВ «мера», Stab «палка») — в общем случае отношение двух линейных размеров.
Слайд 38
Особенности масштаба!
Во многих областях практического применения масштабом
называют отношение размера изображения к размеру изображаемого объекта.
Слайд 39
1 : 100
Линейный масштаб представляет собой линию
разделенную на равные отрезки.
Виды масштаба.
1) Линейный.
2)Численный.
Слайд 40
Задача на масштаб.
Расстояние между г.Кемерово и Москва равно
3000 км
Масштаб 1 : 20 000 000
Решение:
1 :
20 000 000 = х : 300 000 000 Х=15см.
Расстояние между городами Кемерово и Москва на карет равно 15 см на карте.
Ответ: 15 см.