владеют старшеклассники МОБУ Гимназия №2 с. Бураево и используют
в решении» .Методы исследования:
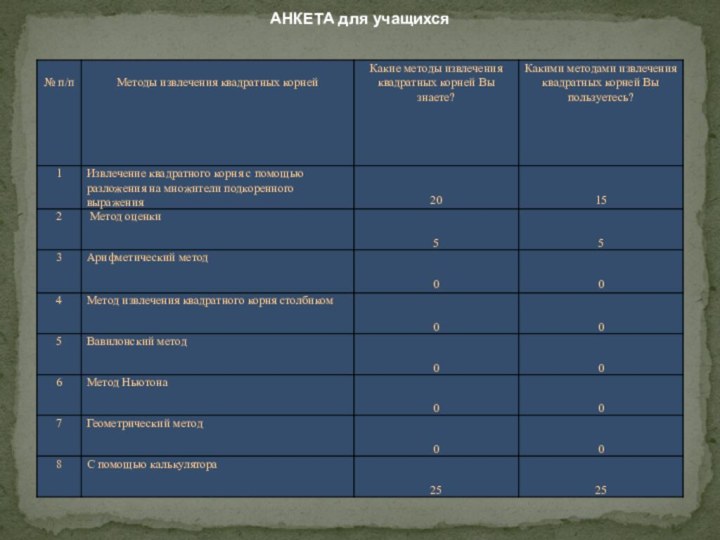
анкетирование,
сбор информации,
анализ.
Решая математическую задачу часто выбирают метод ее решения, которым лучше владеет решающий.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




















Решая математическую задачу часто выбирают метод ее решения, которым лучше владеет решающий.
Актуальность: владение методами извлечения квадратных корней сокращает время для выполнения задания, от которого зависит результат выполнения работы, процесса обучения.
Цель работы – сопоставление различных способов приближенного извлечения квадратных корней, выявление наиболее эффективного способа в зависимости от поставленной задачи.
Правильному применению методов можно научиться, только применяя их на разнообразных примерах.
Г. Цейтен
ЦЕЛИ И ЗАДАЧИ РАБОТЫ
Rx
r
Праздник отмечается девять раз в столетие:
1 января хх01 года 2 февраля хх04 года
3 марта хх09 года 4 апреля хх16 года
5 мая хх25 года 6 июня хх36 года
7 июля хх49 года 8 августа хх64 года
9 сентября хх81 года
Основатель праздника - школьный учитель Рон Гордон из Калифорнийского города Редвуд Сити в США.
Впервые этот праздник отмечался 9 сентября 1981 года (09-09-81).
Пример 1. Вычислить .
Решение. Шаг № 1 - ограничение корней. Определяем между какими
числами кратными десяти расположен корень данного числа.
Шаг № 2 - отсев лишних чисел.
Шаг № 3 – финальные вычисления.
= 58.
Вычитать нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю.
Подсчитать количество выполненных действий – это число есть целая часть числа извлекаемого квадратного корня.
Алгоритм извлечения квадратного корня арифметическим способом
ВАВИЛОНСКИЙ МЕТОД
Пример 2: вычислить
Результат извлечения корня с помощью калькулятора равен 5,292.
3. Находим среднее арифметическое чисел х и у, которое и будет приближенным значением квадратного корня из числа А.
4. Повторяя процесс несколько раз, достигается необходимая точность приближения.
В ходе решения многих математических задач приходится оперировать с квадратными корнями. Представленные методы позволят всем, кто заинтересуется данной темой, овладеть навыками вычисления квадратного корня, использовать при решении задач и не зависеть от наличия в кармане калькулятора.