- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему проекта по математике 5 класс Приближенные вычисления в нашей жизни
Содержание
- 2. Цели и задачи.
- 3. Округление — математическая операция, позволяющая уменьшить количество
- 4. Правила округления.Если число округляют до какого–нибудь разряда,
- 5. Виды округления.Помимо математического существуют ещё и другие
- 6. 3) округление к меньшему, если у числа
- 7. Магазины часто выставляют «некруглые» цены (например, вместо
- 8. Тоже самое может быть при оплате за
- 10. Вопрос и решение:Вопрос: Сколько рублей переплатит семья
- 11. Вычислив разность полученного результататарифного плана « 01
- 12. Вот ещё одна задача: Одна деталь имеет
- 13. Решение:1 способ.Сначала мы узнаем общую массу этих
- 14. Вывод: В этой задаче точнее будет результат первого способа.
- 15. Кроме того, выполнение измерения также вводит неточности. Мы измеряли ширину улицы.
- 16. Мера, метр, отложилась в ее ширине, допустим,
- 17. Если бы мы пожелали измерить ширину улицы
- 18. При еще более тщательном измерении мы учтём
- 19. Арифметика приближенных чисел не во всем сходна
- 20. длина которого 68 м, а ширина —
- 21. Но числа 68 и 42 не точные,
- 22. Выполнение действия видно из следующей схемы:
- 23. Можно решить ещё вот такую задачу:Для ремонта
- 24. Решение:Р = ( 4.4 + 2,8) *
- 25. Площадь двери = 2*0.8 = 1.6 квадратных метров.
- 26. Площадь окна = 1.46 * 1.5 = 2.19 квадратных метров.
- 27. Теперь узнаем площадь оклеиваемой поверхности. Чтобы это
- 28. Погрешность весов.Весы являются измерительным инструментом и предназначены
- 29. Погрешность весов бывает от 5 грамм и более.
- 30. Масса нетто - это масса продуктов без
- 31. Часто используется, например, для указания:пределов изменения каких-либо
- 32. Чаще всего при округлении бывают погрешности.Например: изготовить
- 33. «Нечестно писать больше цифр, чем
- 34. Скачать презентацию
- 35. Похожие презентации
Цели и задачи. Задачи:Изучить соответствующую литературу; Выбрать нужный материал; Проанализировать и обобщить материал. Цель: знакомство с приближенными вычислениями и точными значениями.

































Слайд 2
Цели и задачи.
Задачи:
Изучить
соответствующую литературу;
Цель: знакомство с приближенными вычислениями и точными значениями.Слайд 3 Округление — математическая операция, позволяющая уменьшить количество знаков
в числе за счёт замены числа его приближённым значением
с определённой точностью.
Слайд 4
Правила округления.
Если число округляют до какого–нибудь разряда, то
все следующие за этим разрядом цифры заменяют нулями, а
если они стоят после запятой, то их отбрасывают.Если первая отброшенная или заменяемая нулём цифра равна 5, 6, 7, 8, 9, то стоящую перед ней цифру увеличивают на 1.
Если первая отброшенная или заменяемая нулём цифра равна 0,1,2,3,4,то стоящую перед ней цифру оставляют без изменения. И нули в конце отбрасываются.
Если целая часть – трёхзначное число, то после округления оно должно остаться трёхзначным. Четырёхзначное- четырехзначным и т.д.
Слайд 5
Виды округления.
Помимо математического существуют ещё и другие виды
округления:
1) банковское — округление половины к ближайшему чётному числу.
В этом случае исчезает систематическая ошибка округления при суммировании большого количества чисел.2) округление к большему, если у числа округляемые знаки не равны нулю, число округляется в большую сторону. Эту форму округления используют при расчётах с потребителями сотовые операторы связи, провайдеры интернет, в магазине.
Слайд 6 3) округление к меньшему, если у числа округляемые
знаки не равны нулю, то число округляется в меньшую
сторону.4) ненулевое округление — округление производится согласно правилам математического округления, однако если округляется ненулевое число, результатом округления которого должен стать 0, округление производится «от нуля».
Слайд 7 Магазины часто выставляют «некруглые» цены (например, вместо 100
руб. пишут 99 руб.). Это делается как для создания
у покупателя впечатления более низкой цены, так и для стимулирования покупателей оставлять чаевые.Слайд 8 Тоже самое может быть при оплате за домашний
телефон.
Рассмотрим это на примере задачи:
В день семья сделала 7
звонков. Сын звонил своим друзьям, мама звонила на работу, папа заказывал пиццу, бабушка звонила своей сестре, дочка звонила подружке узнать уроки, потому что её не было в школе, а дедушка звонил в аптеку, чтобы узнать - не привезли ли ещё ему новых лекарств, но как обычно он с первого раза ничего не расслышал и ему пришлось перезванивать. В среднем звонки длились по четыре целых и несколько сотых минут. АТС округлила каждый звонок до 5 минут. И в среднем все звонки в день вместе длились 35 минут.
Тарифный план « 01 Повременная система»: предоставление абонентской линии 158 рублей, стоимость 1 минуты разговора 32 копейки, тарифный план «безлимитный» 378 рублей.
Слайд 10
Вопрос и решение:
Вопрос: Сколько рублей переплатит семья за
этот день? Узнать переплату за месяц. Решить задачу, рассматривая
тарифные планы « 01 Повременная система» и « 01 Абонентская плата, тариф – безлимитный». Найти наиболее выгодный тарифный план для данной семьи.Решение: Так как все говорили по четыре целых и несколько сотых минут, мы скажем, что они все говорили приблизительно 4,13 минут. Узнаем, сколько говорили все. Получилось 28,91 минут. АТС округлило это до 35 минут. Узнаем, сколько стоит разговор семьи без округления и с округлением. Получилось 9,2512 рублей без округления и 11,2 рублей с округлением.
Найдём погрешность: 11,2-9,2512=1,9488
Получилось, приблизительно 2 рубля переплатила семья за 1 день. А за месяц переплата составит-60 рублей.
11,2*30=336-за разговоры в месяц; прибавим 158 рублей за предоставление абонентской линии, в результате получим 494 рубля.
Слайд 11
Вычислив разность полученного результата
тарифного плана « 01 Повременная
система» и «01 Абонентская плата – тариф безлимитный»
494 -
378=116, можно сделать вывод:наиболее выгодный тарифный план для данной семьи «01 Абонентская плата – тариф безлимитный».
Слайд 12
Вот ещё одна задача:
Одна деталь имеет массу 13,26
кг, вторая- 14,43 кг, третья- 1,66 кг, а четвёртая-
15,875 кг.Вопрос:
Найдите общую массу этих четырёх деталей и округлите результат до десятых долей кг. Сравните ответ с результатом, полученным, если сначала округлить данные задачи до десятых долей, а потом её решить.
Слайд 13
Решение:
1 способ.
Сначала мы узнаем общую массу этих четырёх
деталей. У нас получилось 45,225 кг.
Теперь округлим это
число до десятых долей. Получилось примерно 45,2 кг.Затем можно узнать погрешность. Для этого мы из 45,225 кг вычтем приближённое значение с недостатком, это число 45,2 кг. Получилось 0,025 кг- это и есть погрешность.
2 способ.
Сначала мы округлим данные значения до десятых долей. У нас должно получиться так:
1 деталь- 13,3кг 3 деталь- 1,7кг
2 деталь- 14,4кг 4 деталь- 15,9кг
Теперь произведём сложение этих чисел. Получилось 45,3 кг.
После узнаем погрешность. Для этого из числа 45,225 вычтем приближённое значение- это число 45,3 кг. Получилось 0,075 кг - это и есть погрешность.
Слайд 16 Мера, метр, отложилась в ее ширине, допустим, 13
раз, и еще остался кусочек меньше метра. Мы можем
сказать, что ширина улицы 13 метров; на самом деле, однако, она равна 13 целым метрам и еще некоторому числу десятых, сотых и т. д. долей метра, которых мы не учли. Следовательно, результат нашего измерения можно изобразить так:ширина улицы = 13, ??? метра,
где вопросительные знаки означают неизвестные нам цифры десятых, сотых и т. д. долей.
Слайд 17 Если бы мы пожелали измерить ширину улицы точнее,
мы узнали бы, сколько в остающемся кусочке содержится дециметров
(десятых долей метра). Допустим, что дециметров содержится 8 и еще имеется некоторый остаток, меньший дециметра. Результат нового измерения, 13,8 м, будет точнее предыдущего, но и он не строго точен, потому что, кроме 8 десятых метра, в ширине улицы заключается еще некоторое неизвестное нам число сотых, тысячных и т. д. долей метра. Следовательно, полученный сейчас более точный результат мы можем выразить так:13,8?? метра.
Слайд 18 При еще более тщательном измерении мы учтём сотые
доли метра (сантиметры) в откинутом остатке, но пренебрежём остатком,
меньшим сантиметра; значит, и этот результат не будет безусловно точен. Вообще, как бы аккуратно мы ни мерили, мы никогда не можем быть твердо уверены, что далее последней полученной нами цифры не находятся еще другие, нам неизвестные.Дело, конечно, нисколько не меняется от того, что при измерениях остатки, большие половины единицы меры, обычно считаются за целые. Если бы при первом измерении улицы мы считали ее ширину не 13 метров, а 14,— это также был бы лишь приближенный результат. Его можно было бы выразить так:
14,??? метров,
где вопросительные знаки означают отрицательные цифры (т. е. показывают, на сколько десятых, сотых и т. д. долей число 14 больше истинной ширины улицы).
Итак, результат даже самого тщательного измерения не может быть рассматриваем как совершенно точный: он выражает истинную величину лишь более или менее приближенно. Такие числа называются приближенными.
Слайд 19 Арифметика приближенных чисел не во всем сходна с
арифметикой чисел точных. Покажем это различие на примере.
Пусть
требуется вычислить площадь прямоугольного участка.Слайд 20 длина которого 68 м, а ширина — 42
м. Если бы числа 68 и 42 были точные,
площадь участка в точности равнялась бы68 * 42 = 2856 кв. м.
Слайд 21 Но числа 68 и 42 не точные, а
приближенные: в длине не ровно 68 м, а немного
больше или меньше, так как невероятно, чтобы метр укладывался в ней в точности 68 раз. Да и сама длина метровой линейки едва ли в точности была равна 1 м. Мы можем, согласно предыдущему, выразить длину участка в метрах так:68,?
Подобным же образом и ширину участка выразим через
42,?
Проделаем теперь умножение приближенных чисел:
68,? * 42,?
Слайд 22
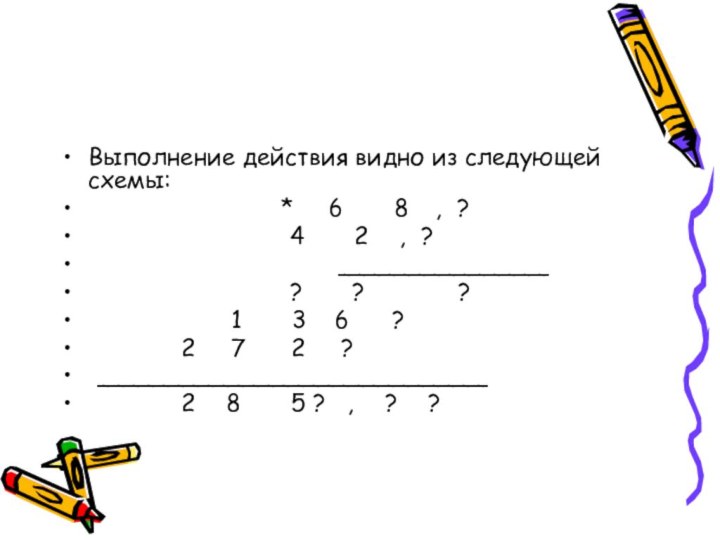
Выполнение действия видно из следующей схемы:
* 6 8 , ?
4 2 , ?
______________
? ? ?
1 3 6 ?
2 7 2 ?
__________________________
2 8 5 ? , ? ?
Слайд 23
Можно решить ещё вот такую задачу:
Для ремонта комнаты
семья решила поклеить
обои на стену. Они хотят узнать
сколько им потребуется обоев.
Слайд 24
Решение:
Р = ( 4.4 + 2,8) * 2
= 14.4 метра- периметр комнаты.
S = 14.4*3 = 43.2
квадратных метров -площадь стен в комнате.Слайд 27 Теперь узнаем площадь оклеиваемой поверхности. Чтобы это узнать,
надо из площади стен в комнате вычесть сумму площадей
окна и двери. Получилось 39.41 квадратного метра.Потом узнаем площадь обоев с размерами:
Ширина- 0.53 метра
Длина – 10 метров плюс минус 0.05 метра, приблизительно 10 метров.
Площадь равна 0.53 * 10 = 5.3 квадратных метров.
Теперь узнаем количество рулонов. Для этого площадь оклеиваемой поверхности разделим на площадь одного рулона обоев. Получилось приблизительно 8 рулонов.
Слайд 28
Погрешность весов.
Весы являются измерительным инструментом и предназначены для
измерения веса. Единицей измерения веса является килограмм, а также
его производные грамм, тонна, миллиграмм и т.д. Поскольку абсолютно точно вес измерить невозможно, то показания весов могут считаться достоверными с определенной погрешностью измерения.
Слайд 30
Масса нетто - это масса продуктов без упаковки.
Масса
брутто – это масса с упаковкой.
Знак плюс-минус (±)
— математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и отрицательным.
Слайд 31
Часто используется, например, для указания:
пределов изменения каких-либо параметров;
инструментальной
точности измерения физической величины;
ожидаемого разброса значений статистически измеренного параметра;
интервала
значений результата в приближённых математических вычислениях.
Слайд 32
Чаще всего при округлении бывают погрешности.
Например: изготовить совершенно
точные метровые линейки,
килограммовую гирю,
литровую кружку
чрезвычайно трудно.





























