- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Перпендикуляр и наклонная
Содержание
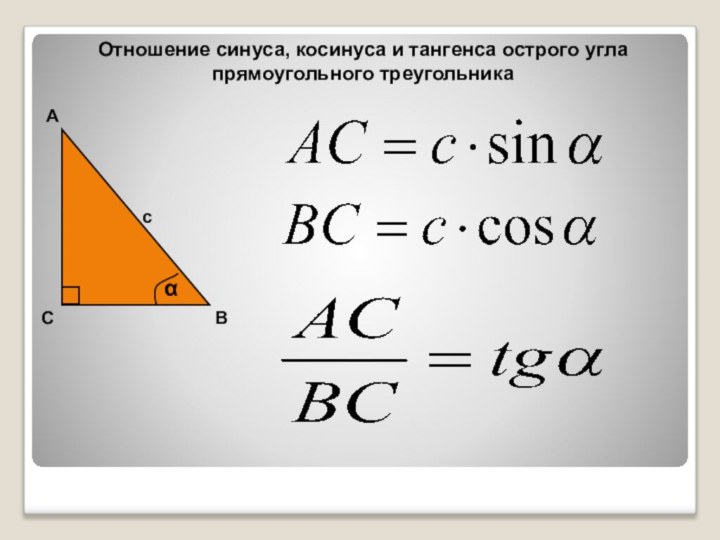
- 2. Отношение синуса, косинуса и тангенса острого угла прямоугольного треугольникаαсАСВ
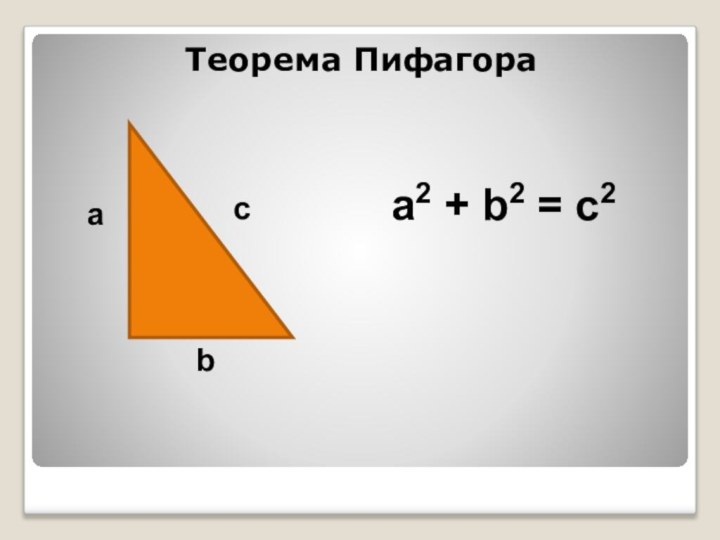
- 3. Теорема Пифагораabca2 + b2 = c2
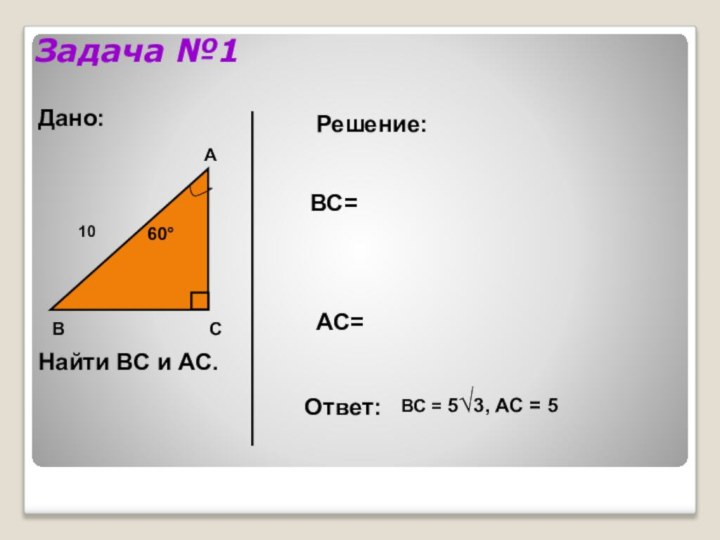
- 4. Задача №1ВАС60°10Дано:Найти ВС и АС.Решение:ВС=АС=Ответ:BC = 5√3, AC = 5
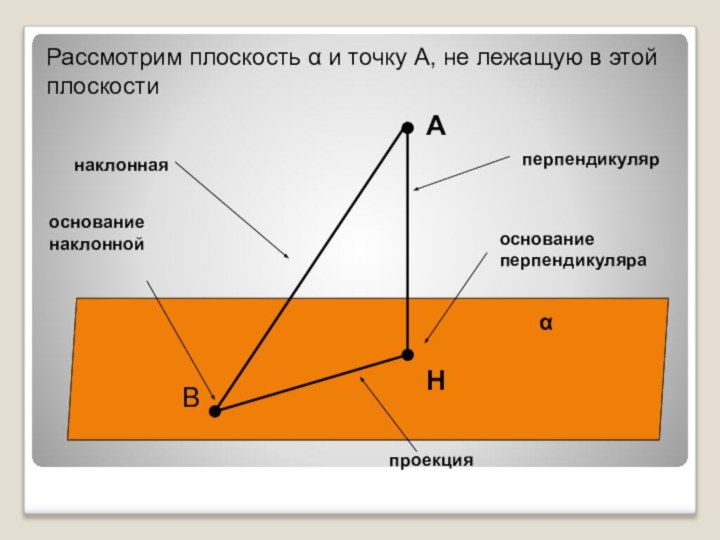
- 5. АαНперпендикуляроснование перпендикуляраРассмотрим плоскость α и точку А, не лежащую в этой плоскостиВнаклоннаяоснование наклоннойпроекция
- 6. Отрезок, проведенный через точку А перпендикулярно плоскости, называется ПЕРПЕНДИКУЛЯРОМ, опущенным из данной точки на плоскость.
- 7. Отрезок, соединяющий точку А с любой точкой плоскости, называется НАКЛОННОЙ.
- 8. Отрезок, соединяющий основание перпендикуляра и основание наклонной, называется ПРОЕКЦИЕЙ наклонной.
- 9. Задача №2Дано:αAD ┴α, AB, AC - наклонныеАB
- 10. Задача №3Решение:Дано:АВ – наклоннаяРасстояние от точки В
- 11. Задача №4Решение:Дано:α, АВ – отрезок не принадлежащий
- 12. Скачать презентацию
- 13. Похожие презентации
Отношение синуса, косинуса и тангенса острого угла прямоугольного треугольникаαсАСВ






Слайд 5
А
α
Н
перпендикуляр
основание перпендикуляра
Рассмотрим плоскость α и точку А, не
лежащую в этой
плоскости
В
наклонная
основание наклонной
проекция
Слайд 6 Отрезок, проведенный через точку А перпендикулярно плоскости, называется
ПЕРПЕНДИКУЛЯРОМ, опущенным из данной точки на плоскость.
Слайд 8 Отрезок, соединяющий основание перпендикуляра и основание наклонной, называется
ПРОЕКЦИЕЙ наклонной.
Слайд 9
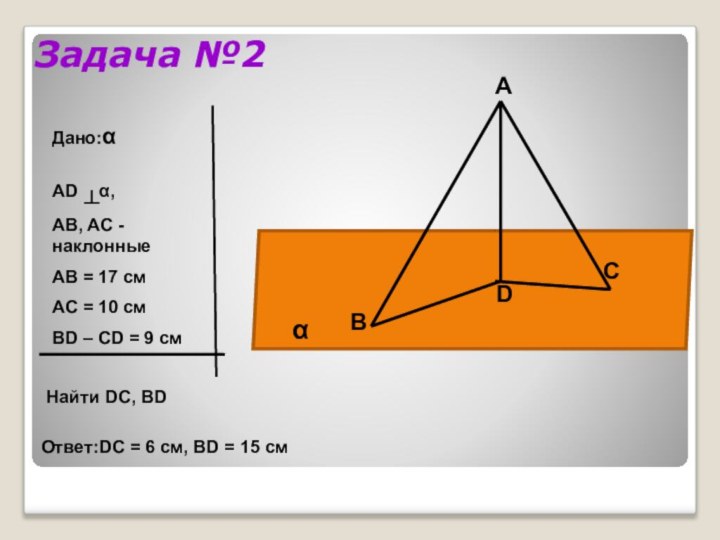
Задача №2
Дано:α
AD ┴α,
AB, AC - наклонные
АB =
17 см
АC = 10 см
BD – CD = 9
см Найти DС, BD
Ответ:DC = 6 см, BD = 15 см
A
B
C
D
α
Слайд 10
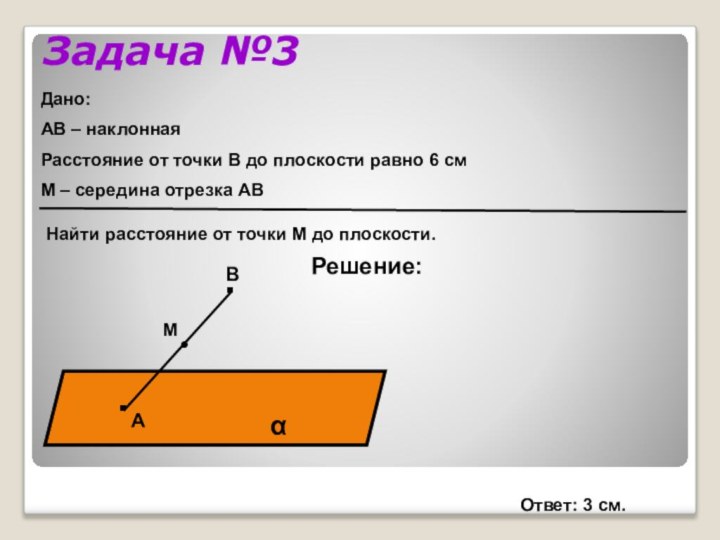
Задача №3
Решение:
Дано:
АВ – наклонная
Расстояние от точки В до
плоскости равно 6 см
М – середина отрезка АВ
Найти расстояние
от точки М до плоскости.Ответ: 3 см.
.
A
B
.
α
•
M
Слайд 11
Задача №4
Решение:
Дано:α, АВ – отрезок не принадлежащий плоскости
Расстояние
от точки А до плоскости равно 5 см
Расстояние от
точки В до плоскости равно 13 смМ – середина отрезка АВ
Найти расстояние от точки М до плоскости.
Ответ: 9 см.
α





























