Презентация на тему шар цилиндр конус

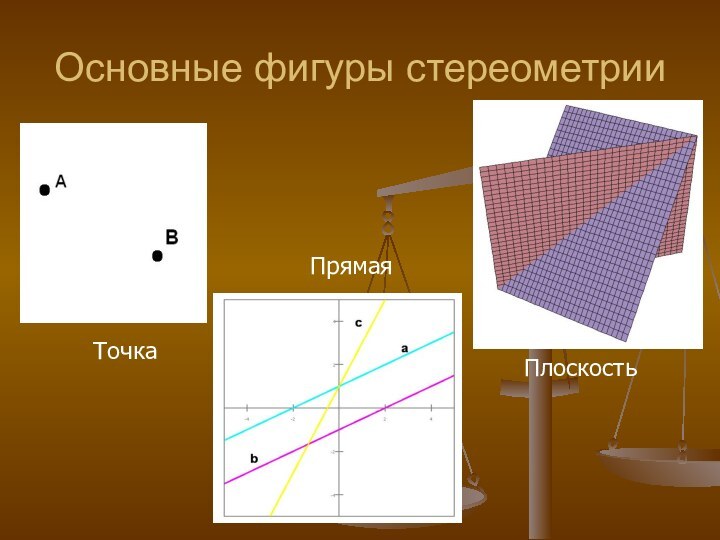
пространственный» и μετρέω — «измеряю») — это раздел геометрии, в котором

изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

Не стоит путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (свойства плоских фигур), а в стереометрии — свойства фигур в пространстве (свойства пространственных фигур).

Плоскость

Многогранник представляет

собой тело, поверхность которого состоит из конечного числа плоских многоугольников. Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми (рис. 1) и невыпуклыми (рис. 2).
Выпуклый многогранник расположен по одну
сторону относительно плоскости,
проходящей через любую его грань .

от данной точки, называемой центром сферы, на одно и

то же расстояние (рис. 11). Отрезок, соединяющий любую точку сферы с ее центром, называется радиусом сферы. Радиусом сферы называют
также расстояние от любой точки
сферы до ее центра. Для сферы,
как и для окружности,
определяются хорды и диаметр.

имеются по крайней мере две точки.
В пространстве существуют

плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.
Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:
любые две точки, принадлежащие разным множествам, разделены плоскостью α;
любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.
Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.