все изученное о неравенствах с одной переменной и способах
их решения;безошибочно воспроизводить любой из выбранных способов решения;
научиться выбирать наиболее рациональный способ решения.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




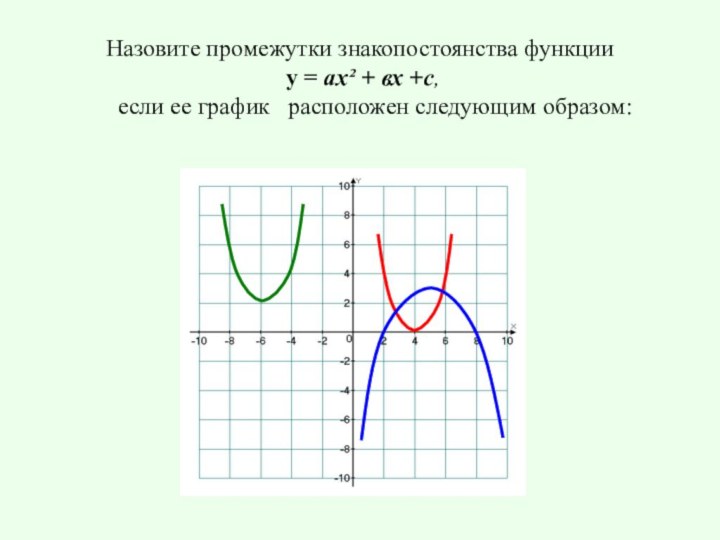









е
а
б
в
г
д
5х2+9х-2<0
1. y=5х2+9х-2
Графиком функции _______ парабола, ветви которой ______ вверх,
т.к. а > 0.
2. у = 0, 5х2+9х-2=0
х1= -2, х2= 0,2
3.
4. y<0 при х Є (-2; 0,2 )
5. х Є (-2; 0,2 )
-2
0
0,2
Пример решения неравенства графическим способом
Вариант-III
Решить неравенство, применяя наиболее рациональный способ решения:
а) -х²+4x-5<0
б)
Вариант-II
a) -x²+8x-12≥0
1. у = -x²+8x-12
2. у=0, -x²+8x-12=0
x²-8x+12=0
Д 1 =16 -12 = 4, Д 1 > 0, 2 корня
х = 4±2
х1= 2, х 2= 6
3.
4. у≥0 при x€[2;6]
Ответ: x€[2;6]
б) (4-x)(x+2)<0
-1(x-4)(x+2)<0
(x-4)(x+2)>0
1. у=(x-4)(x+2)
2. Д(у)=R
3. у=0, (x-4)(x+2)=0
x1= -2, x2= 4
4.
5. у>0 при x€(-∞;-2)U(4;∞)
Ответ: x€(-∞;-2)U(4;∞)
Проверим решение
Вариант-III
a) -x²+4x-5<0
1. у = -x²+4x-5
2. у=0,
-x²+4x-5=0
x²-4x+5=0
Д 1 = 4 – 5 = -1, Д 1 < 0,
корней нет
3.
4. у<0 при x€(-∞;∞)
Ответ: x€(-∞;∞)
б)
(3-x)(x+4)≥0
-1(x-3)(x+4)≥0
(x-3)(x+4)≤0
1. у=(x-3)(x+4)
2. Д(у)=R
3. у=0, x1= - 4, x2= 3
4.
5. у≤0 при x€[-4;3]
Учитывая, что х+4 0, т.е
х -4, получаем х€(-4;3]
Ответ: x€(-4;3]
Домашнее задание.