- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойства функции
Содержание
- 2. План Возрастание и убывание функцииОграниченность функцииНаибольшее и наименьшее значения функцииМаксимум и минимум функцииЧетность и нечетность
- 3. Определение № 1 Функцию у= f(x) называют
- 4. Возрастающая функция Функция возрастает, если большему значению аргумента соответствует большее значение функции.
- 5. Определение № 2 Функцию у= f(x) называют
- 6. Убывающая функция Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
- 7. Обычно термины «возрастающая функция», «убывающая функция» объединяют
- 8. Определение № 3 Функцию у= f(x) называют
- 9. Определение № 4 Функцию у= f(x)
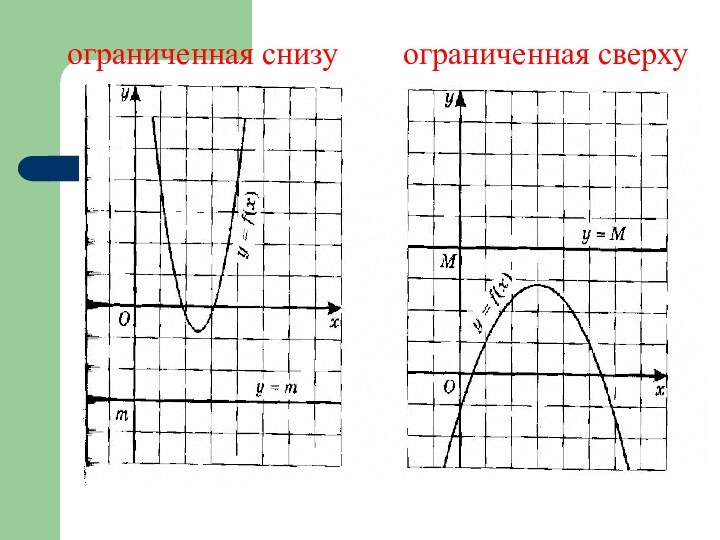
- 10. ограниченная сверхуограниченная снизу
- 11. Если функция ограничена и снизу и
- 12. Определение № 5 Число m называют наименьшим
- 13. Определение № 6 Число М называют набольшим
- 14. Утверждения:Если у функции существует yнаиб, то
- 15. Определение № 7 Точку x0 называют точкой
- 16. Определение № 8Точку x0 называют точкой минимума
- 17. а) Укажите точки экстремума и определите их вид;б) укажите наибольшее и наименьшее значение функции.
- 18. Выпуклость функцииФункция выпукла вниз на промежутке Х,
- 20. Непрерывность функции Непрерывность функции на отрезке
- 22. Определение 11Функцию у= f(x) называют четной, если
- 23. Определение 12Функцию у= f(x) называют нечетной, если
- 25. Утверждения:Если график функции симметричен относительно оси ординат,
- 26. Алгоритм исследования функции 1. Область определения функции2.
- 27. Скачать презентацию
- 28. Похожие презентации
План Возрастание и убывание функцииОграниченность функцииНаибольшее и наименьшее значения функцииМаксимум и минимум функцииЧетность и нечетность












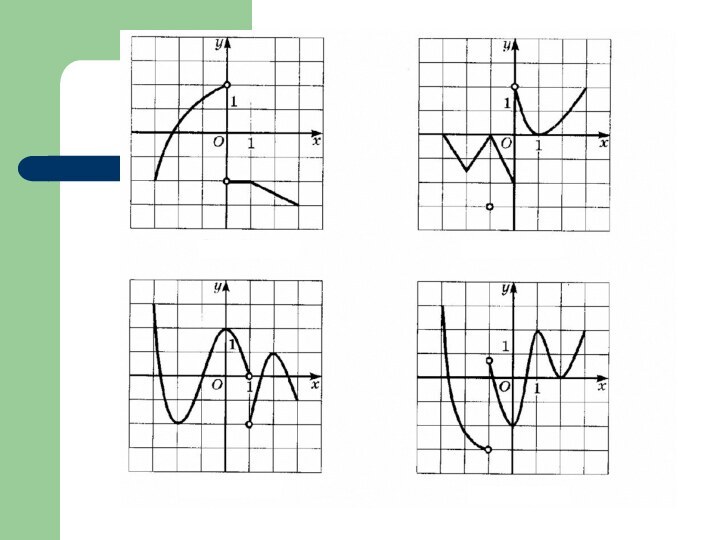





Слайд 2
План
Возрастание и убывание функции
Ограниченность функции
Наибольшее и наименьшее
значения функции
Слайд 3
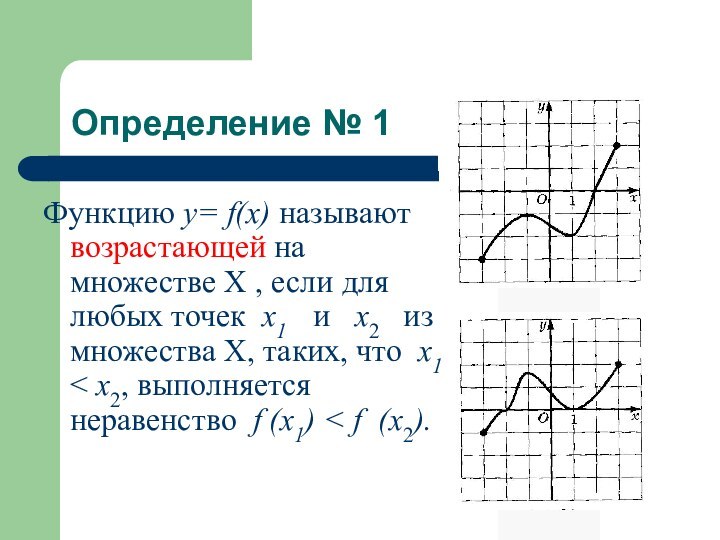
Определение № 1
Функцию у= f(x) называют возрастающей
на множестве Х , если для любых точек x1
и x2 из множества Х, таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).
Слайд 4
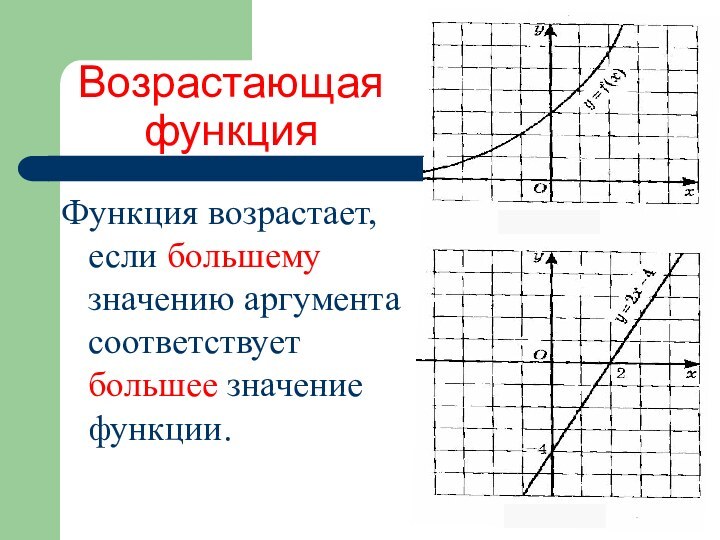
Возрастающая функция
Функция возрастает, если большему значению аргумента
соответствует большее значение функции.
Слайд 5
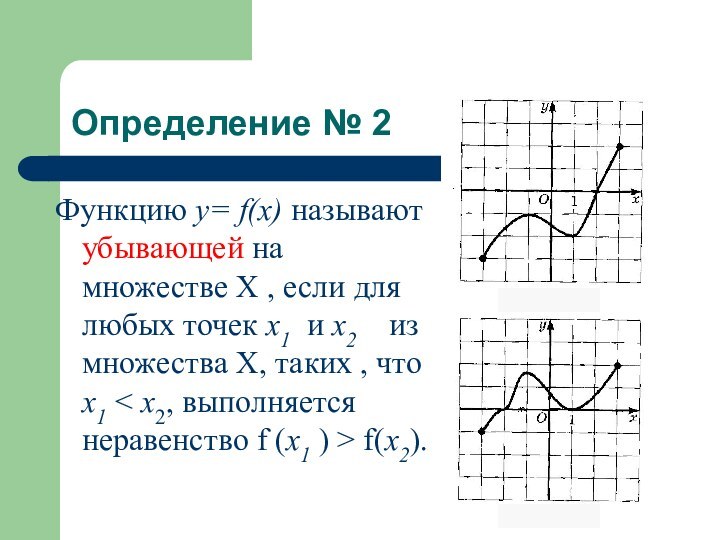
Определение № 2
Функцию у= f(x) называют убывающей
на множестве Х , если для любых точек x1
и x2 из множества Х, таких , что x1 < x2, выполняется неравенство f (x1 ) > f(x2).
Слайд 6
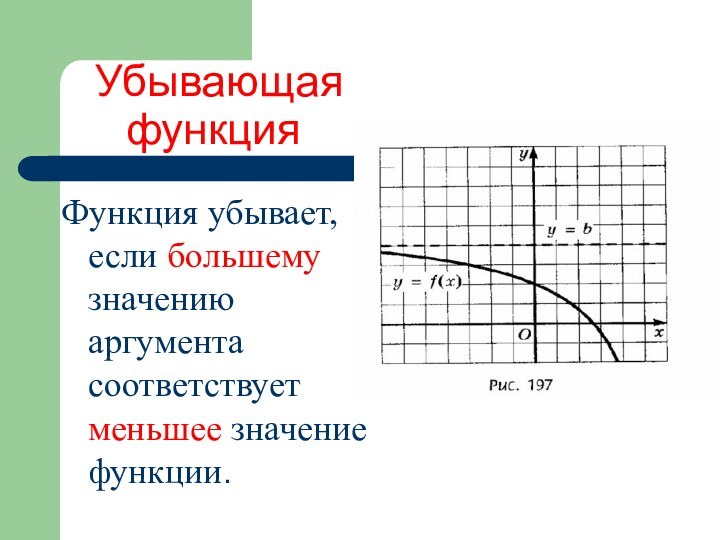
Убывающая
функция
Функция убывает, если большему значению
аргумента соответствует меньшее значение функции.
Слайд 7 Обычно термины «возрастающая функция», «убывающая функция» объединяют общим
названием монотонная функция, а исследование функции на возрастание или
убывание называют исследованием функции на монотонность.
Слайд 8
Определение № 3
Функцию у= f(x) называют ограниченной
снизу на множестве Х, если все значения этой функции
на множестве Х больше некоторого числа, т.е., если существует такое число m, что для любого значения х выполняется неравенство f(x) > m
Слайд 9
Определение № 4
Функцию у= f(x) называют
ограниченной сверху на множестве Х , если все значения
этой функции на множестве Х меньше некоторого числа , т.е. , если существует такое число М , что для любого значения х выполняется неравенство f(x) < М
Слайд 11
Если функция ограничена и снизу и сверху
на всей области определения, то ее называют ограниченной
Слайд 12
Определение № 5
Число m называют наименьшим значением
функции у= f(x) на множестве Х , если:
1)во множестве
Х существует такая точка x0 , что f(x0) = m2) для любого значения х из множества Х выполняется неравенство
Слайд 13
Определение № 6
Число М называют набольшим значением
функции у= f(x) на множестве Х, если:
1)во множестве Х
существует такая точка, что f(x0) = М2) для любого значения х из множества Х выполняется неравенство
Слайд 14
Утверждения:
Если у функции существует yнаиб,
то она
ограничена сверху
Если у функции существует yнаим, то
она ограничена снизу.
Слайд 15
Определение № 7
Точку x0 называют точкой максимума
функции у= f(x), если у этой точки существует окрестность,
для всех точек которой (кроме самой точки x0) выполняется неравенство
Слайд 16
Определение № 8
Точку x0 называют точкой минимума функции
у= f(x), если у этой точки существует окрестность, для
всех точек которой ( кроме самой точки x0) выполняется неравенствоТочки максимума и минимума объединяют общим названием – точки экстремума
Слайд 17
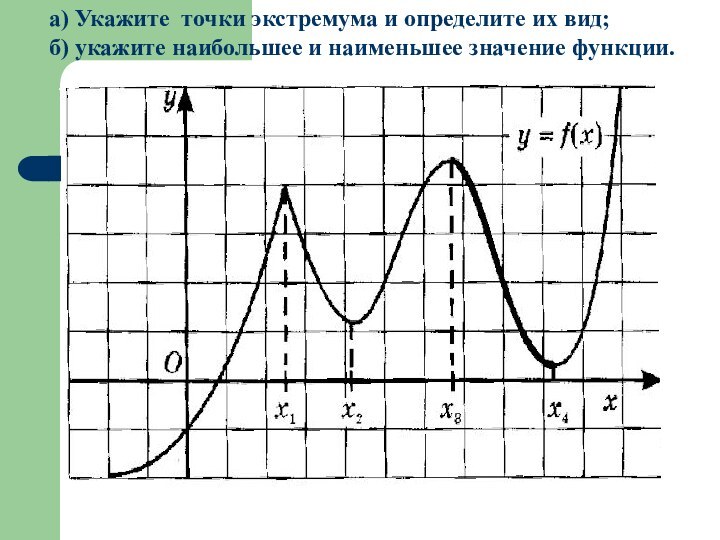
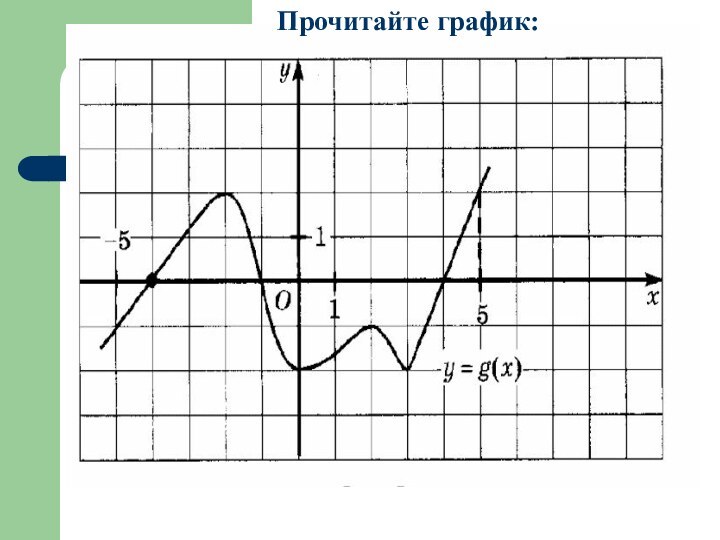
а) Укажите точки экстремума и определите их вид;
б)
укажите наибольшее и наименьшее значение функции.
Слайд 18
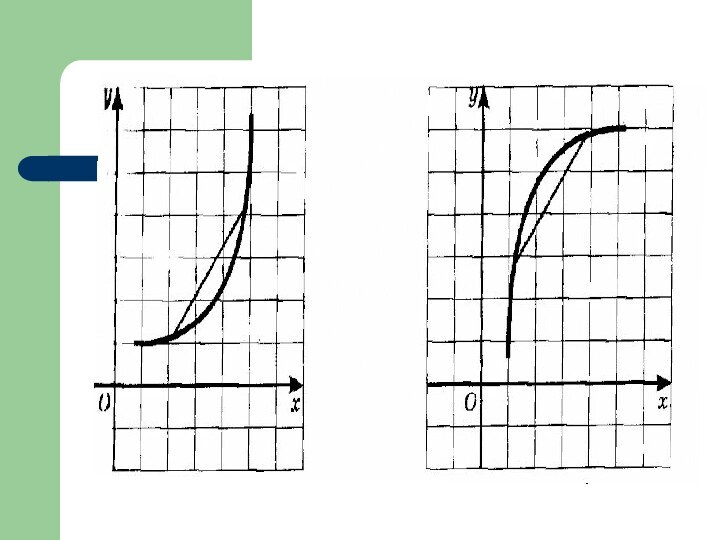
Выпуклость функции
Функция выпукла вниз на промежутке Х, если,
соединив любые две точки ее графика (с абсциссами из
Х) отрезком, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.Функция выпукла вверх на промежутке Х, если, соединив любые две точки ее графика (с абсциссами из Х) отрезком, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.
Определение № 9,10
Слайд 20
Непрерывность
функции
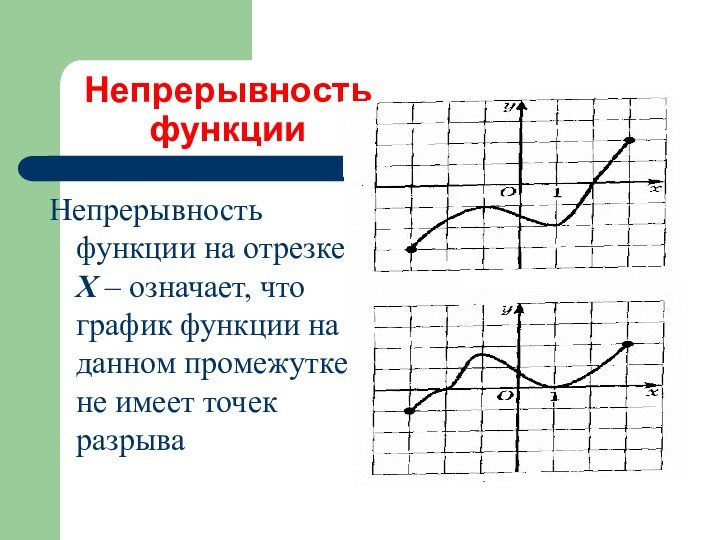
Непрерывность функции на отрезке Х –
означает, что график функции на данном промежутке не имеет
точек разрыва
Слайд 22
Определение 11
Функцию у= f(x) называют четной, если для
любого значения х из множества Х выполняется равенство
Слайд 23
Определение 12
Функцию у= f(x) называют нечетной, если для
любого значения х из множества Х выполняется равенство
Слайд 25
Утверждения:
Если график функции симметричен относительно оси ординат, то
функция четная
Если график функции симметричен относительно начала координат, то
функция нечетная
Слайд 26
Алгоритм исследования функции
1. Область определения функции
2. Четность
, нечетность
3. Непрерывность
4. Выпуклость
5. Нули функции
6. Промежутки возрастания
и убывания 7. Точки экстремума
8. Ограниченность функции
9. Наибольшее и наименьшее значения функции
10. Множество значений функции





























