- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему призмы
Содержание
- 2. Призмой называется многогранник, у которого две грани
- 3. Свойства призмыОснования призмы являются равными многоугольниками;Боковые грани
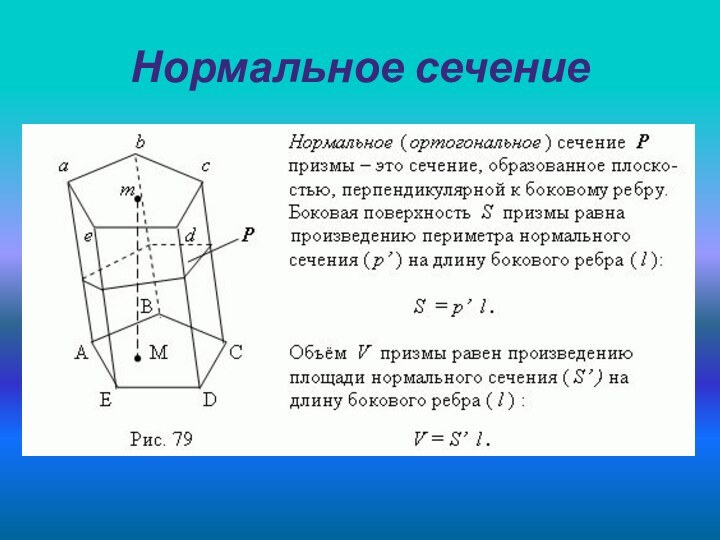
- 4. Нормальное сечение
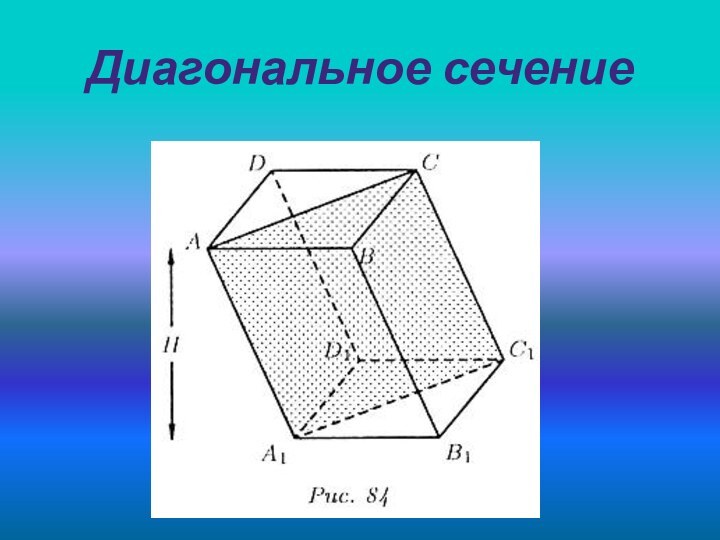
- 5. Диагональное сечение
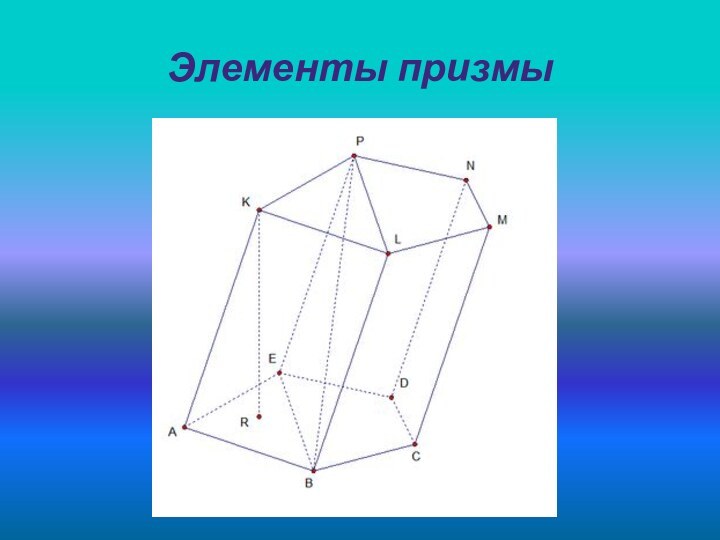
- 6. Элементы призмы
- 7. Виды призмПрямая призма – призма, у которой
- 8. В зависимости от формы основания призмы делят
- 9. Скачать презентацию
- 10. Похожие презентации
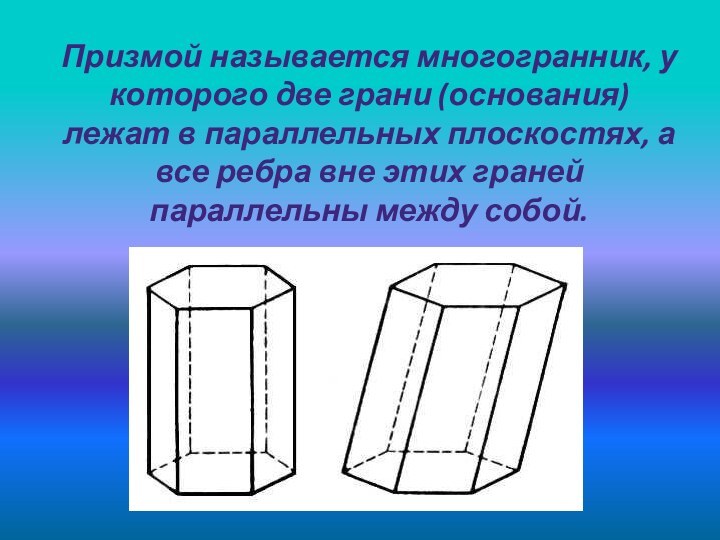
Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.





Слайд 3
Свойства призмы
Основания призмы являются равными многоугольниками;
Боковые грани призмы
являются параллелограммами;
Боковые рёбра призмы параллельны и равны;
Объём призмы равен
произведению её высоты на площадь основания:V=h*S;
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания;
Площадь боковой поверхности произвольной призмы S=P*l;
Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы;
Перпендикулярное сечение перпендикулярно ко всем боковым граням;
Углы - это линейные углы двухгранных углов при соответствующих рёбрах.
Слайд 7
Виды призм
Прямая призма – призма, у которой все
рёбра перпендикулярны основанию, в противном случае она называется наклонной.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра;
В прямой призме боковые рёбра являются высотами;
Площадь боковой поверхности наклонной призмы равна произведению; периметра перпендикулярного сечения на длину бокового ребра;
Объём наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
Слайд 8 В зависимости от формы основания призмы делят на
треугольные, четырёхугольные, пятиугольные и т.д.
Правильная призма – призма, в
основании которой лежит правильный многоугольник, а боковые рёбра перпендикулярны основаниям.Основания правильной призмы являются правильными многоугольниками;
Боковые грани правильной призмы являются правильными прямоугольниками;
Боковые рёбра правильной призмы равны;
Правильная призма является прямой.





























