- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тела вращения
Содержание
- 2. Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
- 3. цилиндр, полученный вращением прямоугольника ABCD вокруг стороны
- 4. Цилиндром называется тело, которое состоит из двух кругов и цилиндрической поверхности
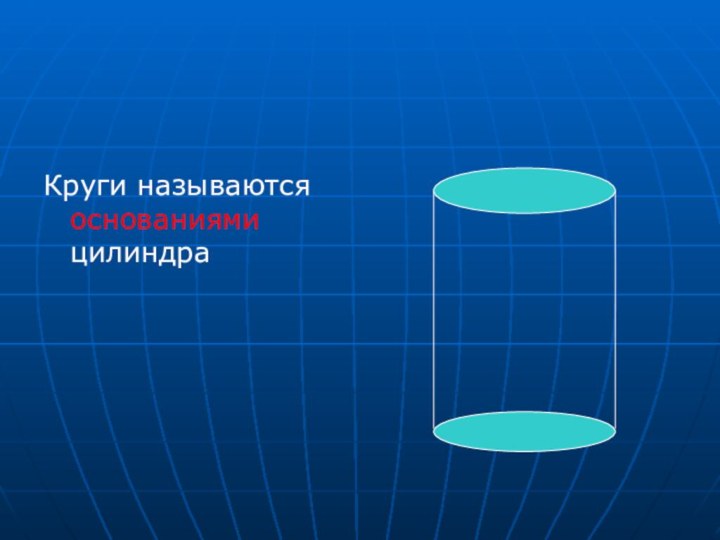
- 5. Круги называются основаниями цилиндра
- 6. Радиусом цилиндра называется радиус его основания.
- 7. Отрезки, из которых состоит цилиндрическая поверхность называются образующими цилиндра
- 8. Высотой цилиндра называется длина образующей
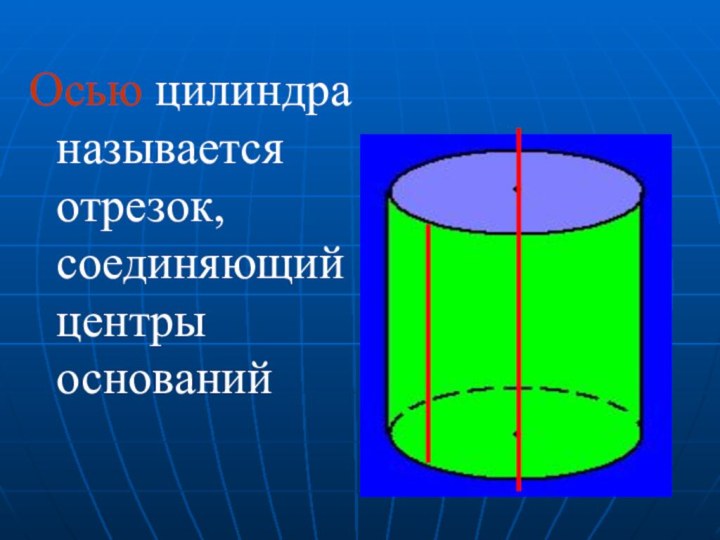
- 9. Осью цилиндра называется отрезок, соединяющий центры оснований
- 10. Если секущая плоскость проходит через ось цилиндра,
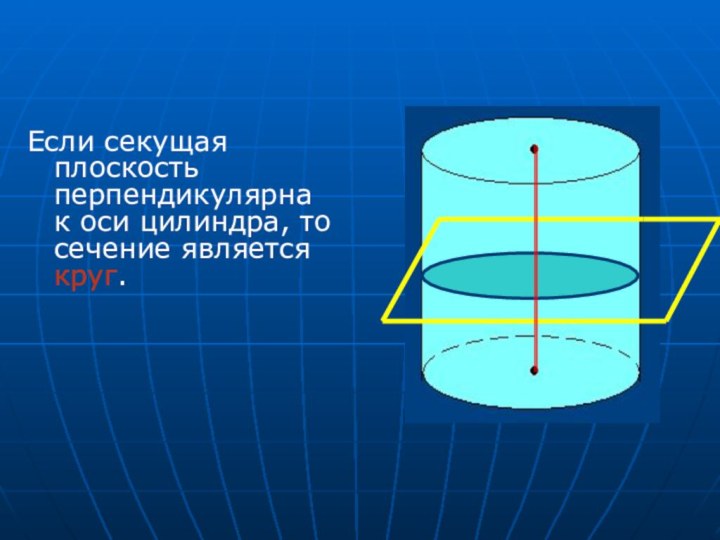
- 11. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является круг.
- 12. Поверхность цилиндра состоит из оснований и боковой поверхности.
- 13. За площадь боковой поверхности цилиндра принимается площадь ее развертки.Sбок=2Пrh
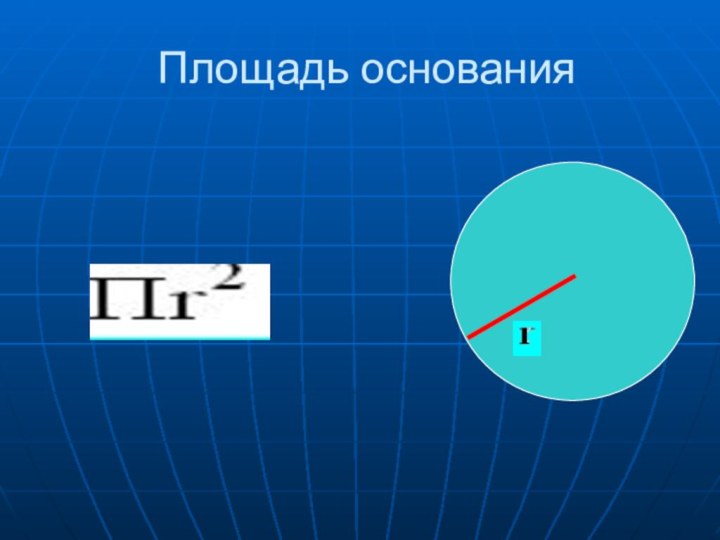
- 14. Площадь основания
- 15. Площадь полной поверхности цилиндра вычисляется по формуле :
- 16. Объем цилиндраVц = π r² h
- 17. конус
- 18. Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.
- 19. На рисунке изображен конус, полученный вращением прямоугольного
- 20. Конус Конусом называется тело, которое состоит из круга – основания конуса и конической поверхности
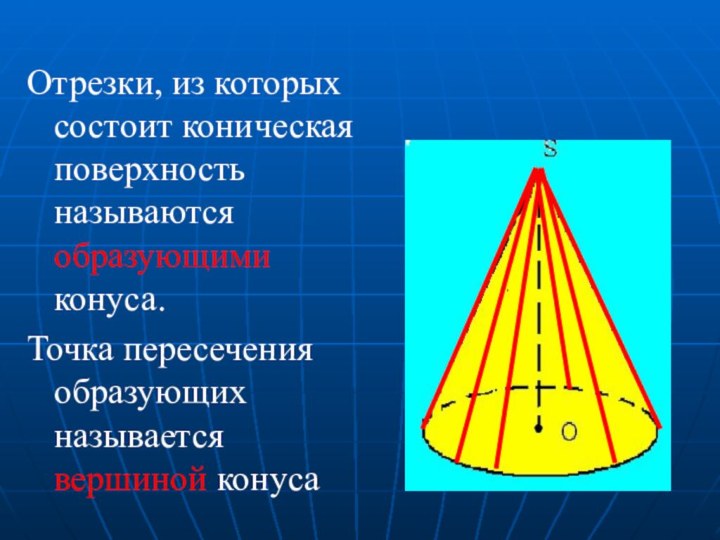
- 21. Отрезки, из которых состоит коническая поверхность называются образующими конуса.Точка пересечения образующих называется вершиной конуса
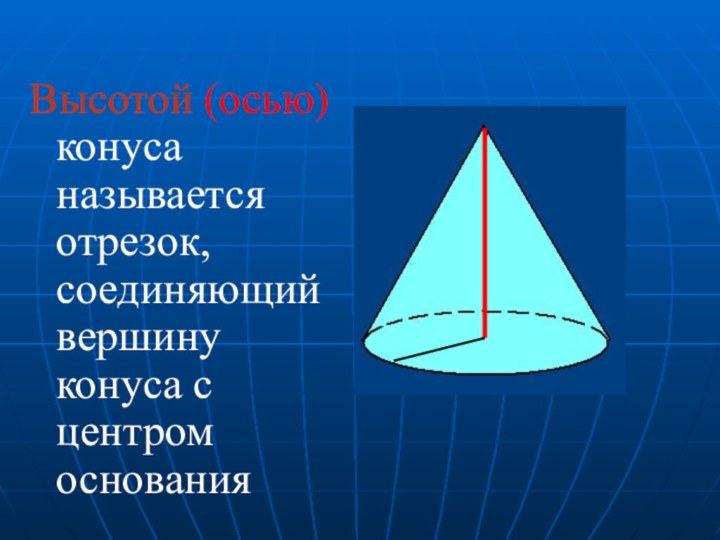
- 22. Высотой (осью) конуса называется отрезок, соединяющий вершину конуса с центром основания
- 23. Сечения конуса плоскостямиЕсли секущая плоскость проходит через
- 24. Если секущая плоскость перпендикулярна к оси конуса,
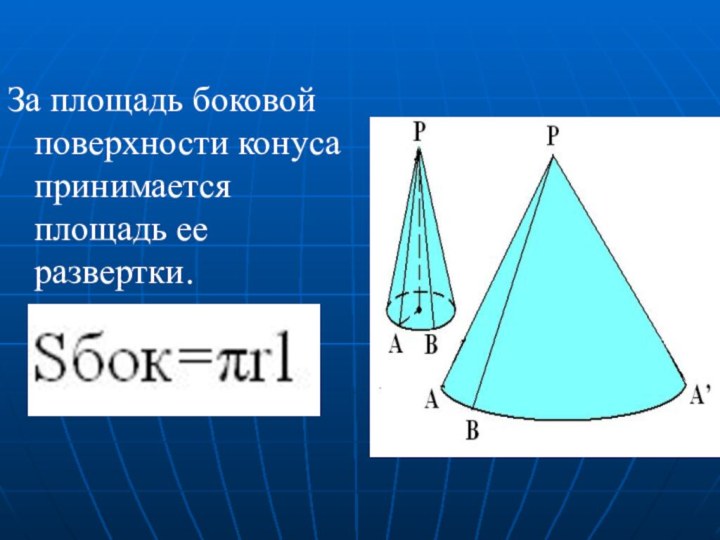
- 25. Площадь полной поверхности конуса Площадь боковой
- 26. За площадь боковой поверхности конуса принимается площадь ее развертки.
- 27. Площадь полной поверхности Площадь полной
- 28. Объем конуса
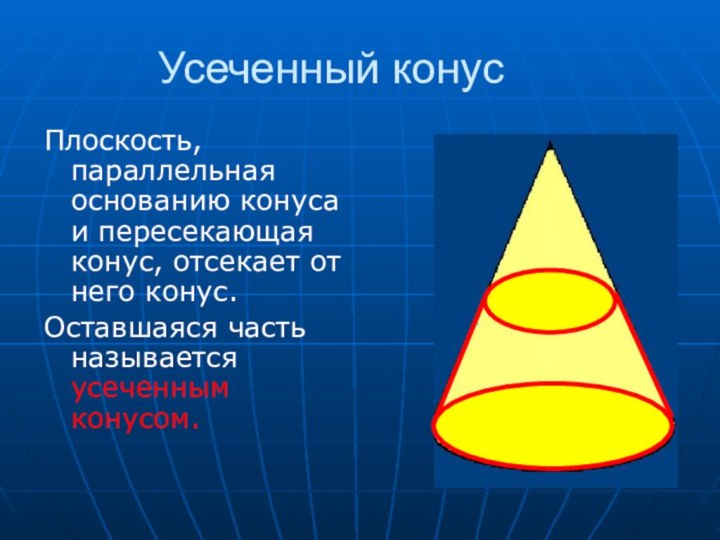
- 29. Усеченный конусПлоскость, параллельная основанию конуса и пересекающая конус, отсекает от него конус.Оставшаяся часть называется усеченным конусом.
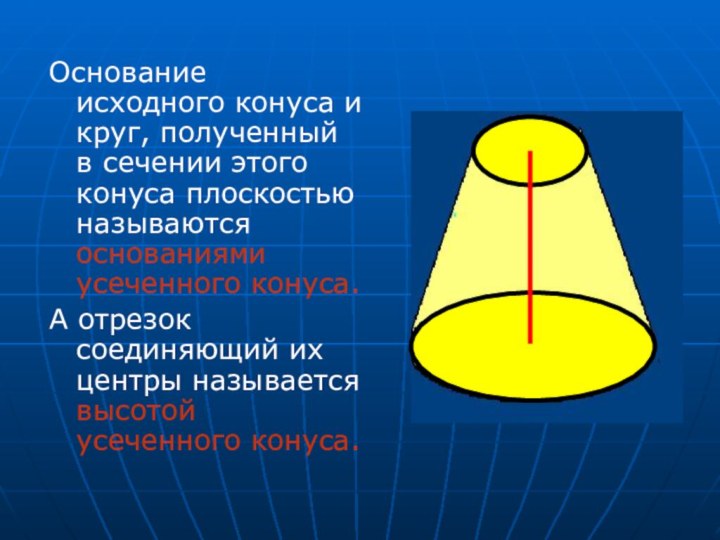
- 30. Основание исходного конуса и круг, полученный в
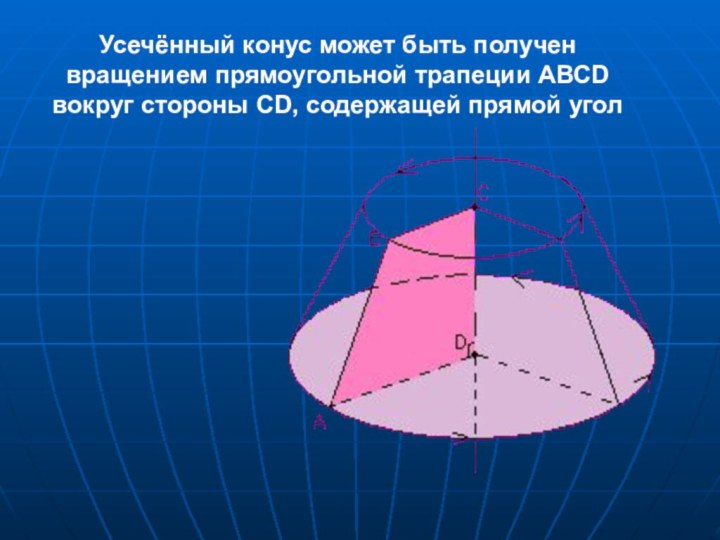
- 31. Усечённый конус может быть получен вращением прямоугольной трапеции АВСD вокруг стороны CD, содержащей прямой угол
- 32. Площадь поверхности усеченного конуса
- 33. Площадь боковой поверхности усеченного конуса вычисляется по
- 34. Объем усеченного конуса
- 35. Сфера
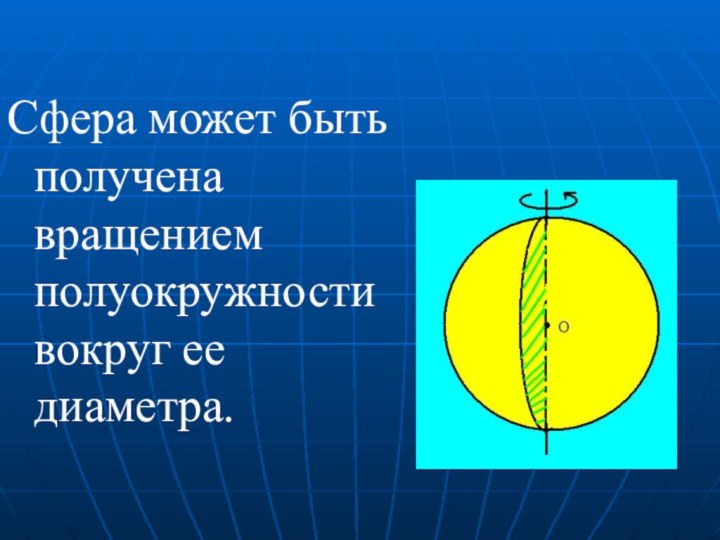
- 36. Сфера может быть получена вращением полуокружности вокруг ее диаметра.
- 37. Сферой называется поверхность, которая состоит из всех
- 38. Любой отрезок, соединяющий центр сферы с точкой
- 39. Площадь сферы вычисляется по формуле
- 40. Шар
- 41. Тело, ограниченное сферой называется шаром
- 42. Шар может быть получен вращением полукруга вокруг его диаметра .
- 43. Объем шара
- 45. Первый спутник Земли
- 46. Планета Марс
- 47. Венера
- 48. Шкатулка - шар
- 49. ФонтаныФОНТАНЫ - ШАРЫ
- 50. дома-сферы
- 51. Сфера − наилучшая форма для дома при
- 52. Обратите внимание:человек в наше время подсознательно начинает
- 53. Скачать презентацию
- 54. Похожие презентации
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.



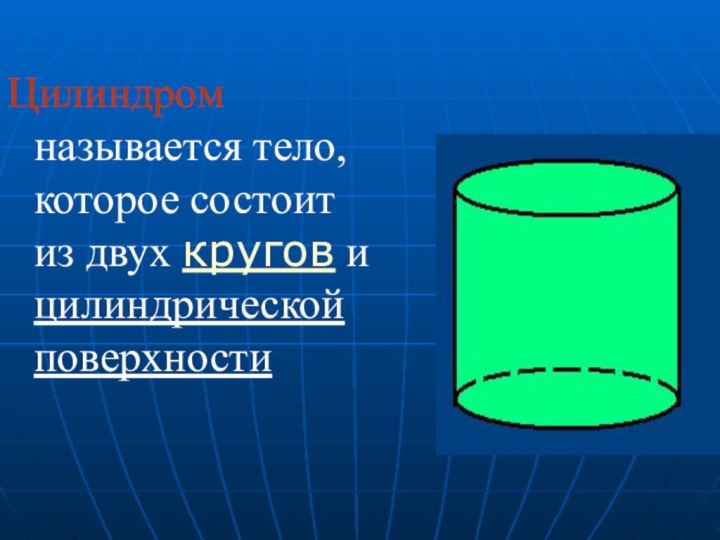

































Слайд 3 цилиндр, полученный вращением прямоугольника ABCD вокруг стороны AB.
При этом боковая поверхность цилиндра образуется вращением стороны CD,
а основание - вращением сторон BC и AD.Слайд 10 Если секущая плоскость проходит через ось цилиндра, то
сечение представляет собой прямоугольник, две стороны которого –образующие, а
две другие - диаметры оснований цилиндра. Такое сечение называется осевымСечения цилиндра плоскостями
Слайд 18 Конус может быть получен вращением прямоугольного треугольника вокруг
одного из его катетов.
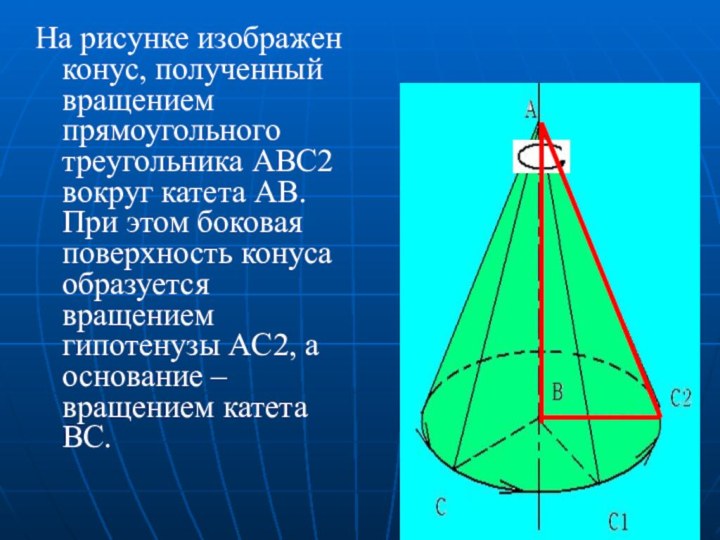
Слайд 19 На рисунке изображен конус, полученный вращением прямоугольного треугольника
ABC2 вокруг катета AB. При этом боковая поверхность конуса
образуется вращением гипотенузы AC2, а основание – вращением катета BC.
Слайд 20
Конус
Конусом называется тело, которое состоит из круга
– основания конуса и конической поверхности
Слайд 21 Отрезки, из которых состоит коническая поверхность называются образующими
конуса.
Точка пересечения образующих называется вершиной конуса
Слайд 23
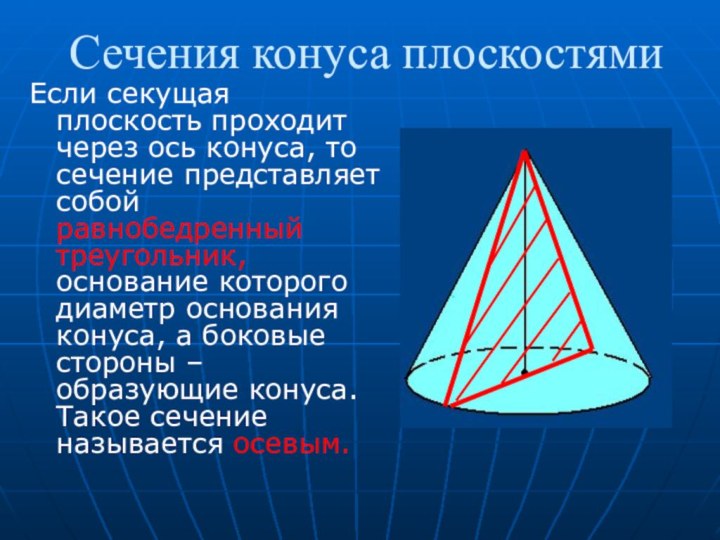
Сечения конуса плоскостями
Если секущая плоскость проходит через ось
конуса, то сечение представляет собой равнобедренный треугольник, основание которого
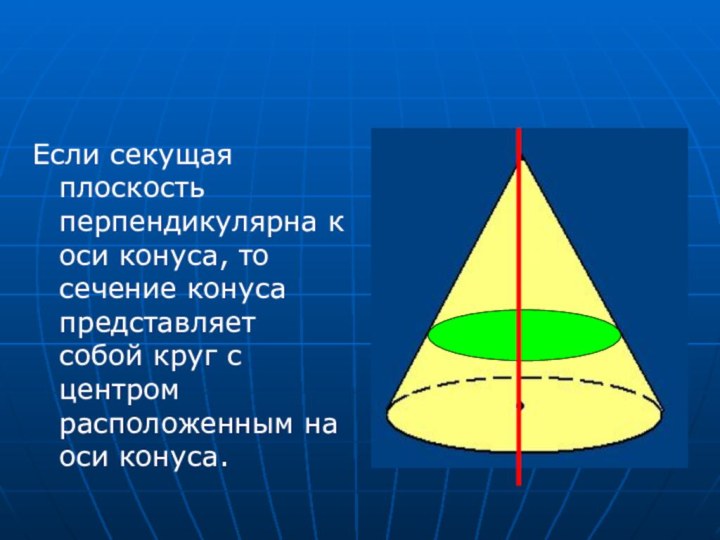
диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым.Слайд 24 Если секущая плоскость перпендикулярна к оси конуса, то
сечение конуса представляет собой круг с центром расположенным на
оси конуса.
Слайд 27
Площадь полной поверхности
Площадь полной поверхности конуса
вычисляется по формуле:
где L – длина образующей, r –
радиус окружности.
Слайд 29
Усеченный конус
Плоскость, параллельная основанию конуса и пересекающая конус,
отсекает от него конус.
Оставшаяся часть называется усеченным конусом.
Слайд 30 Основание исходного конуса и круг, полученный в сечении
этого конуса плоскостью называются основаниями усеченного конуса.
А отрезок соединяющий
их центры называется высотой усеченного конуса.
Слайд 31 Усечённый конус может быть получен вращением прямоугольной трапеции
АВСD вокруг стороны CD, содержащей прямой угол
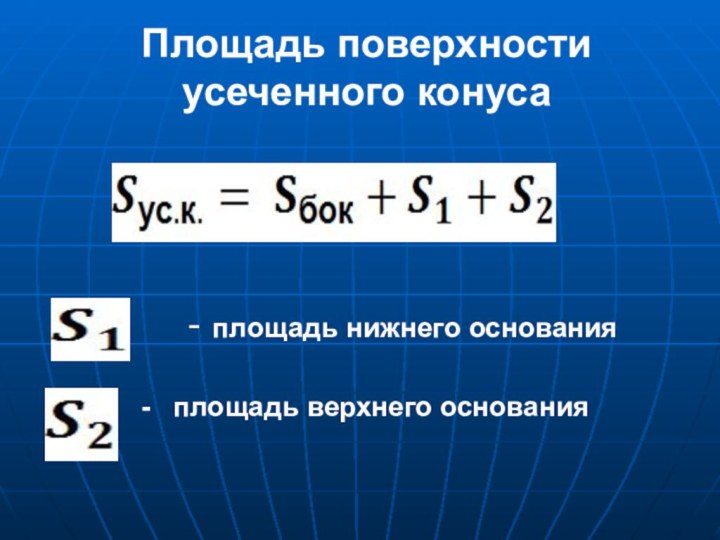
Слайд 32
Площадь поверхности усеченного конуса
- площадь нижнего основания
- площадь верхнего основания
Слайд 33 Площадь боковой поверхности усеченного конуса вычисляется по формуле:
- радиус верхнего основания
- образующая
Слайд 37 Сферой называется поверхность, которая состоит из всех точек
пространства, находящихся на данном расстоянии от данной точки. Эта
точка называется центром сферы.
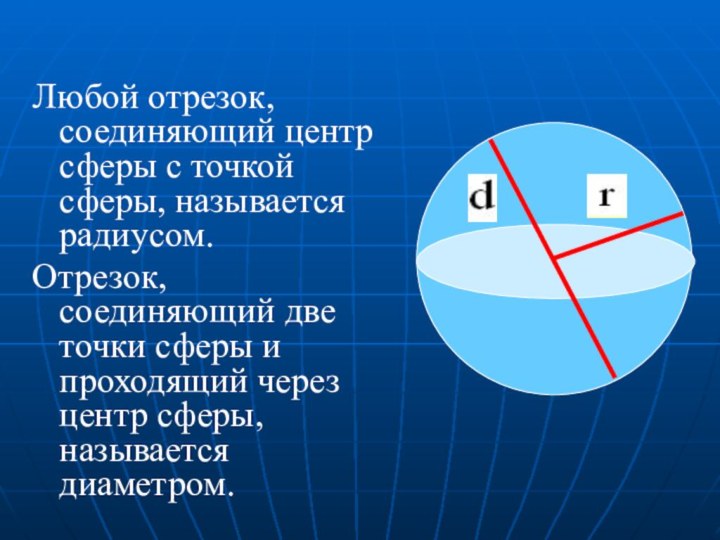
Слайд 38 Любой отрезок, соединяющий центр сферы с точкой сферы,
называется радиусом.
Отрезок, соединяющий две точки сферы и проходящий через
центр сферы, называется диаметром.
Слайд 51 Сфера − наилучшая форма для дома при ветровых
и снеговых нагрузках.
Сфера имеет наибольший объём при наименьшей
площади поверхности. Минимальны материалоёмкость, трудоёмкость и время создания сферы.
Так как сфера изготавливается бесшовной, минимизируются теплопотери; отопительная система минимальная.
Не нужен ремонт кровли-крыши, ибо она не течёт.
Дом-сфера дёшев в эксплуатации; нет необходимости ремонтировать фасады, перекрытия, чердаки, красить фасады и крыши.
Ввиду лёгкости и прочности сфер целесообразно их строительство в сейсмически опасных районах.
Поверхность шара примерно на четверть меньше, чем поверхность куба такого же объёма. Это означает, что на шарообразные сооружения нужно расходовать материалов на четверть меньше, чем на кубические. В сферических сооружениях нет углов, где обычно застаивается воздух, их легче проветривать.