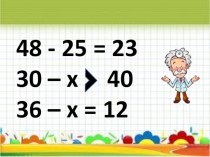- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Формализм задачи линейной оптимизации на примере транспортной задачи
Содержание
- 2. Вопрос . Постановка транспортной задачи . Решение средствами MS Excel.
- 3. Вопрос 1. Постановка транспортной задачи . Решение средствами MS Excel.
- 4. Считаем, что некоторая однородная продукция находится у
- 6. Рассмотрим постановку и математическую модель одной из
- 7. Потребность в данном товаре каждого j-го потребителя
- 8. Закрытая задача (модель): суммарные запасы поставщиков равняются
- 9. Математическая модель транспортной задачи
- 10. Пусть на складах А1, А2, АЗ, А4,
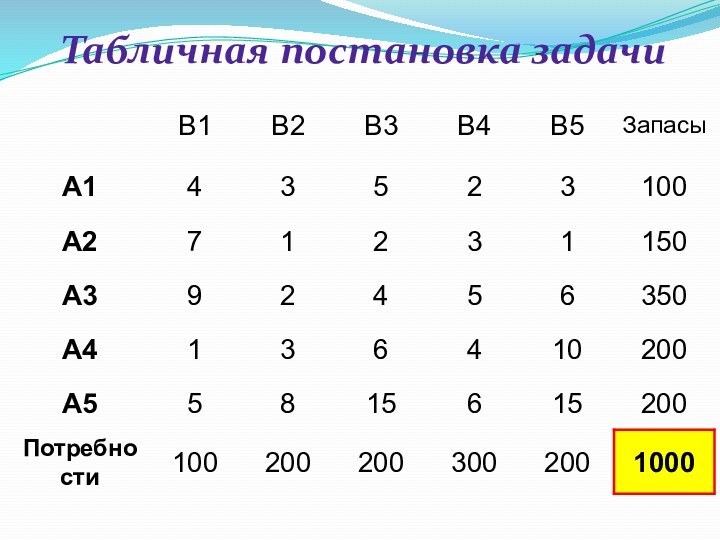
- 12. Табличная постановка задачи
- 13. Математическая модельВведение переменныхX11- кол-во груза которое нужно
- 14. Математическая модельВведение переменныхX21- кол-во груза которое нужно
- 15. Математическая модельВведение переменныхОбщая записьXij- кол-во груза которое
- 16. Математическая модель2. Определение целевой функцииF=4x11+3x12+5x13+2x14+3x15+7x21+x22+2x23+3x24+x25+9x31+2x32+4x33+5x34+6x35+x41+3x42+6x43+4x44+10x45+5x51++8x52+15x53+6x54+15x55
- 17. Математическая модель2. Ограниченияx11+x12+x13+x14+x15=100x21+x22+x23+x24+x25=150x31+x32+x33+x34+x35=350x41+x42+x43+x44+x45=200x51+x52+x53+x54+x55=200
- 18. Математическая модель2. Ограниченияx11+x21+x31+x41+x51=100x12+x22+x32+x42+x52=200x13+x23+x33+x43+x53=200x14+x24+x34+x44+x54=300x15+x25+x35+x45+x55=200Xij>=0демонстрация
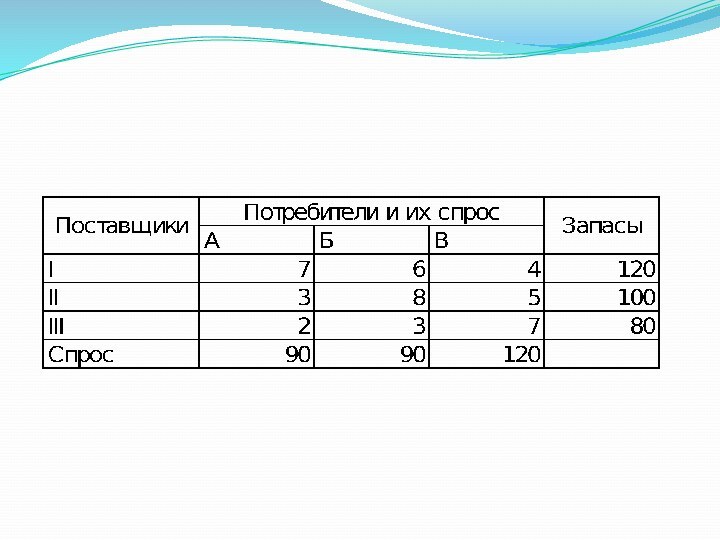
- 19. Транспортная задача 2Три поставщика одного и того
- 21. Скачать презентацию
- 22. Похожие презентации
Вопрос . Постановка транспортной задачи . Решение средствами MS Excel.
















Слайд 4 Считаем, что некоторая однородная продукция находится у нескольких
поставщиков в различных объёмах.
Необходимо доставить эту продукцию ряду потребителей
в разных количествах.Известны стоимости перевозки единицы продукции от каждого поставщика каждому потребителю.
Требуется составить такой план перевозок, при котором суммарные затраты на перевозку всех грузов минимальны.
Слайд 6 Рассмотрим постановку и математическую модель одной из задач
линейной оптимизации, которая получила название транспортной задачи.
Необходимо доставить от
поставщиковi ( ) некоторый однородный груз (товар) в объеме ai единиц потребителям с минимальными транспортными издержками (здесь m и n – конечные числа).
Слайд 7 Потребность в данном товаре каждого j-го потребителя известна
и составляет bj единиц.
Известны также cij – величины
стоимости перевозки единицы груза от i-го поставщика к j-му потребителю. Следует составить такой план перевозок xij , при котором суммарная стоимость перевозки груза (товара) будет минимальной, т.е.
Слайд 8 Закрытая задача (модель): суммарные запасы поставщиков равняются суммарным
запросам потребителей.
Открытая модель (задача с нарушенным балансом): запасы поставщиков
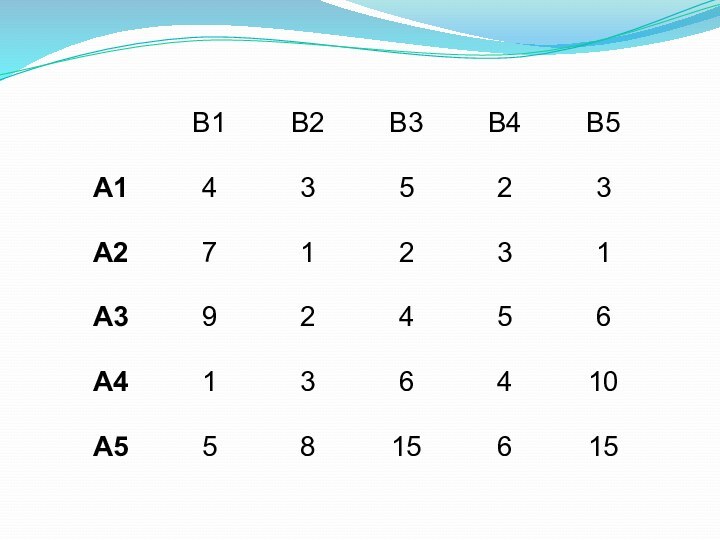
не равны запросам потребителей.Слайд 10 Пусть на складах А1, А2, АЗ, А4, А5
хранится однотипная продукция в количестве соответственно 100, 150, 350,
200, 200 единиц.Эту продукцию необходимо доставить потребителям В1, В2, В3, В4, В5 по их заказам: 100, 200, 200, 300, 200 единиц соответственно.
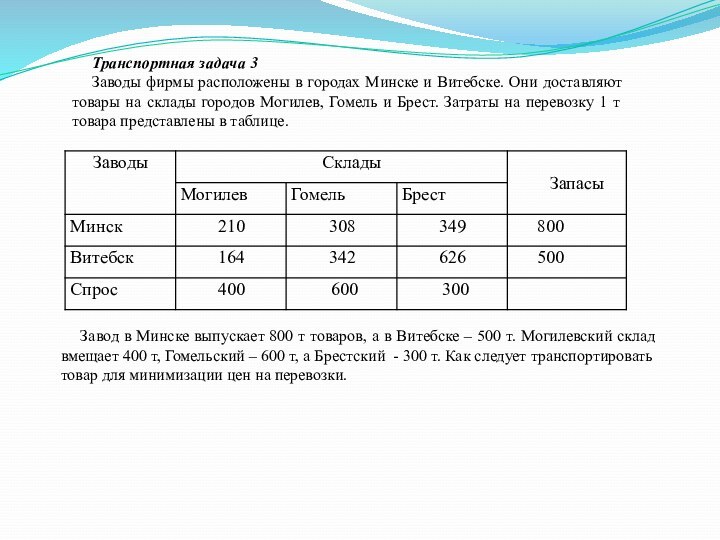
Стоимость перевозки одной единицы груза из каждого пункта отправления в каждый пункт назначения задается следующей таблицей:
Закрытая транспортная задача
Слайд 13
Математическая модель
Введение переменных
X11- кол-во груза которое нужно вести
от 1 поставщика 1 потребителю;
X12- кол-во груза которое нужно
вести от 1 поставщика 2 потребителю;X13- кол-во груза которое нужно вести от 1 поставщика 3 потребителю;
X14- кол-во груза которое нужно вести от 1 поставщика 4 потребителю;
X15- кол-во груза которое нужно вести от 1 поставщика 5 потребителю;
Слайд 14
Математическая модель
Введение переменных
X21- кол-во груза которое нужно вести
от 2 поставщика 1 потребителю;
X22- кол-во груза которое нужно
вести от 2 поставщика 2 потребителю;X23- кол-во груза которое нужно вести от 2 поставщика 3 потребителю;
X24- кол-во груза которое нужно вести от 2 поставщика 4 потребителю;
X25- кол-во груза которое нужно вести от 2 поставщика 5 потребителю;
и тд.