Презентация на тему по математике на тему Графики простейших функций. Решение систем уравнений графическим способом

у = 3х-15

3. Графиком

х

У

0

b, где k и b - некоторые

х

у

Графиком линейной функции является прямая.
k – угловой коэффициент прямой
k = t q α

0

α

то линейная функция называется прямой пропорциональностью.
2.Если k = 0,

у

х

у = k х

y = b

у

х

0

0

+ с, где а, в, с – некоторые числа,

а) а > 0

б) а < 0

ветви вверх ветви вниз

0

0

n – натуральное число
1) n – четное,

х

у

х

у

0

0

, где k – число, отличное от 0.

у

Графиком является гипербола

k > 0

k < 0

х

х

у

0

0

= [0;+∞).
y = √¯x
x
y
0

R ; E (y) = [0;+∞) .
x
y
0

График функции y= f (x) + b при

0 1 x

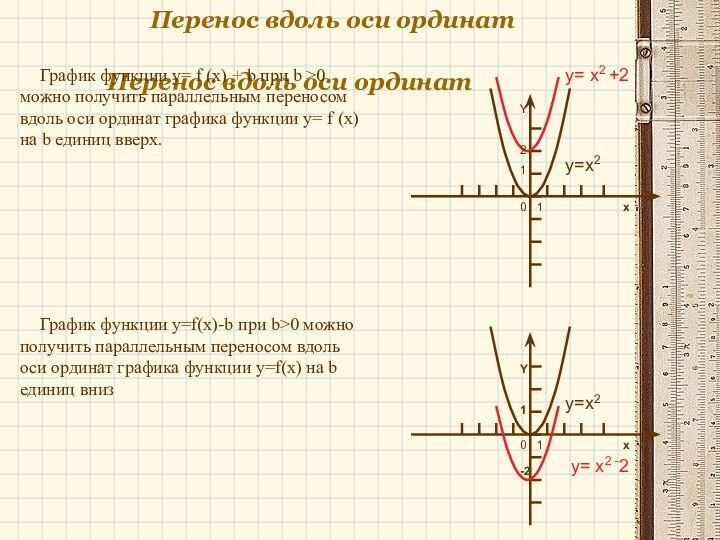
y= x2 +2

y=x2

0 1 x

y= x2 -2

y=x2

Y

2
1

Y

1


-2

y= f (x + c) можно получить параллельным

-2 0 1 x

y=x2

y=(x+2)2

0 1 2 x

y=x2

y=(x-2)2

Y


1

Y


1

( растяжение ) графика вдоль оси ординат
График функции y=

1

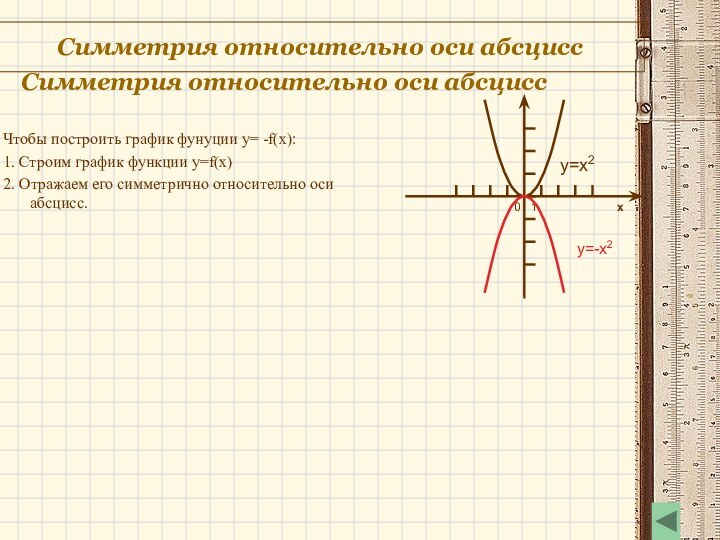
y=x2

y=-x2

Чтобы построить график фунуции y= -f(x):
1. Строим график функции y=f(x)
2. Отражаем его симметрично относительно оси абсцисс.

каких-либо функций?

+ b

+ bx +c

kx
y = kx + m
y = x2
y = 1/x
Прямая,

Парабола

Гипербола

Прямая, проходящая через
начало координат

Прямая

Задание №3. Выберите описание
каждой математической
модели.

является графиком
функции прямой
пропорциональности?

определения и множество значений функции

х
х
у
у
0
0
2
2
D(x)=(-∞;2)∪(2;+∞)
Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)
D(x)=(-∞;0)∪(0;+∞)

точки по оси Ох?
п
а
б
а
л
о
а
б
а
с
ц
с
а
с

точки по оси Оу?
п
а
б
а
л
о
а
б
а
с
ц
с
а
с

р
о
н
и
д
а
т

п
а
б
а
л
о
а
б
а
с
ц
с
а
с

р
о
н
и
д
а
т
р
о
а
л
у
м

координат.


3.
Составим таблицы значений функций.

А
В

координат.


3.
Составим таблицы значений функций.

нет

(0; 0)