Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Интерактивная лекция Множества. Операции над множествами

Содержание

2. основатель теории множеств Георг Кантор«Множество есть многое, мыслимое нами как единое»
3. Основные понятия теории множеств Множество- совокупность объектов,
4. множество людей на Солнцемножество прямых углов равностороннего
5. Примеры числовых множествМНОЖЕСТВО ЧЕТНЫХ ЧИСЕЛ:2, 4, 6,
6. N – множество натуральных чисел;
7. C
8. Множество четырехугольниковПространственные тела1, 2, 3, 4, 5,
9. ВИДЫ МНОЖЕСТВЗапишите множества букв слов КОНИ И КИНОРавные множества{К, О, Н, И}{К, И, Н, О}
10. Даны множества: М = {5, 4, 6},
11. ВИДЫ МНОЖЕСТВА = {2; 3; 5; 7; 11; 13}; {х | 5< х
12. ВИДЫ МНОЖЕСТВ{1; 4; 9; 16; 25; …};
13. Среди перечисленных ниже множеств укажите
14. Основные способы задания множеств1. Перечисление элементов. Элементы
15. ХАРАКТЕРИСТИЧЕСКОЕ СВОЙСТВО МНОЖЕСТВА – СВОЙСТВО, КОТОРЫМ ОБЛАДАЮТ
16. «МНОЖЕСТВО ВСЕХ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 1 ДО
17. В – МНОЖЕСТВО НАТУРАЛЬНЫХ ЧИСЕЛ, КРАТНЫХ 55,
18. C = { y|y=2x, x N,
19. Задайте множество цифр, с помощью
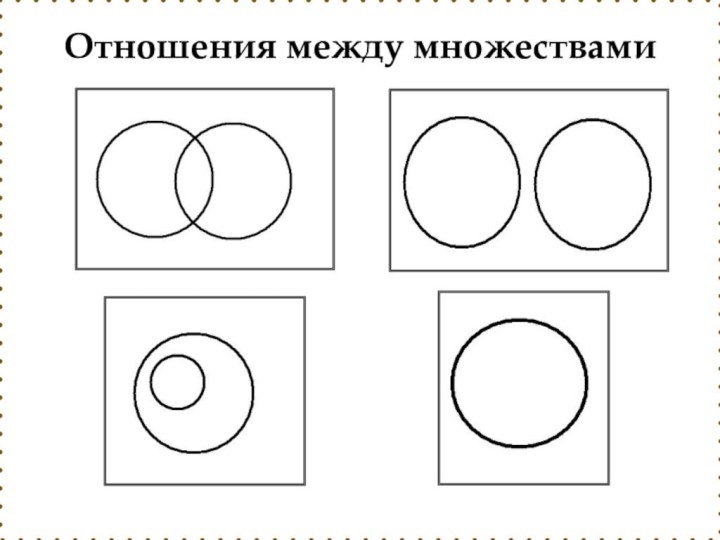
20. Отношения между множествами
21. Множество В, каждый элемент которого принадлежит множеству
22.
23.
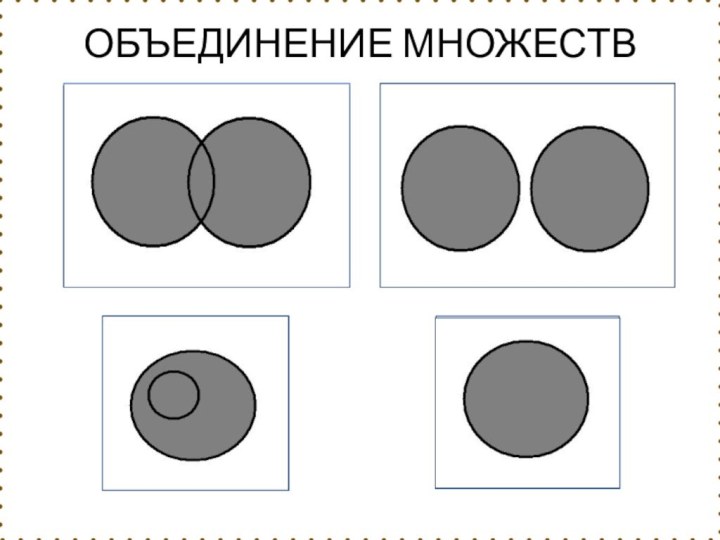
24. Суммой, или объединением множеств А и В
25. ОБЪЕДИНЕНИЕ МНОЖЕСТВ
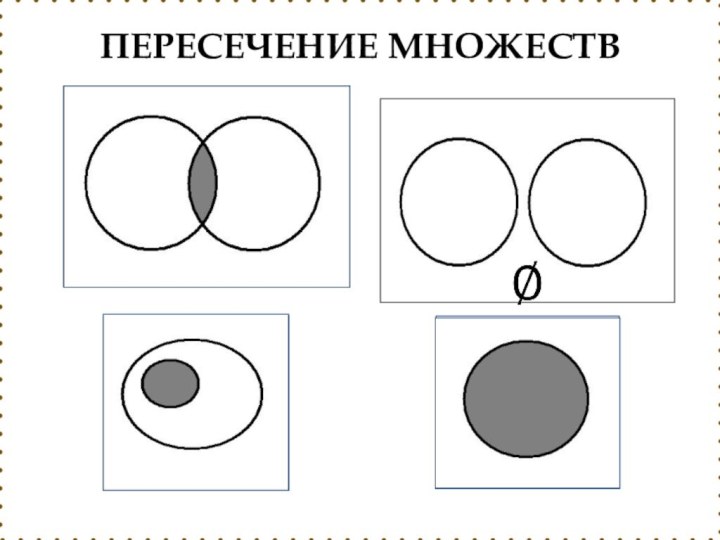
26. Пересечением любого конечного или бесконечного множества множеств
27. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
28. Даны множества: А = {2; 3;
29. Даны множества: А = {a, b,
30. Даны множества: А – множество всех натуральных
31. k Решение задачи с помощью кругов ЭйлераЛеонард
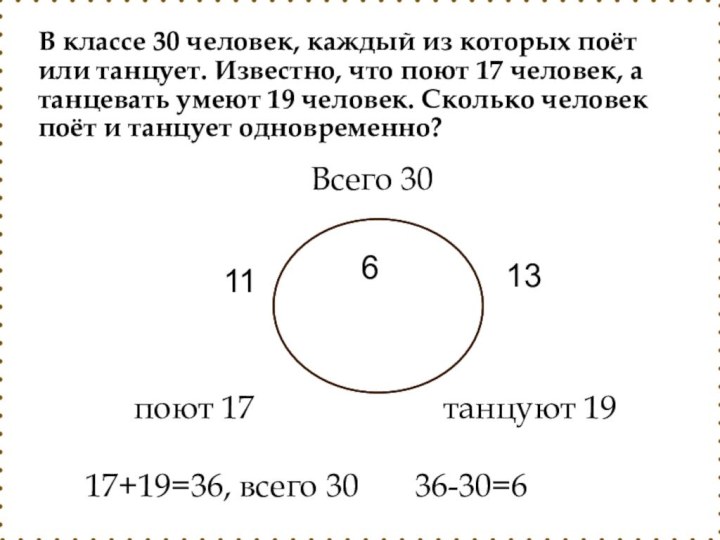
32. поют 17танцуют 19Всего 3017+19=36, всего 3036-30=661113В классе
33. Всего 67Английский 47Немецкий 352347-23=242435-23=121224+12+23=5967- 59=8На фирме работают
34. Каждый учащийся в классе изучает английский или
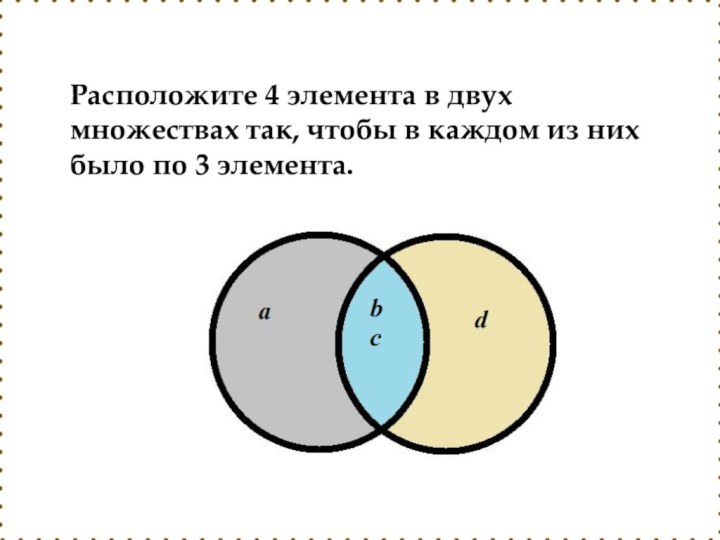
35. Расположите 4 элемента в двух множествах так, чтобы в каждом из них было по 3 элемента.
36. Множества А и В содержат соответственно 5
37. Каждая семья, живущая в нашем доме, выписывает
38. Задачи для самостоятельного решения
39. На школьной спартакиаде каждый из 25 учеников
40. Из 52 школьников 23 собирают значки, 35
41. Скачать презентацию
42. Похожие презентации

основатель теории множеств Георг Кантор«Множество есть многое, мыслимое нами как единое»

Главная
Математика
Интерактивная лекция Множества. Операции над множествами

основатель теории множеств Георг Кантор«Множество есть многое, мыслимое нами как единое»

Основные понятия теории множеств Множество- совокупность объектов, обладающих определенным свойством, объединенных в

множество людей на Солнцемножество прямых углов равностороннего треугольникамножество точек пересечения двух параллельных

Примеры числовых множествМНОЖЕСТВО ЧЕТНЫХ ЧИСЕЛ:2, 4, 6, 8, …МНОЖЕСТВО ДВУЗНАЧНЫХ ЧИСЕЛ:10, 11,

N – множество натуральных чисел; Z – множество целых

Множество четырехугольниковПространственные тела1, 2, 3, 4, 5, 6, 7, 8, 9, 10,

ВИДЫ МНОЖЕСТВЗапишите множества букв слов КОНИ И КИНОРавные множества{К, О, Н, И}{К, И, Н, О}

Даны множества: М = {5, 4, 6}, Р = {4, 5, 6},

ВИДЫ МНОЖЕСТВА = {2; 3; 5; 7; 11; 13}; {х | 5< х

ВИДЫ МНОЖЕСТВ{1; 4; 9; 16; 25; …}; {10; 20; 30; 40; 50;

Среди перечисленных ниже множеств укажите конечные и бесконечные множества:а) множество

Основные способы задания множеств1. Перечисление элементов. Элементы перечисляются в фигурных скобках через

ХАРАКТЕРИСТИЧЕСКОЕ СВОЙСТВО МНОЖЕСТВА – СВОЙСТВО, КОТОРЫМ ОБЛАДАЮТ ВСЕ ЭЛЕМЕНТЫ ЭТОГО МНОЖЕСТВА И

«МНОЖЕСТВО ВСЕХ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 1 ДО 14 ВКЛЮЧИТЕЛЬНО» A={1, 2, 3,

В – МНОЖЕСТВО НАТУРАЛЬНЫХ ЧИСЕЛ, КРАТНЫХ 55, 10, 15, 20, 25, …В

Задайте множество цифр, с помощью которых записывается число: а)

Множество В, каждый элемент которого принадлежит множеству А, называется подмножеством множества А. Например, множество всех

Интерактивная лекция Множества. Операции над множествами

Суммой, или объединением множеств А и В называется множество, состоящее из элементов,

Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из тех

Даны множества: А = {2; 3; 8}, В = {2; 3;

Даны множества: А = {a, b, c, d}, B = {c,

Даны множества: А – множество всех натуральных чисел, кратных 10, В =

k Решение задачи с помощью кругов ЭйлераЛеонард Эйлер — швейцарский, немецкий и

поют 17танцуют 19Всего 3017+19=36, всего 3036-30=661113В классе 30 человек, каждый из которых

Всего 67Английский 47Немецкий 352347-23=242435-23=121224+12+23=5967- 59=8На фирме работают 67 человек. Из них 47

Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают

Расположите 4 элемента в двух множествах так, чтобы в каждом из них было по 3 элемента.

Множества А и В содержат соответственно 5 и 6 элементов, а множество

Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или

На школьной спартакиаде каждый из 25 учеников 9 –го класса выполнил норматив

Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 –

В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в

Слайды презентации

Слайд 2 основатель теории множеств
Георг Кантор
«Множество есть многое, мыслимое

нами как единое»

Слайд 3 Основные понятия теории множеств
Множество- совокупность объектов, обладающих определенным

Основные понятия теории множеств Множество- совокупность объектов, обладающих определенным свойством, объединенных

свойством, объединенных в единое целое.

Объекты, составляющие множество, называются элементами

множества.

Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д.

Приведите примеры множеств

Слайд 4 множество людей на Солнце
множество прямых углов равностороннего треугольника
множество

множество людей на Солнцемножество прямых углов равностороннего треугольникамножество точек пересечения двух

точек пересечения двух параллельных прямых
Пустое множество- множество, не содержащее

ни одного элемента.

Что можно сказать о следующих множествах?

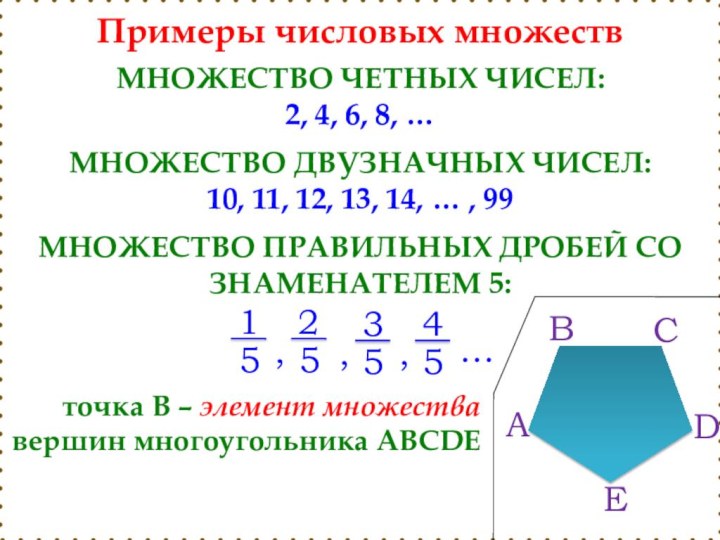
Слайд 5 Примеры числовых множеств
МНОЖЕСТВО ЧЕТНЫХ ЧИСЕЛ:
2, 4, 6, 8,

Примеры числовых множествМНОЖЕСТВО ЧЕТНЫХ ЧИСЕЛ:2, 4, 6, 8, …МНОЖЕСТВО ДВУЗНАЧНЫХ ЧИСЕЛ:10,

…
МНОЖЕСТВО ДВУЗНАЧНЫХ ЧИСЕЛ:
10, 11, 12, 13, 14, … ,

МНОЖЕСТВО ПРАВИЛЬНЫХ ДРОБЕЙ СО ЗНАМЕНАТЕЛЕМ 5:

…

точка В – элемент множества вершин многоугольника ABCDE

Слайд 6
N – множество натуральных чисел;

Z – множество целых чисел;
Q –

множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел;
С – множество комплексных чисел.

Числовые множества

Слайд 7 C

Слайд 8 Множество четырехугольников
Пространственные тела
1, 2, 3, 4, 5, 6,

Множество четырехугольниковПространственные тела1, 2, 3, 4, 5, 6, 7, 8, 9,

7, 8, 9, 10, 11…
Квадраты чисел
Цифры десятичной системы счисления
10,

12, 14, 16 … 96, 98

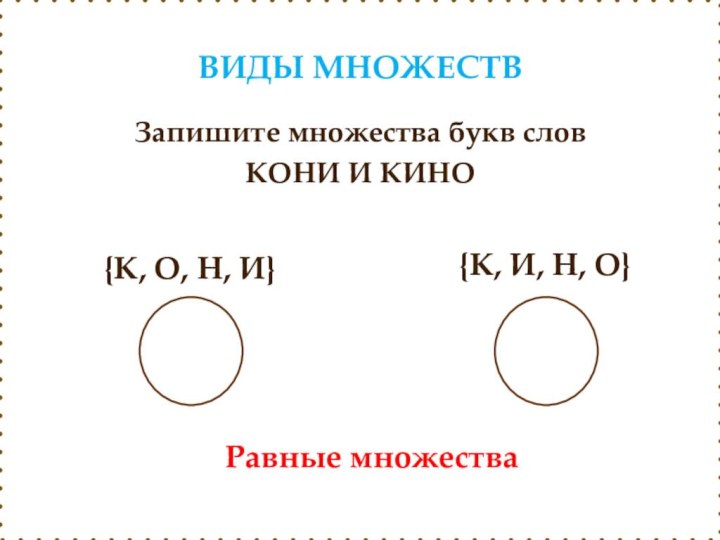
Слайд 9 ВИДЫ МНОЖЕСТВ
Запишите множества букв слов
КОНИ И КИНО
Равные

множества
{К, О, Н, И}
{К, И, Н, О}

Слайд 10 Даны множества:
М = {5, 4, 6},
Р

Даны множества: М = {5, 4, 6}, Р = {4, 5,

= {4, 5, 6},
Т = {5, 6, 7},

S = {4, 6}.

Какое из утверждений неверно?

а) М = Р б) Р ≠ S в) М ≠ Т г) Р = Т

Слайд 11 ВИДЫ МНОЖЕСТВ
А = {2; 3; 5; 7; 11;

13};

{х | 5< х

Слайд 12 ВИДЫ МНОЖЕСТВ
{1; 4; 9; 16; 25; …};

{10;

ВИДЫ МНОЖЕСТВ{1; 4; 9; 16; 25; …}; {10; 20; 30; 40;

20; 30; 40; 50; …};
Бесконечные множества

Слайд 13 Среди перечисленных ниже множеств укажите конечные

и бесконечные множества:
а) множество чисел, кратных 13;
б) множество

делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства
х + 1 < 3.

∞

Слайд 14 Основные способы задания множеств
1. Перечисление элементов. Элементы перечисляются

Основные способы задания множеств1. Перечисление элементов. Элементы перечисляются в фигурных скобках

в фигурных скобках через запятую.
2. С помощью характеристического свойства

(т.е. свойства, которым обладает каждый элемент множества и не обладает ни один элемент, ему не принадлежащий).

Слайд 15 ХАРАКТЕРИСТИЧЕСКОЕ СВОЙСТВО МНОЖЕСТВА – СВОЙСТВО, КОТОРЫМ ОБЛАДАЮТ ВСЕ

ХАРАКТЕРИСТИЧЕСКОЕ СВОЙСТВО МНОЖЕСТВА – СВОЙСТВО, КОТОРЫМ ОБЛАДАЮТ ВСЕ ЭЛЕМЕНТЫ ЭТОГО МНОЖЕСТВА

ЭЛЕМЕНТЫ ЭТОГО МНОЖЕСТВА И
НЕ ОБЛАДАЮТ НИКАКИЕ ДРУГИЕ ОБЪЕКТЫ.

Слайд 16 «МНОЖЕСТВО ВСЕХ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 1 ДО 14

«МНОЖЕСТВО ВСЕХ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 1 ДО 14 ВКЛЮЧИТЕЛЬНО» A={1, 2,

ВКЛЮЧИТЕЛЬНО»
A={1, 2, 3, 4, 5, 6, 7, 8,

9, 10, 11, 12, 13, 14}

«МНОЖЕСТВО ВСЕХ НАТУРАЛЬНЫХ ЧИСЕЛ МЕНЬШЕ 15»

«МНОЖЕСТВО ЗНАЧЕНИЙ X, ГДЕ X N И X < 15»

A = { X|X N, X < 15 }

Слайд 17 В – МНОЖЕСТВО НАТУРАЛЬНЫХ ЧИСЕЛ, КРАТНЫХ 5
5, 10,

В – МНОЖЕСТВО НАТУРАЛЬНЫХ ЧИСЕЛ, КРАТНЫХ 55, 10, 15, 20, 25,

15, 20, 25, …
В = { X|X=5n, n

N }

Слайд 18 C = { y|y=2x, x N, x

< 7 }
D = { 2, 4, 6, 8,

10, 12 }

C=D

{ 3, 4, 5, 6, 7 }

{ 5, 3, 7, 4, 6 }

Слайд 19 Задайте множество цифр, с помощью которых

Задайте множество цифр, с помощью которых записывается число: а) 3254;

записывается число:
а) 3254; б) 8797; в) 11000;

г) 555555.

Охарактеризуйте множество А:
а) А = {1, 3, 5, 7, 9};
б) А = {- 2, - 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};

Слайд 20 Отношения между множествами

Слайд 21 Множество В, каждый элемент которого принадлежит множеству А,

Множество В, каждый элемент которого принадлежит множеству А, называется подмножеством множества А. Например, множество

называется подмножеством множества А.

Например, множество всех чётных чисел является подмножеством множества

всех целых чисел.

Говорят, что множество А включает в себя множество В и обозначают А  В или В  А

Слайд 22

Слайд 23

Слайд 24 Суммой, или объединением множеств А и В называется

Суммой, или объединением множеств А и В называется множество, состоящее из

множество, состоящее из элементов, которые принадлежат хотя бы одному

из множеств А или В.
Объединение множеств обозначается

П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.

Слайд 25 ОБЪЕДИНЕНИЕ МНОЖЕСТВ

Слайд 26 Пересечением любого конечного или бесконечного множества множеств называется

Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из

множество, состоящее из тех и только тех элементов, которые

принадлежат этим множествам одновременно.
Пересечение множеств обозначается

П р и м е р : {1,2,3} {2,3,4} = {2,3}

Слайд 27 ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ

Слайд 28 Даны множества:
А = {2; 3; 8},

В = {2; 3; 8; 11},
С = {5;

11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.

Слайд 29 Даны множества:
А = {a, b, c,

d},
B = {c, d, e, f},
C =

{c, e, g, k}.
Найдите: (АUВ)UС.

Слайд 30 Даны множества:
А – множество всех натуральных чисел,

кратных 10,
В = {1; 2; 3;…, 41}.
Найдите А∩В.

Слайд 31 k
Решение задачи
с помощью кругов Эйлера
Леонард Эйлер

k Решение задачи с помощью кругов ЭйлераЛеонард Эйлер — швейцарский, немецкий

— швейцарский, немецкий и российский математик, внёсший значительный вклад

в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

Слайд 32 поют 17
танцуют 19
Всего 30
17+19=36, всего 30
36-30=6
6
11
13
В классе 30

поют 17танцуют 19Всего 3017+19=36, всего 3036-30=661113В классе 30 человек, каждый из

человек, каждый из которых поёт или танцует. Известно, что

поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?

Слайд 33 Всего 67
Английский 47
Немецкий 35
23
47-23=24
24
35-23=12
12
24+12+23=59
67- 59=8

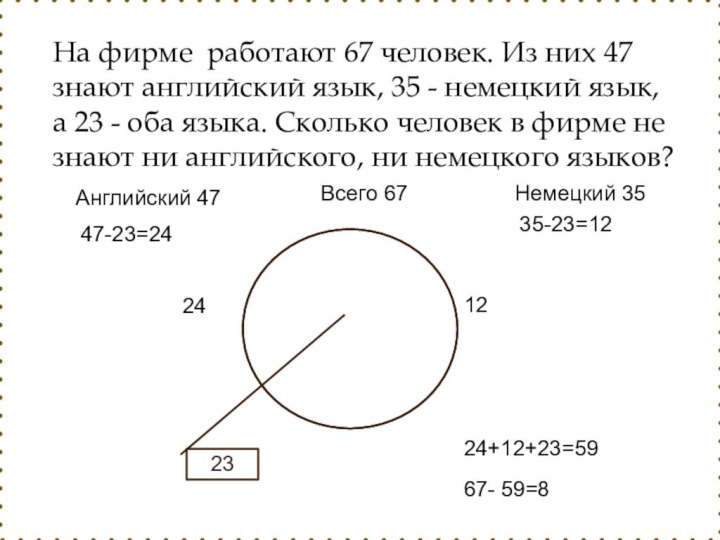
На фирме работают 67

Всего 67Английский 47Немецкий 352347-23=242435-23=121224+12+23=5967- 59=8На фирме работают 67 человек. Из них

человек. Из них 47 знают английский язык, 35 -

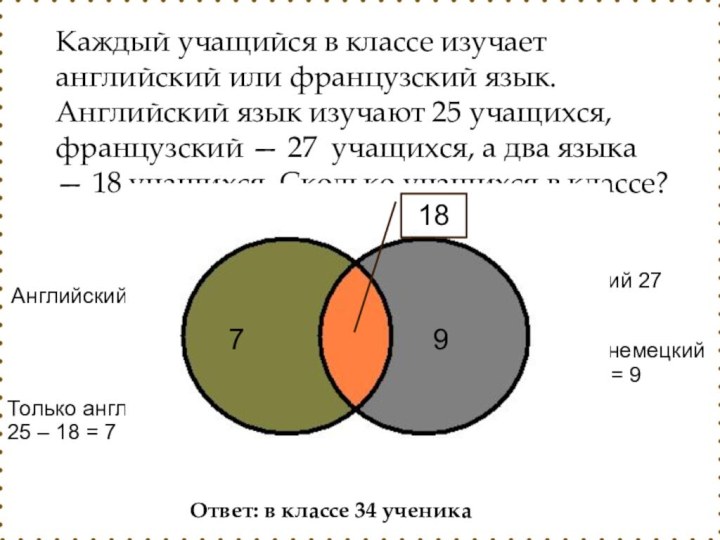
немецкий язык, а 23 - оба языка. Сколько человек в фирме не знают ни английского, ни немецкого языков?

Слайд 34 Каждый учащийся в классе изучает английский или французский

Каждый учащийся в классе изучает английский или французский язык. Английский язык

язык. Английский язык изучают 25 учащихся, французский — 27

учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?

Ответ: в классе 34 ученика

Английский 25

Немецкий 27

Только английский
25 – 18 = 7

Только немецкий
27 – 18 = 9

7 + 9 + 18 = 34

Слайд 35 Расположите 4 элемента в двух множествах так, чтобы

в каждом из них было по 3 элемента.

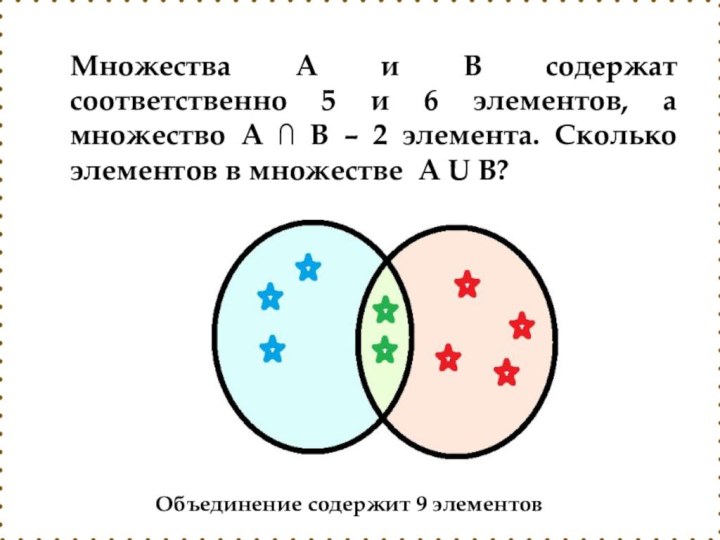
Слайд 36 Множества А и В содержат соответственно 5 и

Множества А и В содержат соответственно 5 и 6 элементов, а

6 элементов, а множество А ∩ В – 2

элемента. Сколько элементов в множестве А U В?

Объединение содержит 9 элементов

Слайд 37 Каждая семья, живущая в нашем доме, выписывает или

Каждая семья, живущая в нашем доме, выписывает или газету, или журнал,

газету, или журнал, или и то и другое вместе.

75 семей выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?

Всего: 14 + 13 + 62 =89

Слайд 38 Задачи для самостоятельного решения

Слайд 39 На школьной спартакиаде каждый из 25 учеников 9

На школьной спартакиаде каждый из 25 учеников 9 –го класса выполнил

–го класса выполнил норматив или по бегу, или по

прыжкам в высоту.
Оба норматива выполнили 7 человек, а 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту.
Сколько учеников выполнили норматив:
а) по бегу;
б) по прыжкам в высоту;
в) по прыжкам при условии, что не выполнен норматив по бегу?