его модулем называется само число, если оно неотрицательно, и
– ему противоположное, если число отрицательное
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть










![Презентация по математике на тему Построение графиков функций с модулем y=|x-2|x-2=0, отсюда x=2Будем рассматривать два интервала (-∞;2] и [2;∞)При x](/img/tmb/7/618893/f284a7ad064bbc10ead8daa2735d15af-720x.jpg)
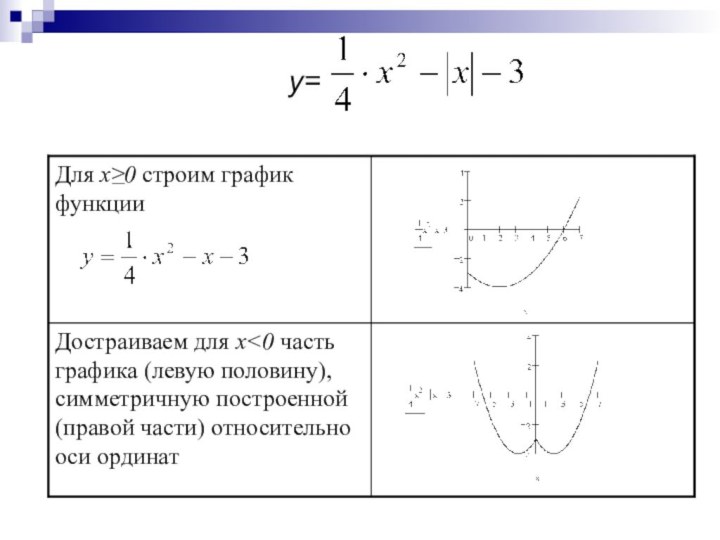
![Презентация по математике на тему Построение графиков функций с модулем y=x2-3|x|+2 x=0Будем рассматривать следующие интервала (-∞;0] и [0;∞)При x](/img/tmb/7/618893/192c19876ecf4bf3da09b486da515150-720x.jpg)


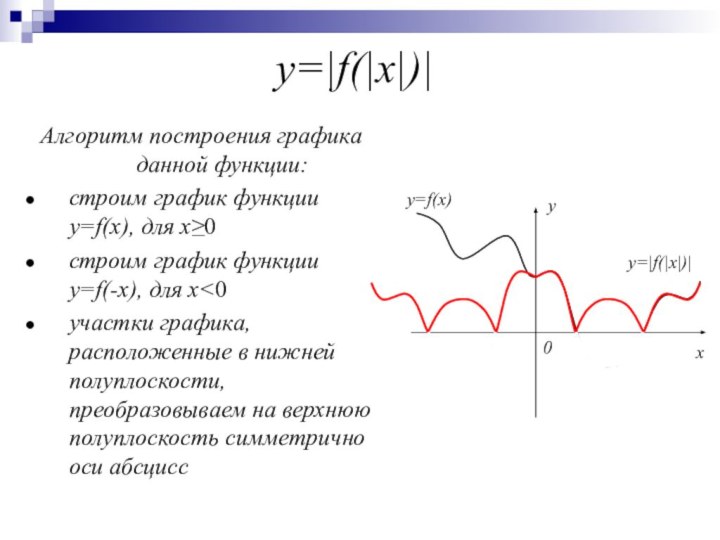
x
y
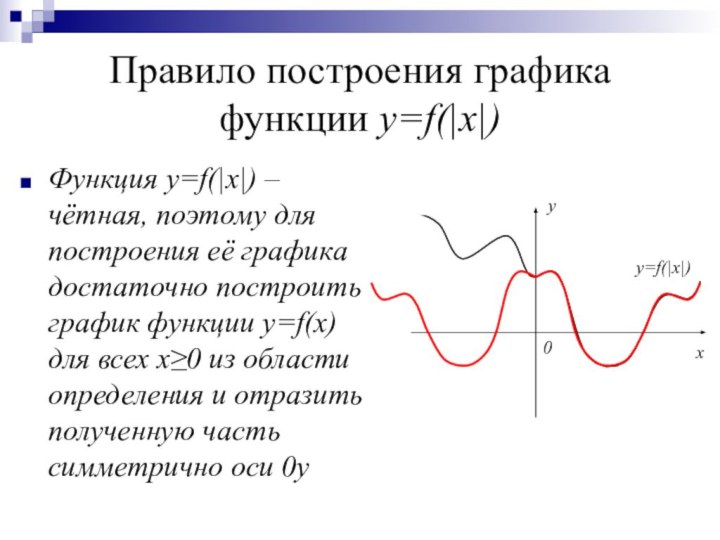
y=f(x)
y=f(|x|)
0
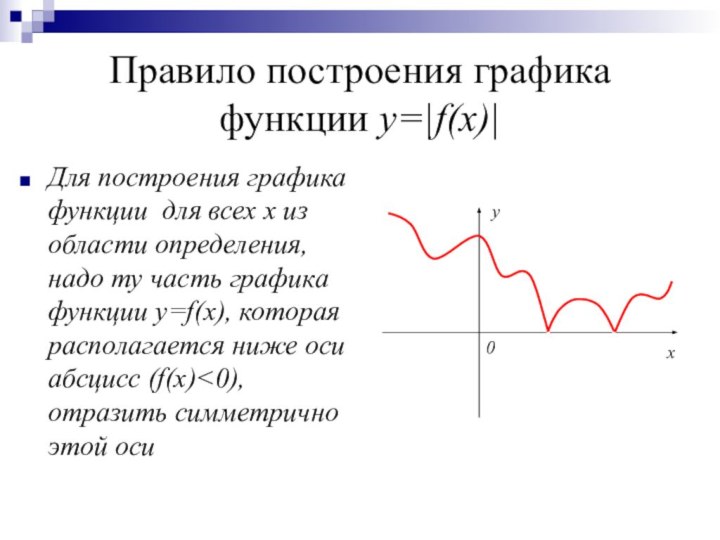
y=f(x)
y=|f(x)|
x
y
0
x
y
y=f(x)
y=f(|x|)
y=|f(|x|)|
y=|f(|x|)|
0
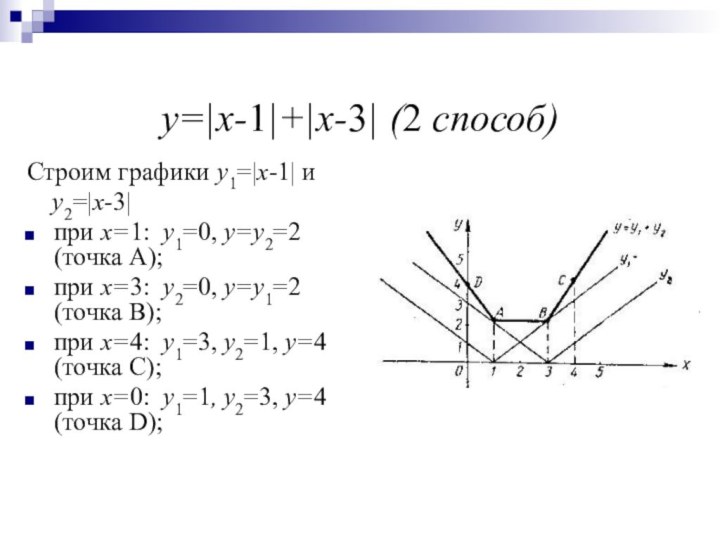
2) путём сложения ординат графиков функций
,…
соответствующих одним и тем же абсциссам.