- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике Софизмы в математике
Содержание
- 2. Эпиграф В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками. И. Ньютон
- 3. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибокГипотеза
- 4. Цель:Задачи:Цель и задачиНаучиться распознавать софизмы и обнаруживать
- 5. Софизм - (от греческого sophisma –
- 6. Из истории софизмов Сократ469 – 399
- 7. ЕвклидОколо 365 — 300 до н. э.«Псевдарий»
- 8. «Сколько людей, столько и мнений»«Истина едина для всех»СофистыСократистыАристотельСократ
- 9. Вторая софистика Дион Прусский170 – 247 г.Лукиан120-
- 10. КлассификацияМатематические софизмыАрифметическиеАлгебраические
- 11. Дважды два – пять.Доказательство:Пусть исходное соотношение
- 12. «Единица равна нулю»Доказательство:Возьмем уравнение
- 13. Геометрические софизмы«Катет равен гипотенузе»∠С = 90˚, ВД
- 14. Доказательство:Полупустое есть то же, что и
- 15. «Когда же учиться?»1. По ночам занятий нет, половина
- 16. Результаты исследования1.Доводилось ли вам слышать подобную фразу:
- 17. 3.Надо ли знакомить учащихся на уроках с софизмами?4.Хотел бы ты больше узнать софизмов?
- 18. Найдите ошибку 1. Чётное и
- 19.
- 20. Сборник заданий
- 21. ВыводыСофистика – целая наука, а математические софизмы
- 22. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибокГипотеза
- 23. 1. Д.Я. Стройк Краткий очерк истории математики.-М.:Наука,1978.
- 24. Скачать презентацию
- 25. Похожие презентации























Слайд 3
Каким бы ни был софизм,
он всегда содержит
одну или несколько замаскированных ошибок
Гипотеза
Слайд 4
Цель:
Задачи:
Цель и задачи
Научиться распознавать софизмы и обнаруживать ошибки,
чтобы не допустить ложного решения.
- изучить понятие софизмов;
- выявить
недостатки в истолковании софизмов;- выяснить, какие бывают софизмы в математике;
- выяснить, какие основные ошибки допускаются в математических софизмах;
- выявить роль софизмов в математике.
Слайд 5 Софизм - (от греческого sophisma – уловка,
ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую
нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям.Софизмы
Слайд 6
Из истории софизмов
Сократ
469 – 399 г.
до н. э.
.
Платон
428 – 348 г.
до н. э.Аристотель
384 – 322 г. до н.э
Слайд 9
Вторая софистика
Дион Прусский
170 – 247 г.
Лукиан
120- 180
г.
Герод Аттик
101 – 177 г
Филострат
ок. 178 ок. 248 гг
Слайд 11
Дважды два – пять.
Доказательство:
Пусть исходное соотношение -
очевидное равенство:
4:4 = 5:5 (1) Вынесем за скобки общий множитель каждой части
равенств (1) , и мы получим:
4 ∙ (1:1)=5∙(1:1) (2)
Разложим число 4 на произведение 2∙2:
(2∙2)∙ (1:1)=5∙(1:1) (3)
Наконец, зная, что 1:1=1, мы из соотношения (2)
устанавливаем: 2∙2=5.
Арифметические софизмы
4 ∙ (1:1)=5∙(1:1)
2*2=5
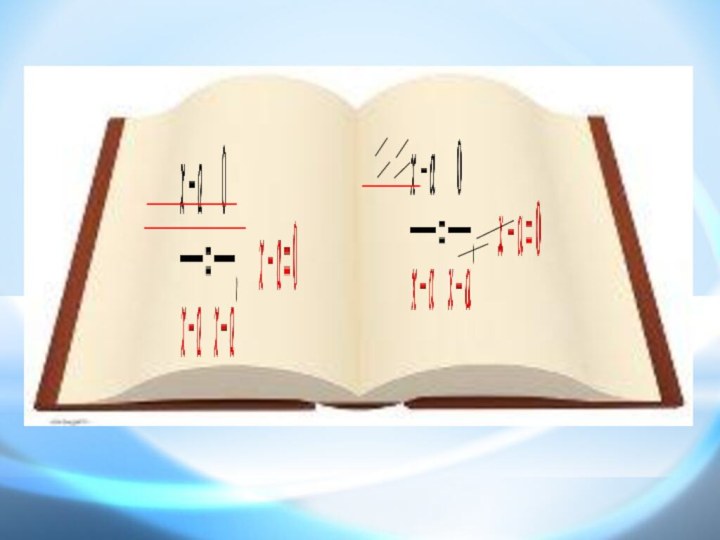
Слайд 12
«Единица равна нулю»
Доказательство:
Возьмем уравнение
x-a = 0
Разделив обе его части на
х-а, получим Откуда сразу же получаем требуемое равенство 1=0
Алгебраические софизмы
Ошибка:
1 = 0
Слайд 13
Геометрические софизмы
«Катет равен гипотенузе»
∠С = 90˚, ВД -
биссектриса ∠СВА, СК = КА,
ОК ⊥ СА,
О -
точка пересечения прямых ОК и ВД, ОМ ⊥ АВ, ОL ⊥ ВС.
Имеем: Δ LВО = Δ МВО, ВL = ВМ,
ОМ = ОL = СК = КА,
КОА = Δ ОМА (ОА - общая сторона, КА = ОМ,
∠ ОКА и ∠ ОМА - прямые),
∠ ОАК = ∠ МОА, ОК = МА = СL, ВА = ВМ + МА,
ВС = ВL + LС, но ВМ = ВL, МА = СL,
и потому ВА = ВС.
о
о
Слайд 14
Доказательство:
Полупустое есть то же, что и полуполное.
Если равны половины,
значит, равны и целые.
Следовательно, пустое есть
то же, что и полное.Логические софизмы
«Полупустое и полуполное»
Слайд 15
«Когда же учиться?»
1. По ночам занятий нет, половина суток
свободна. Остаётся:
365-182=183 дня. 2. В школе ученики занимаются половину дня, значит, вторая половина (или четвёртая часть суток) может быть свободна. Остаётся: 183-183:4=137 дней. 3. В году 52 воскресенья. Из них на каникулы приходится 15 дней, таким образом, выходных в учебном году 52-15=37 дней. Итого остаётся 137-37=100 дней. 4. Есть ещё каникулы: осенние (5 дней), зимние (10 дней), весенние (7 дней), летние (78 дней). Всего 5+10+7+78=100 дней. 5. Итак, школьники заняты в году 100-100=0 дней. Когда же учиться?!Логические софизмы
Слайд 16
Результаты исследования
1.Доводилось ли вам слышать подобную фразу: «Дважды
два равно пяти» или хотя бы: «Два равно трем»?
2.Знакомо
ли вам понятие «Софизм»?
Слайд 18
Найдите ошибку
1. Чётное и нечётное
5 есть 2 + 3 («два и три»)
Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное. Пять не делится на два, также, как и 2 + 3, значит, оба числа нечётные. Где ошибка?2. 5 = 6
Попытаемся доказать, что 5 = 6.
С этой целью возьмем числовое тождество: 35+10-45=42+12-54 .
Вынесем общие множители левой и правой частей за скобки.
Получим: 5(7+2-9) = 6(7+2-9) .
Разделим обе части этого равенства на общий множитель (заключенный в скобки).
Получаем 5 = 6.
В чем ошибка?
3. 5 = 1
Желая доказать, что 5 = 1, будем рассуждать так.
Из чисел 5 и 1 по отдельности вычтем одно и то же число 3. Получим числа 2 и -2 . При возведении в квадрат этих чисел получаются равные числа 4 и 4. Значит, должны быть равны и исходные числа 5 и 1. Где ошибка?
Слайд 21
Выводы
Софистика – целая наука, а математические софизмы –
это часть большого течения.
Разбор софизмов развивает логическое мышление.
Исследовать софизмы
интересно и необычно.Разбор софизмов увлекателен.
Математические софизмы заставляют внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записей и чертежей, за допустимостью обобщений, за законностью выполняемых операций.
Благодаря софизмам можно научиться искать ошибки в рассуждениях других.
Слайд 22
Каким бы ни был софизм,
он всегда содержит
одну или несколько замаскированных ошибок
Гипотеза
Слайд 23
1. Д.Я. Стройк Краткий очерк истории математики.-М.:Наука,1978.
2. Ф.Ф.Нагибина, Е.С.Канина Математическая шкатулка: Пособие
для учащихся 4-8 кл.средн.шк. –М.: Просвещение, 1988. 3. А.Г.Мадера, Д.А.Мадера Математические софизмы. – М.:
Просвещение,2003.
С.И.Ожегова, Н.Ю. Шведова Толковый словарь русского языка-
М.: ООО «ИТИ Технологии», 2006.
Сайты Интернет:
5. http://sofizmy.narod.ru
Список использованной литературы