- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Индивидуальный проект на тему “Построение сечений”
Содержание
- 2. Определение Секущая плоскость – любая плоскость по обе стороны которой имеются точки
- 3. Цель.Наша задача – решить задачи на построение сечений и показать решение на макете.
- 4. Задача 1.Дан тетраэдр АВСD. Точка M принадлежит ребру тетраэдра АВ, точка N
- 5. Ответ на задачу 1.Рассмотрим грань тетраэдра DВС. В
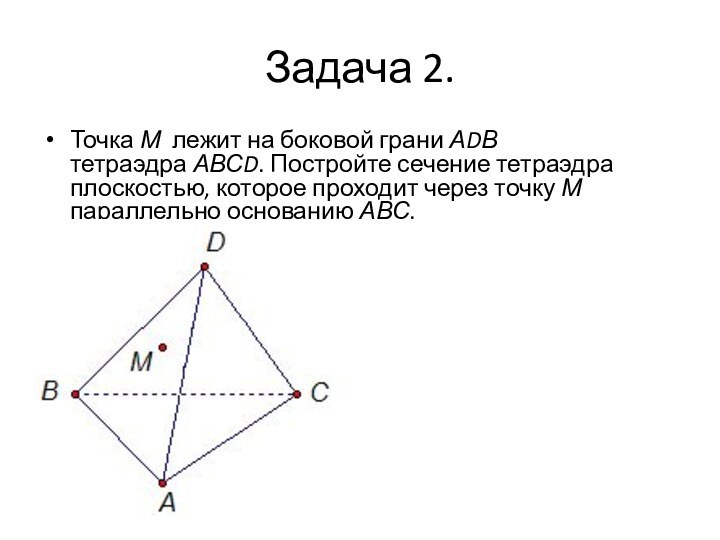
- 6. Задача 2.Точка М лежит на боковой грани АDВ тетраэдра АВСD.
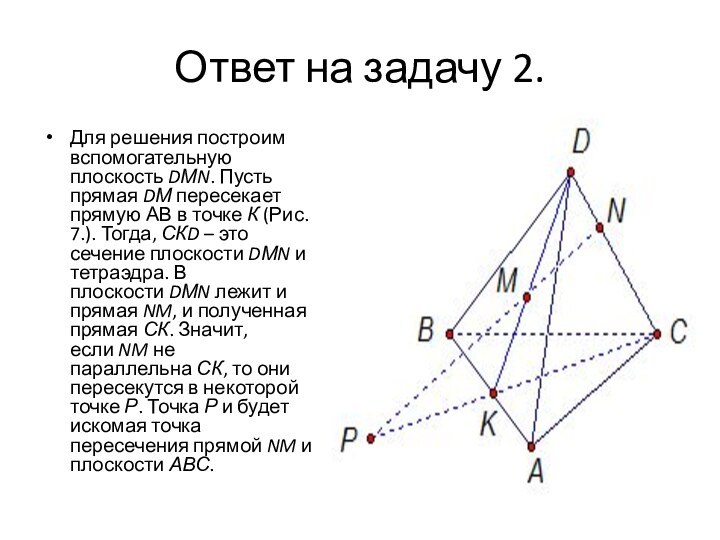
- 7. Ответ на задачу 2.Для решения построим вспомогательную
- 8. Задача 3.Дан тетраэдр АВСD. М – внутренняя точка грани АВD.
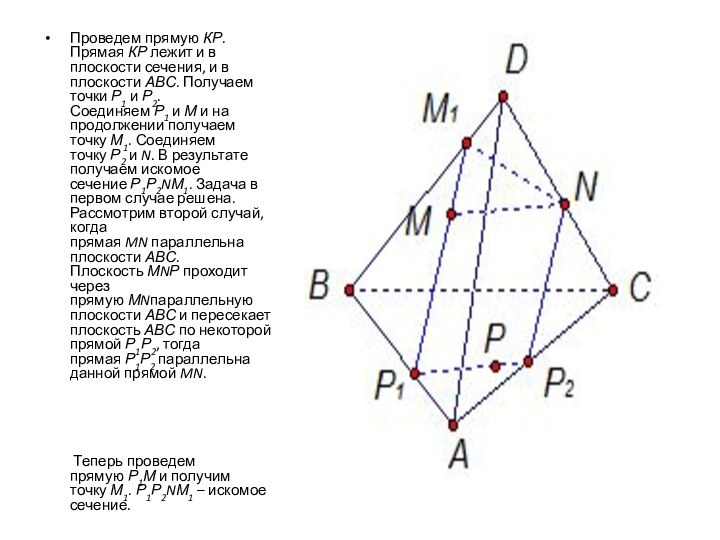
- 9. Решение задачи 3.Рассмотрим первый случай, когда прямая MN не
- 10. Скачать презентацию
- 11. Похожие презентации
Определение Секущая плоскость – любая плоскость по обе стороны которой имеются точки





Слайд 4
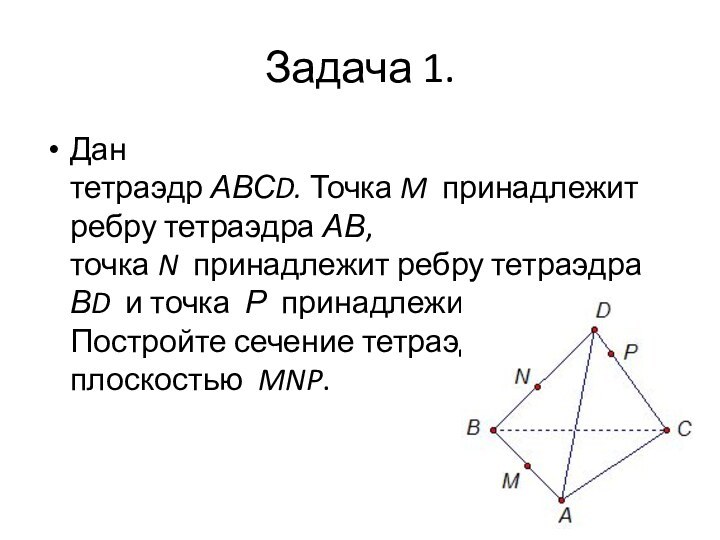
Задача 1.
Дан тетраэдр АВСD. Точка M принадлежит ребру тетраэдра АВ, точка N принадлежит
ребру тетраэдра ВD и точка Р принадлежит ребру DС. Постройте
сечение тетраэдра плоскостью MNP.
Слайд 5
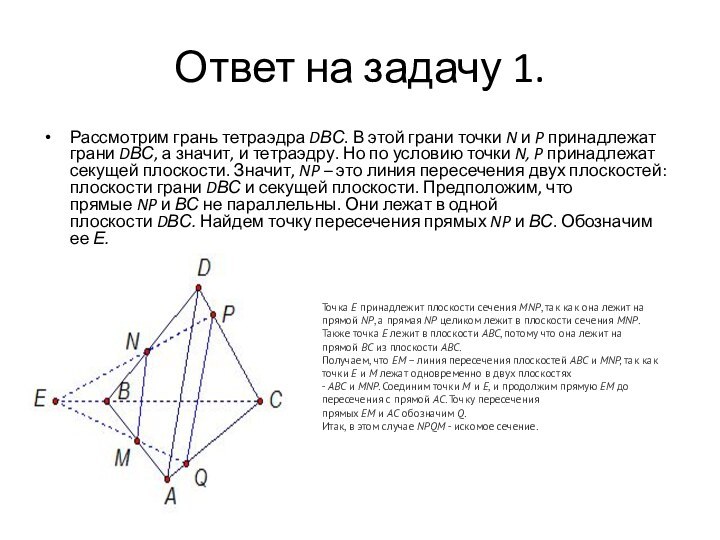
Ответ на задачу 1.
Рассмотрим грань тетраэдра DВС. В этой
грани точки N и P принадлежат грани DВС, а значит, и тетраэдру. Но по
условию точки N, P принадлежат секущей плоскости. Значит, NP – это линия пересечения двух плоскостей: плоскости грани DВС и секущей плоскости. Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости DВС. Найдем точку пересечения прямых NP и ВС. Обозначим ее Е.Точка Е принадлежит плоскости сечения MNP, так как она лежит на прямой NР, а прямая NР целиком лежит в плоскости сечения MNP.
Также точка Е лежит в плоскости АВС, потому что она лежит на прямой ВС из плоскости АВС.
Получаем, что ЕМ – линия пересечения плоскостей АВС и MNP, так как точки Е и М лежат одновременно в двух плоскостях - АВС и MNP. Соединим точки М и Е, и продолжим прямую ЕМ до пересечения с прямой АС. Точку пересечения прямых ЕМ и АС обозначим Q.
Итак, в этом случае NPQМ - искомое сечение.





























