- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку Призма
Содержание
- 2. -ТЕОРИЯ - ЭЛЕМЕНТЫ
- 3. Призма (греч. prísma), многогранник, у которого две
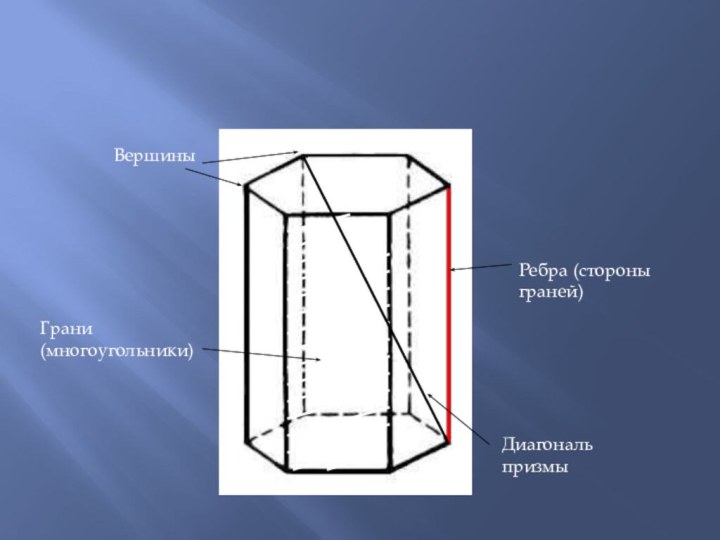
- 4. ВершиныГрани (многоугольники)Ребра (стороны граней)Диагональ призмы
- 5. Высотой (h) призмы называется перпендикуляр , опущенный
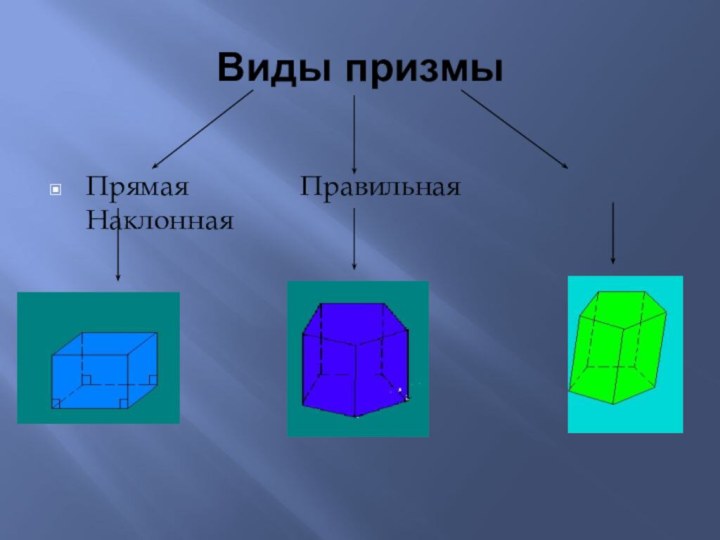
- 6. Виды призмыПрямая
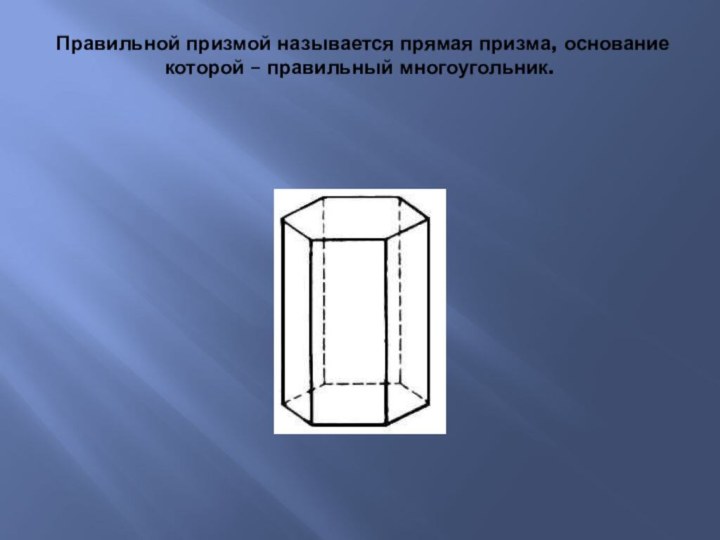
- 7. Правильной призмой называется прямая призма, основание которой – правильный многоугольник.
- 8. Площадь поверхности призмы (Sпр) равна сумме
- 9. Площадь боковой поверхности – сумма площадей боковых
- 10. Объём прямой призмы, основанием которой является
- 11. Параллелепипедом называется призма, основание которой –
- 12. Противоположные грани параллелепипеда равны параллельны Все
- 13. Применение призмы в архитектуре
- 14. Применение призмы в быту
- 15. Скачать презентацию
- 16. Похожие презентации
-ТЕОРИЯ - ЭЛЕМЕНТЫ - НАХОЖДЕНИЕ ПЛОЩАДЕЙ - НАХОЖДЕНИЕ ОБЪЕМА - ПРИМЕНЕНИЕ ПРИЗМЫ


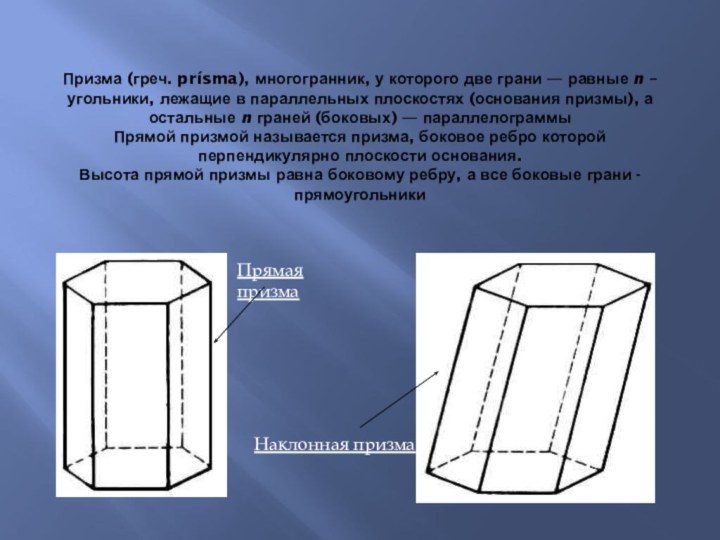




Слайд 3 Призма (греч. prísma), многогранник, у которого две грани
— равные n –угольники, лежащие в параллельных плоскостях (основания
призмы), а остальные n граней (боковых) — параллелограммы Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна боковому ребру, а все боковые грани - прямоугольникиПрямая призма
Наклонная призма
Слайд 5 Высотой (h) призмы называется перпендикуляр , опущенный из
любой точки одного основания на плоскость другого основания призмы.
Отрезок,
концы которого - две вершины, не принадлежащие одной грани призмы,
называют ее диагональю.
(Отрезок A1D - диагональ призмы)
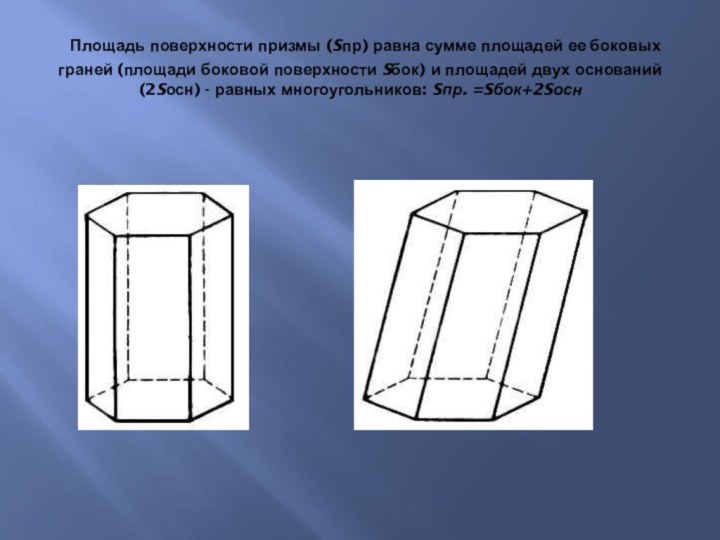
Слайд 8 Площадь поверхности призмы (Sпр) равна сумме площадей
ее боковых граней (площади боковой поверхности Sбок) и площадей
двух оснований (2Sосн) - равных многоугольников: Sпр. =Sбок+2SоснСлайд 9 Площадь боковой поверхности – сумма площадей боковых граней
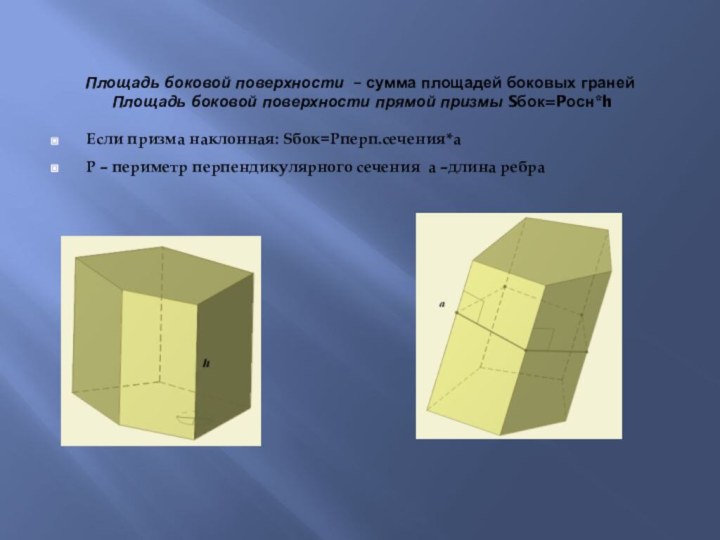
Площадь боковой поверхности прямой призмы Sбок=Pосн*h
Если призма наклонная:
Sбок=Pперп.сечения*aP – периметр перпендикулярного сечения a –длина ребра
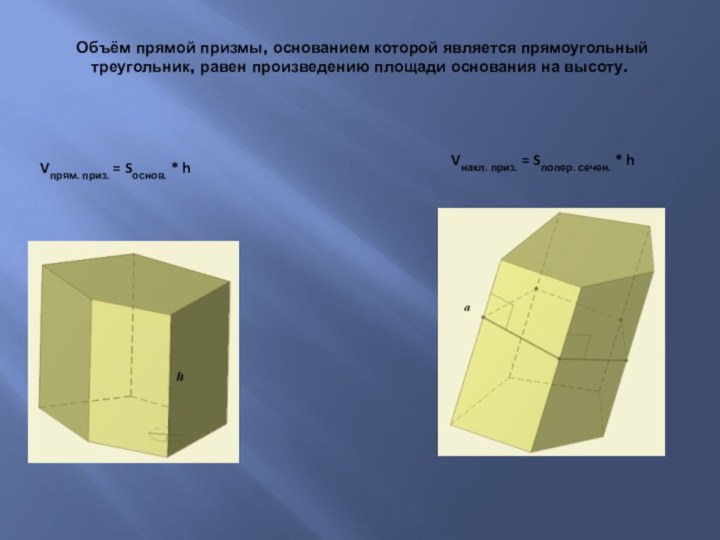
Слайд 10 Объём прямой призмы, основанием которой является прямоугольный
треугольник, равен произведению площади основания на высоту.
Vпрям. приз. =
Sоснов. * hVнакл. приз. = Sпопер. сечен. * h
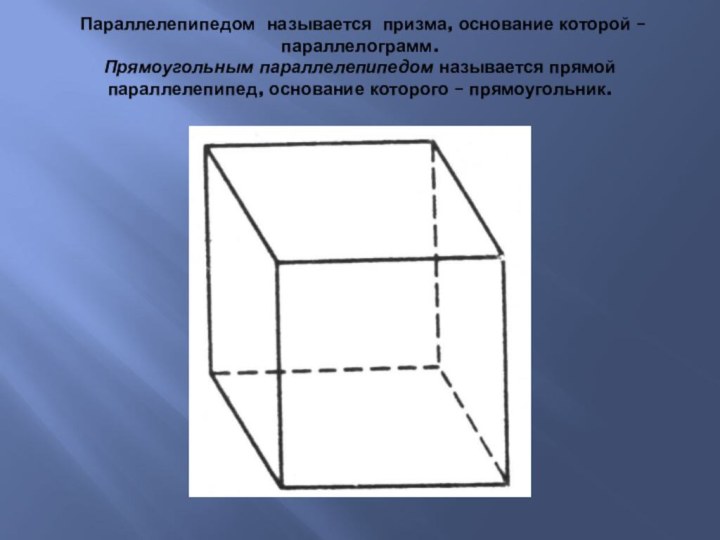
Слайд 11 Параллелепипедом называется призма, основание которой – параллелограмм. Прямоугольным
параллелепипедом называется прямой параллелепипед, основание которого – прямоугольник.
Слайд 12
Противоположные грани параллелепипеда равны параллельны
Все четыре
диагонали параллелепипеда пересекаются в одной точке и делятся этой
точкой пополам.Сумма квадратов диагоналей параллелепипеда равна сумме квадратов всех его ребер.
Боковые грани прямого параллелепипеда – прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.