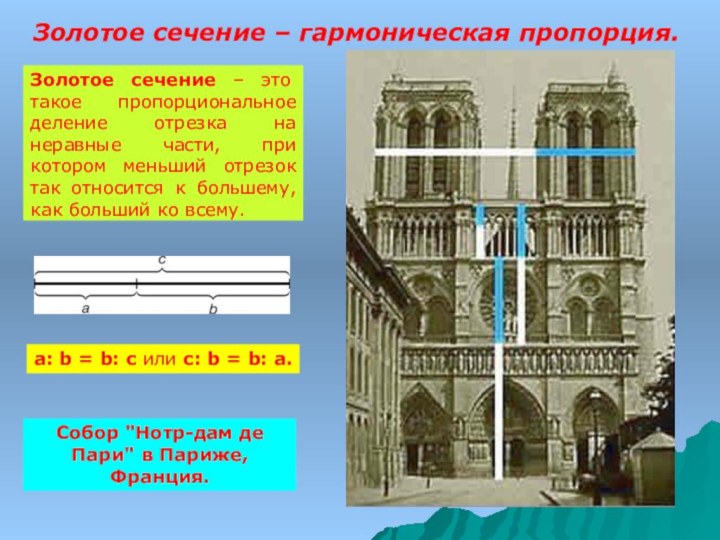
ряд
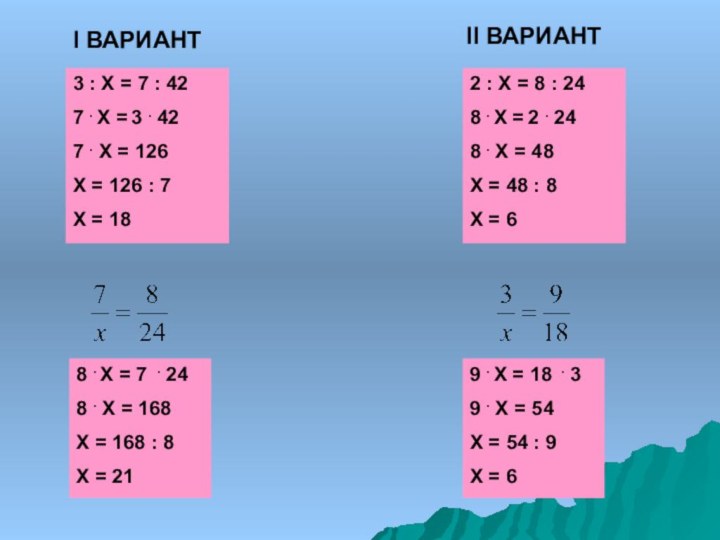
28:7=16:4
В верной пропорции произведение крайних членов равно произведению средних.
Если произведение крайних членов равно произведению средних, то пропорция верна